基于复数微分算子的最优化分解方法及其应用

孟祥晶，程军圣，杨 宇，潘海洋

(湖南大学 汽车车身先进设计制造国家重点实验室，长沙410082)

在机械故障诊断的研究领域中，目前的研究热点是选择合适的信号处理方法完成对设备振动信号的分析。常见的方法有短时傅里叶变换（Short-Time Fourier Transform，简 称STFT）[1]、小 波 变 换(Wavelet Transform，简称WT)[2]、经验模态分解（Empirical Mode Decomposition，简称EMD）[3–4]以及由EMD 衍生出的局部特征尺度分解（Local Characteristic scale Decomposition，简称LCD）方法和局部均值分解（Local Mean Decomposition，简称LMD）方法等。上述信号分析与处理方法均在机械振动信号处理方面得到了广泛的应用并取得了较好的效果[5–7]。

STFT和WT作为早期的信号分析方法，通常受到固定基函数的制约，往往使得分解的结果不具有物理意义，从而不能够有效提取混合信号的最本质特征。EMD 及其衍生算法是近期最具代表性的信号分析方法，但是仍存在端点效应及模态混叠等缺点。鉴于以往信号处理方法的不足及信号的非线性特点，Thomas 等提出了自适应最稀疏时频分析（Adaptive Sparsest Time Frequency Analysis,简 称ASTFA）[8]方法。其主要思想是在包含内禀模态函数（Intrinsic Mode Functions，简称IMF）[9]的过完备字典库中搜索信号的最稀疏解，将混合信号的分解问题转变为获得单分量个数最少的优化问题。ASTFA无需选取基函数，分解得到的每个分量都可以表示为一个包络函数和一个余弦函数的乘积，相比STFT和WT 的分析结果更有物理意义，且在优化过程中抑制了端点效应和模态混淆。但是ASTFA 仍存在一些不足，如包络函数比余弦函数更平滑是分量的约束条件，实际的包络函数和余弦函数成分有可能发生交叠，致使分解结果受到影响。另外，ASTFA需要对信号的所有数据点进行优化，优化参数过多导致计算量变大。

针对ASTFA方法的不足，本文提出基于复数微分算子的最稀疏分解（Optimization Decomposition Based on Complex Differential Operators，简 称CDOOD）方法。CDOOD 的实质是对原始信号进行滤波，即设计滤波器χ(k|λ)，然后对其参数λ进行优化，以便获得信号的最优化解。由于使用了滤波器，CDOOD 需要优化的参数个数远远小于ASTFA，因此该方法极大地减少了计算量。此外，CDOOD 约束条件为使得单分量满足局部窄带信号[10]的条件，与ASTFA相比较，克服了包络函数和余弦函数成分有可能发生交叠而导致分量的物理意义不明确的缺点。

综上所述，本文提出了CDOOD方法，并介绍其基本原理。首先建立适合非线性与非平稳信号的滤波器，其次根据滤波后的信号产生复数微分算子并将分量约束为局部窄带信号，最后通过优化算法寻找目标函数的最优化解。使用仿真信号进行分析，结果表明了CDOOD 方法不但克服了EMD 在分解环节中出现的端点效应与模态混叠的缺点，也克服了ASTFA出现端点效应的缺点，并且在准确性和正交性方面具有优越性。使用CDOOD方法对齿轮与轴承复合故障进行诊断分析，结果表明该信号分解方法在旋转机械复合故障诊断中，相比于EMD 和ASTFA，能够更准确地提取故障特征。

1 CDOOD方法原理

CDOOD 方法的主要思想是通过优化滤波器参数将混合信号的分解问题转变为非线性优化问题，优化目标为使得分解的余量的能量最小，约束条件为使得单分量满足局部窄带信号的条件，最终优化分解为若干个内禀窄带分量。其分解步骤如下：

(1) 选择一时域信号s(t)，同时令si(t)=s(t)（si(t)是每次迭代的初始输入信号）；

(2) 对si(t)进行快速傅里叶变换，得到si(k)=fft(si(t))，si(k)的快速傅里叶逆变换为si(t)=ifft(si(k))；

(3)建立滤波器χ(k|λ)，其中λ=[ω,ωb,ωc]，由于使用遗传算法优化滤波器参数，并且随机生成初始种群，故ω、ωb与ωc随机产生

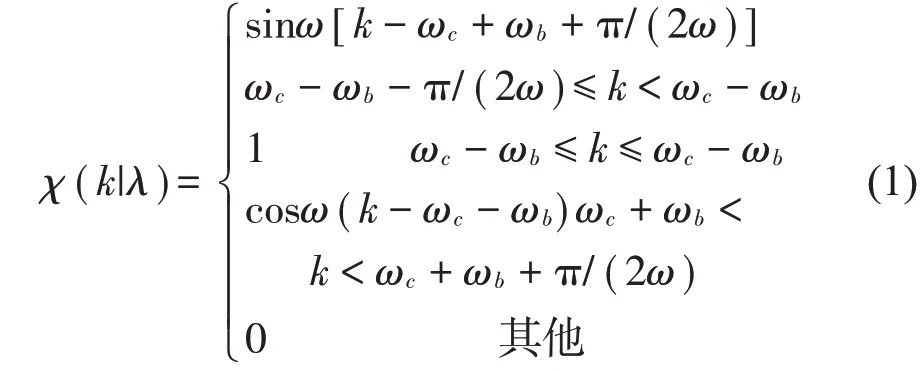
通过步骤(3)获得具有一定特征的滤波信号，同时建立了完备字典库Dic

符合式（2）条件的称之为窄带信号。假设一个窄带信号的任意一个时间点上都存在一个临域区间，使得信号在此区间满足过完备字典库的条件，那么这个信号就被称作局部窄带信号，本文称其为内禀窄带分量（Intrinsic Narrow-Band Components，简称INBC）。

(5)利用遗传算法解决如下的最优化问题：

利用步骤(4)中的复数微分算子使内禀窄带分量在式（3）中为零[11]，进而得到最优化参数λ0，之后令INBCi=ifft[χ(k|λ0)si(k)]；得到一个内禀窄带分量。

(6) 为了继续得到内禀窄带分量，令si+1=si-INBCi；

(7)若||si+1||2<ξ，则分解终止，否则令i=i+1并返回第二步，直至得到所有的内禀窄带分量。

2 仿真信号对比分析

考虑如下的仿真信号

图1 CDOOD方法流程图

其中x1(t)是调幅调频信号，x2(t)是简单的正弦信号。混合信号x(t)的采样频率1 024 Hz，采样时间为1 s。x(t)及其分量的波形图如图2所示。

图2 混合信号及其分量的波形图

为了说明CDOOD 时频分析方法的分解性能，对仿真混合信号x(t)分别采用EMD、ASTFA 与CDOOD进行分解，分解结果如图3至图5所示。由图2 至图5 的分解结果可知，经过EMD 的分解可以得到4 个主要的IMF 分量，IMF1和IMF2中包含了原信号的主要能量，但仿真信号中的x1(t)、x2(t)并未被分解开来，其分解效果不明显，端点效应严重。ASTFA分解结果出现了明显的端点效应，并且分解的残余较大，能量泄露严重。相比EMD和ASTFA，CDOOD的分解结果更加平滑，残余更小且无明显的能量泄露和端点效应。由此可以看出CDOOD 能更有效抑制端点效应且分解效果更好。

图3 混合信号基于EMD的分解结果

图4 混合信号基于ASTFA的分解结果

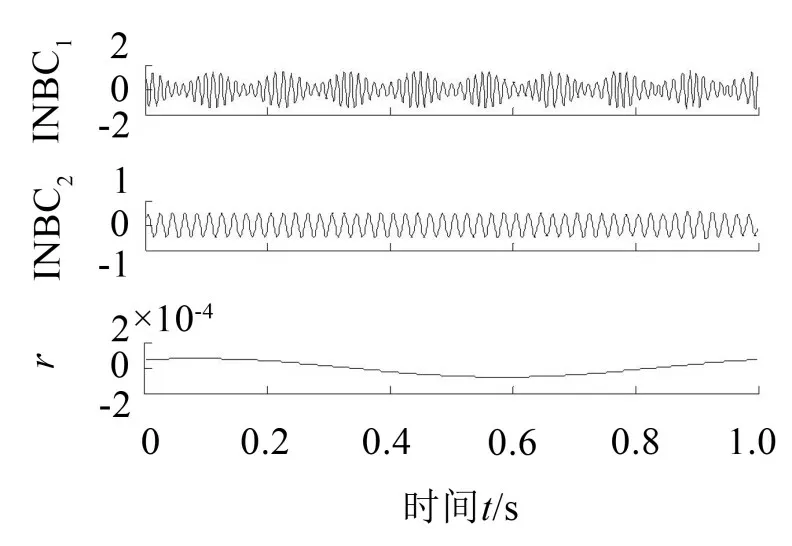
图5 混合信号基于CDOOD的分解结果

另外，为了直观观察各分解方法的分解效果，分别作出各分量的误差曲线，如图6 所示。可以看出，ASTFA 的误差小于EMD，CDOOD 的误差小于ASTFA，说明了CDOOD 方法的分解能力强于ASTFA和EMD。

为了进一步量化比较CDOOD、ASTFA及EMD 3 种方法的分解能力，分别使用能量误差Ei和相关系数ri[12]考察分解分量与真实分量的吻合程度；使用正交性指标IO考察3种方法的正交性。具体数值如表1所示。

由表1 可以看出，相比于EMD 和ASTFA，CDOOD 的分解分量与真实分量的能量误差更小，相关系数更高，正交性指标更小，说明了CDOOD的分解能力确实强于EMD和ASTFA。

图6 基于EMD、ASTFA、CDOOD的信号分解结果各分量误差曲线

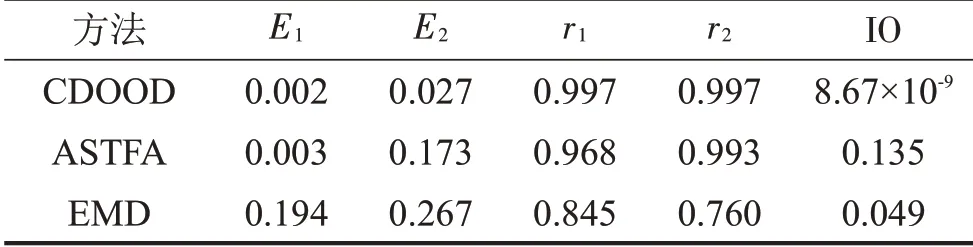
表1 基于CDOOD、ASTFA、EMD 3种方法的分解结果评价指标比较

3 齿轮箱复合故障诊断实验分析

为了验证CDOOD 在实际应用中的可行性，将所提方法用于湖南大学试验故障台采集的机械复合故障数据中。该试验通过激光切割，在轴承和齿轮上模拟混合故障。滚动轴承的型号为SKF6307-2RS，在轴承的外圈上切割宽0.15 mm、深0.2 mm 的槽。齿轮的齿数为37，在齿轮上切掉一个齿。至此齿轮箱复合故障设置完毕。实验中通过将加速度传感器放置于合适的位置来采集振动信号，采样频率为fs=8 192 Hz，采样时间为1 s。滚动轴承与齿轮所在轴的转速为600 r/min，即转频为fr=10 Hz，经过计算，滚动轴承出现外圈故障时的特征频率约为fo=31 Hz。

将采集到的齿轮箱复合故障信号（如图7所示）进行包络谱分析，得到的结果如图8所示。

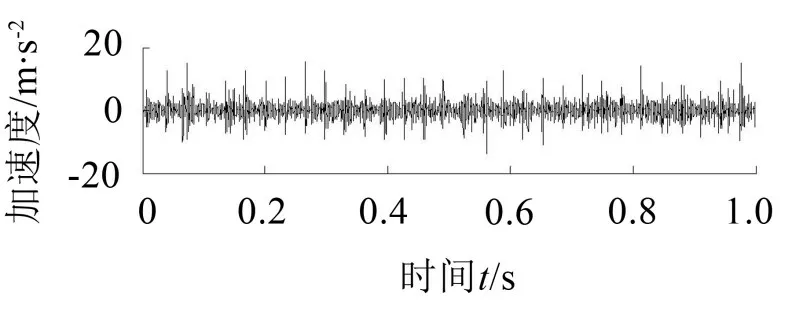
图7 复合故障信号时域波形图

图8 复合故障信号包络谱

从其包络谱可以分析出，复合故障信号中的轴承故障特征频率及其2 倍频、3 倍频等明显，说明轴承故障被成功提取出来，但是齿轮故障特征频率被其它信号的所淹没，无法判断齿轮是否发生故障。

对复合故障振动信号进行EMD、ASTFA 和CDOOD分解，分解的结果分别如图9至图11所示。

图9 EMD分量的时域波形图

图10 ASTFA分量的时域波形图

图11 CDOOD分量的时域波形图

使用包络谱分析方法对分解后所得分量进行解调，如图12至图14所示。

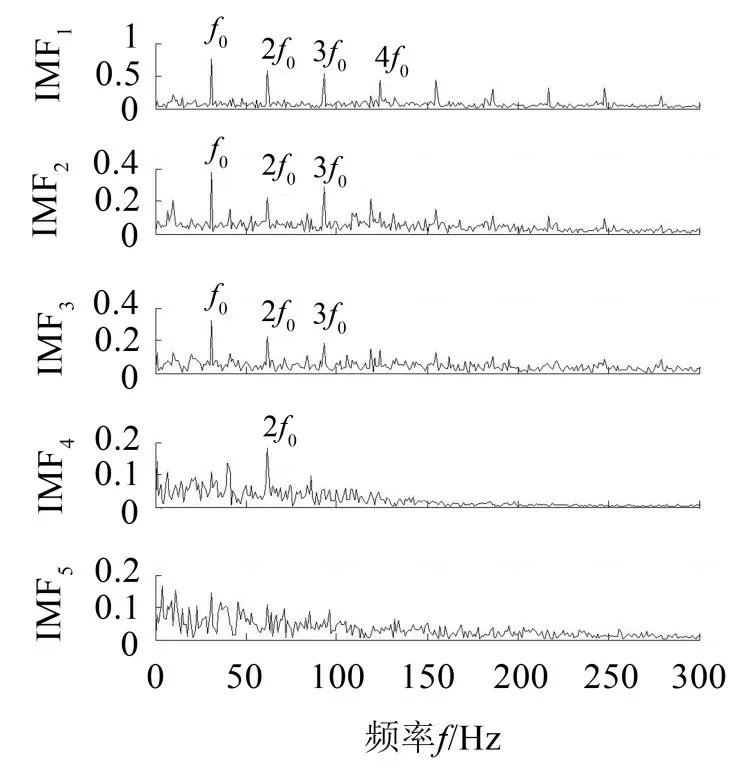
图12 EMD分量的包络谱

图13 ASTFA分量的包络谱

图14 CDOOD分量的包络谱

由图12可以看出，IMF1至IMF4分量解调后均可在fo及其倍频处得到较为明显的谱线，符合轴承的故障特征频率。由图13可以看出，IMF1分量解调后可在fr处得到较为明显的谱线，但在其余非特征频率处也存在幅值更高的噪声谱线，影响对齿轮故障的判断。IMF2分量解调后可在fo及其倍频处得到较为明显的谱线，符合轴承的故障特征频率。由图14可以看出，INBC1分量经过包络解调后，在频率fo及其倍频处谱线清晰可见，这与轴承故障特征相吻合。在INBC2分量的包络谱中存在一条很明显的谱线，且频率正好是齿轮的啮合频率，分量的包络谱在fo处也存在明显的谱线。

对比图12至图14可知，各分量解调以后，EMD可提取轴承的故障信息，ASTFA 和CDOOD 可同时提取轴承和齿轮的故障信息，与ASTFA 相比，CDOOD在提取齿轮故障信息时，其幅值更大，受噪声影响更小，效果更明显。综上所述，此方法具有能够分别提取轴承以及齿轮故障特征的优点，因此，CDOOD 方法能够有效应用于旋转机械复合故障诊断。

由此可以说明该方法既可以把复合故障信号中的轴承故障特征提取出来，也可以将低频的齿轮故障特征提取出来，这就为CDOOD 方法能够应用于旋转机械复合故障诊断提供了有效证据。

4 结 语

提出了一种新的适合处理非线性与非平稳信号的信号分解方法——CDOOD 方法，相对ASTFA 和EMD，CDOOD具有以下优点：

（1）CDOOD只需对滤波器参数进行优化，其优化参数的个数远远小于ASTFA的优化参数个数，从而大大减少了计算量。

（2）CDOOD 使用复数微分算子约束单分量满足局部窄带信号的条件，与ASTFA 相比较，克服了包络函数和余弦函数成分有可能发生交叠而导致分量的物理意义不明确的缺点。仿真分析的结果表明，相对ASTFA 和EMD，CDOOD 在端点效应、模态混淆、正交性、准确性等方面具有一定的优越性。