基于ASL-Isomap流形学习的滚动轴承故障诊断方法

王振亚，戚晓利，吴保林

（安徽工业大学 机械工程学院，安徽 马鞍山243032）

滚动轴承作为应用广泛且容易损坏的零部件，其工作状态直接影响到整个机械系统的工作性能，因此对滚动轴承进行故障诊断有着重要的现实意义[1–3]。为全面表征滚动轴承在不同运行状态下的故障特征，通常从单域/多域提取特征[4]，这导致所提取的故障特征集呈现出非线性、高维等特性，不仅加大了分类器的工作负担，也难以得到理想的故障诊断效果，因此，有必要对高维混合域故障特征集进行降维处理，以获取利于识别的敏感低维特征[4–5]。

数据降维方法可分为线性降维方法和非线性降维方法。线性降维方法包括主成分分析算法(Principal component analysis，PCA)、线性判别分析方法等[5–6]，但将线性降维方法应用于非线性滚动轴承故障数据时，往往难以探索出固有数据的内部几何结构。近年来，基于几何思想驱动的流形学习方法能有效挖掘出隐藏在高维数据集中的低维流形，为实现高维、非线性的滚动轴承故障特征数集特征约简和高精度的模式分类提供了更为理想的解决思路[4–7]。经典流形学习算法主要包括等度规映射方法(Isometric mapping, Isomap)、局部线性嵌入方法(Locally linear embedding,LLE)、拉普拉斯特征映射方法(Laplacian Eigenmaps,LE)等[4–7]。

L-Isomap 方法通过引入LMDS 算法降低了Isomap 计算复杂度[8]，但是传统的L-Isomap 方法在很大程度上依赖于构建的局部邻域能否正确反映流形的内在结构。若近邻参数选取过大，容易造成“短路”现象；若近邻参数选取过小，则会出现邻域“不连通”现象[9–11]。文献[10]利用残差寻优来选取全局最优近邻参数，文献[11]利用图算法优化邻域选取，但这些算法比较耗时，并且当数据分布不均或流形存在扭曲时，可能无法有效得到全局最优参设，导致降维效果产生较大偏差。此外，L-Isomap 方法预先需要在流形表面选取稀疏分布的界标点代表流形拓扑结构，通常采用随机方法进行界标点的选取，可能会造成降维效果的不稳定。有学者将聚类算法的SOM[12]应用于界标点位置的选取，取得较好降维效果，但界标点数量作为超参数仍需用户手工设定。

针对L-Isomap 方法存在的邻域构造和界标点选取问题，本文提出一种ASL-Isomap流形学习新方法。一方面利用本征维数和局部切空间评价的方法进行自适应邻域构造，另一方面采用SOINN[13]方法选取界标点。为量化“混合域故障特征集+ASLIsomap”故障特征提取效果，采用学习速度快、泛化能力强的KELM[14]进行诊断识别。圆柱滚子轴承故障诊断实验结果表明所提方法能有效、精准地诊断出滚动轴承各故障类型。

1 ASL-Isomap降维方法

1.1 自适应邻域选取

本文利用本征维数和局部切方向的方法评价每个数据点的流形趋势（即评价数据集的密度和曲率），达到自适应邻域选取的目的，使低维数据更能反映高维数据的本质流形，具体过程包括：

(1) 本征维数估计；

(2) 局部切空间评价。

1.1.1 本征维数估计

本征维数d 估计过大，输出数据不可避免包含冗余信息和噪声；反之，高维空间中不同点在低维空间会发生交叠。最大似然评估(Maximum likelihood estimation，MLE)方法[15]是一种新的本征维数评估技术，它通过建立近邻点对间距离的似然函数来得到本征维数的最大似然估计。MLE 法假设每一个小邻域的数据点均匀分布，并且数据点近似地处于服从泊松分布的增长半径的超球空间中，构建数据点xi的局部本征维数最大似然函数表达式如下

式中：Tj(xi)表示从数据点xi到其第j 个近邻点的欧式距离。

然后通过平均化所有数据点的局部本征维数确定出数据集X的本征维数

1.1.2 局部切空间评价

对于输入数据集X，首先对局部数据点构造协方差矩阵，然后对进行奇异值矩阵分解，将特征值降序排序：λ1≥λ2≥…≥λd≥…≥λk。提取前d 个最大特征值对应的特征向量构成基Zi，记为数据点xi的切方向。为充分体现局部数据点的有效信息，需确保λd足够大且λd+1足够小，以保证Zi能够充分表示原始局部数据点的固有信息。定义λd为数据点xi与其邻域点的期望半径，记为

由式(3)可得

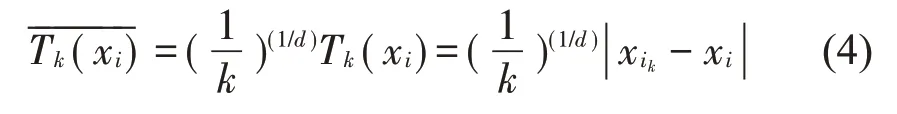
通过迭代增加k值，即在d维超球体中每次加入1 个数据点，直至停止增加数据点。其中的判别根据样本点xi的切方向Zi定义来实现，对应判别表达式如下

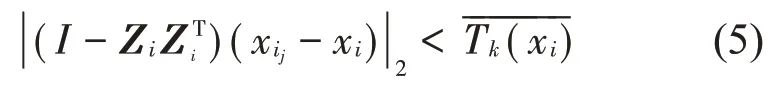
式中：j=1,2,…，k，为不断增加新的样本点，直至式(5)不成立为止。

图1 展示了k 近邻(k-NN)方法和基于本征维度和局部切方向评价方法构建人工数据集上代表点的邻域，其中a点流形曲率较小，b点流形曲率较大。

由图1 可知，基于本征维度和局部切方向评价的方法构建的邻域会随着流形的曲率变化而变化：曲率较大的地方构建的邻域较小；曲率较小的地方构建的邻域相应较大。这表明该方法能够抓住流形在每点处的局部几何性质，自适应地构建邻域。显然这种自适应性是k-NN所不具备的。

图1 基于2种方法构建邻域

1.2 基于SOINN界标点的选取

SOINN 可在没有先验知识的情况下，在线表示输入数据的拓扑结构，因此可将该方法应用于界标点的选取。

对于输入数据集X，基于SOINN 界标点选取方法具体步骤如下：

(1) 初始化：神经元集合A={L1，L2}；神经元Li的激活次数ML1=ML2=0；神经元之间连接关系C为空集；连接阈值

(2) 在A搜寻第一和第二获胜s1和s2

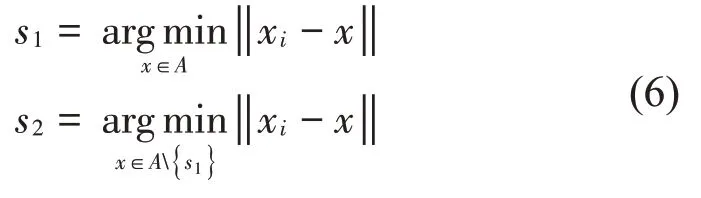
(3) 更新A。若xi满足下式

则xi为新节点，将其并入A中，而后进行下一个神经元的处理。若s1和s2之间不存在连接，则

更新Ms1和age(s1,Li)

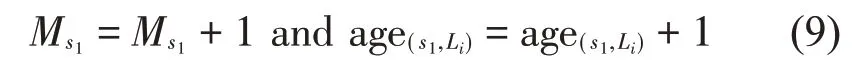
将2 个获胜节点往输入数据方向移动，并删除获胜点中年龄大于agemax的连接，进而更新神经网络GM。

(4) 更新Ts1和Ts2

(5) 删除集合A 中奇异节点，最终得到A={L1,L2,⋅⋅⋅,Ln}。为确保A是输入X的子集，对A进行调整得到L={xl1,xl2,⋅⋅⋅,xln}，其中xli为

1.3 ASL-Isomap方法流程

本文提出一种ASL-Isomap流形学习方法，对于输入维数据集X，具体步骤如下：

(1) 利用SOINN 算法确定合适的界标点集合L={xl1,xl2，…,xln}。

(2) 计算全数据集的欧氏距离矩阵D(N×N)

并采用基于本征维度和局部切方向评价的方法进行自适应邻域图G的构造，若数据点xj是xi的近邻点，则两点之间有边连接，且边长为D(i，j)；否则不连接。

(3) 若界标点xli与样本点xj有边连接，设置其最短路径为dG(xli,xj)=dG(xli,xj)；否则dG(xli,xj)=∞，然后利用Dijkstra算法寻找最短路径，并构造出近似测地距离矩阵DG={dG(xli,xj)}n×N

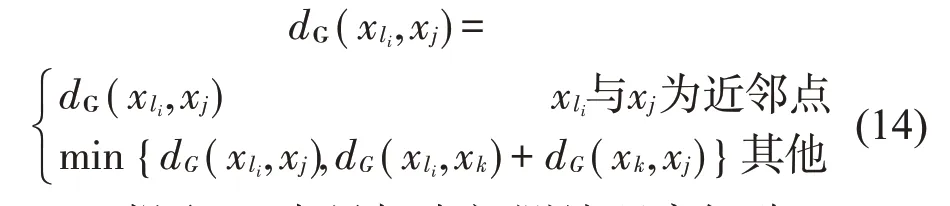
(4) 提取DG中界标点间测地距离矩阵Dn(n×n)，运用MDS算法计算出界标点的映射矩阵M

式中：λi表示第i 个特征值表示λi对应的特征向量。

(5) 抽取DG中界标点与剩余样本点间的测地距离矩阵Dn,N-n(n×N-n)，应用LMDS 计算数据点xi的低维坐标

式中：Δxi为数据点xi与n个基准点的距离向量，Δn为Dn的每个值求平方所得矩阵为Δn的列平均矩阵M #为

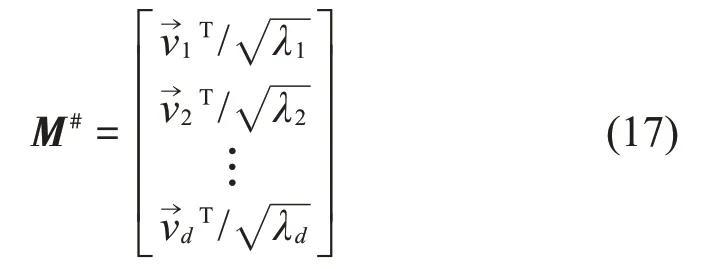
图2为利用ASL-Isomap和L-Isomap将3维空间中的Swiss roll 数据集向2 维空间进行的非线性映射。由图2(c)、图2(e)对比可知：自适应邻域构造避免了k-NN“短路”现象的发生；SOINN界标点选取方法较传统随机选取界标点方法更能表征数据拓扑结构(图2 中▽表示界标点)。由图2(d)、图2(f)数据点颜色分布对比可知：ASL-Isomap 成功地将3 维的Swiss roll 数据集映射至2 维空间，而L-Isomap 映射结果产生严重变形。上述分析验证了ASL-Isomap方法的可行性。

2 基于ASL-Isomap 流形学习的滚动轴承故障诊断方法

基于ASL-Isomap 流形学习的滚动轴承故障诊断实现流程如图3所示，具体步骤如下：

步骤1 在一定转速下以采样频率fs采集每种运行状态样本N组，其中每种状态随机选取z组样本作为训练样本，剩余作为测试样本。

步骤2 对表征不同故障特征的训练样本和测试样本分别提取时域、频域、时频域、复杂域特征参数，合并成高维混合域故障特征集。

步骤3 将训练样本和测试样本的混合域特征集输入至ASL-Isomap方法中进行维数约简，得到d维子空间流形。

步骤4 将训练样本的d 维子空间流形应用于KELM 故障预测模型的构建，再利用训练好的KELM模型对测试样本的d维子空间流形进行模式识别，根据分类器输出结果确定出滚动轴承的故障类型。

图2 Swiss roll数据集上ASL-Isomap与L-Isomap方法对比

图3 故障诊断模型

高维混合域故障特征集可较全面地提取出滚动轴承不同故障特征信息，其包含：11 个时域特征指标、13 个频域特征指标(时域、频域特征指标构造参见文献[16])；对原始信号进行变分模态分解(VMD)[1]，得到K 个本征模态分量，从时频域提取K个本征模态分量的能量信息以及对本征模态分量组成的K维矩阵进行奇异值分解得到K个奇异值共同构成时频域特征指标；计算原始信号在不同尺度下的模糊熵值[17]，构成复杂域特征指标。ASL-Isomap在滚动轴承故障诊断方法中起到了关键性作用，它自动衔接了高维混合域故障特征集和KELM 分类器，能够有效提取出便于识别的敏感、低维的子空间流形，是实现滚动轴承高精度诊断的关键技术。为直观、准确地呈现出滚动轴承诊断结果，还需利用机器学习方法对ASL-Isomap 维数约简得到的特征矢量进行模式识别，核极限学习机(KELM)分类器是针对极限学习机(Extreme learning machine，ELM)[18]的随机映射缺陷，提出的一种改进的新型网络学习方法，与传统分类器相比，KELM分类器具有学习速度快、泛化能力强、鲁棒性好等优势，可以快速、稳定、精确地实现故障类别的量化表征。

3 滚动轴承故障诊断实验

以滚动轴承处于正常状态和发生不同部位故障的诊断实验来验证本文所提方法的有效性。实验测试轴承选用4210 型圆柱滚子轴承，利用SG 双色金属电刻机分别在内圈及滚动体上进行故障加工来模拟真实故障，用来进行实验与数据采集。图4 为滚动轴承故障诊断实验平台，其中电机转速为1 800 r/min，利用加速度传感器分别采集正常滚动轴承和具有内圈故障、滚动体故障以及内圈与滚动体混合故障的滚动轴承振动信号，信号采样频率为5 120 Hz，按时间顺序将2 048个采样值作为一组数据样本，分别提取4 种运行状态数据各30 组，滚动轴承4 种状态振动信号如图5所示。

利用所提方法对4210型圆柱滚子轴承4种运行状态进行故障诊断之前，对该方法中涉及的相关参数设置如下：

(1) 随机选取各类运行状态15 组作为训练样本，剩余15组作为测试样本；

(2) 利用VMD进行时频域特征提取时，模态数K 的准确预估决定了VMD 能否从原始振动信号中精确分解出较高的分量，本文将区间[1,8]的整数值分别赋值给K，并通过绘制出对应的VMD各分量的瞬时频率均值曲线来确定最佳K值。

图4 滚动轴承故障诊断平台

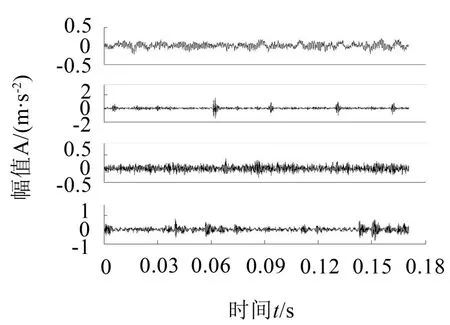
图5 圆柱滚子轴承4种运行状态时域波形

图6展示了圆柱滚子轴承内圈故障样本在K值不同时经VMD分解得到的瞬时频率均值曲线，可以明显看出K 从5 开始出现频率相近分量，因此本文选择K=4作为最佳模态数；

图6 瞬时频率均值曲线

(3) 利用多尺度模糊熵提取复杂域特征时，根据文献[17]，设置嵌入维数m=2，相似容限r=0.15 SD（SD为原始数据的标准差），尺度因子τ=16；

(4) KELM 采用RBF 型核函数，交叉优化惩罚因子和核参数，隐含层激活函数选用sigmoid函数。

按照基于ASL-Isomap 流形学习的滚动轴承故障诊断方法步骤(2)，提取出训练及测试样本信号的11 个时域特征参数、13 个频域特征参数、8 个经VMD分解得到的时频域特征参数以及16个经多尺度模糊熵分析得到的复杂域特征参数，共同构成48维混合域特征向量。通过上述特征参数的组合来全面地提取出能反应滚动轴承不同故障的特征信息。

为验证混合域故障特征提取的优越性，将48维混合域特征集的故障诊断精度同11维时域特征集、13维频域特征集、8维时频域特征集、16维复杂域特征集等单域方法进行对比，直接利用KELM 分类器进行训练与测试，基于不同特征提取方法的故障诊断精度如表1所示。

据表1 可知，混合域特征集的测试样本平均诊断精度达到了91.7%，比单独采用时域特征集、频域特征集、时频域特征集、复杂域特征集时的诊断精度都要高，这表明混合域特征提取方法相比于单域特征提取方法，更能够全面挖掘出反映滚动轴承不同运行状态的特征信息。但该混合域故障特征集具有非线性、非平稳、高维等特性，且存在大量冗余信息，不仅加大了分类器的工作负担，也难以得到高精度的故障诊断效果，因此，有必要对高维数据进行降维处理，以获取利于识别的敏感低维特征。

本文将ASL-Isomap 方法应用于混合域故障集的降维过程中，为验证该降维方法的可行性，将其与PCA、LE、LTSA、Isomap、L-Isomap 等降维方法进行对比，根据6 种方法降维后得到的样本分布如图7所示。

其中，对比方法涉及参数设置如下：本征维数d采用最大似然估计法所确定，计算出全局本征维数估计值d为2.887 7，因为本征维数为整数值，若取2则可能会丢失部分有用信息，影响降维效果，因此综合考虑设置3 为最终的本征维数估计值；通过多次试验确定出近邻参数k 最优值。由图7 可知：6 种降维方法均能够将正常状态与滚动体故障样本完全分离开，但对于内圈故障和复合故障样本，仅ASLIsomap方法没有出现样本混叠现象。上述分析验证了利用ASL-Isomap进行维数约简的可行性。

表1 不同特征提取方法的故障诊断精度

图7 6种方法降维结果

为量化上述6 种降维方法的降维效果，从故障诊断精度与降维性能两方面进行对比与衡量。将各特征压缩结果分别输入至KELM分类器中进行训练与测试，统计出测试样本故障诊断精度；将各特征压缩结果的类间散度Sb与类内散度Sw的比值作为降维性能指标，比值越大，说明同类样本的低维坐标分布越集中，异类样本越分散，降维性能越好。PCA、LE、LTSA、Isomap、L-Isomap、ASL-Isomap 等6 种降维方法的降维效果如表2所示。

据表2可知：兼有全局几何特性、邻域自适应以及界标点优化选取的ASL-Isomap方法对滚动轴承4种故障状态（包括正常状态）有着最高诊断精度和最大降维性能综合指标，降维效果明显优于其余方法，这验证了ASL-Isomap 方法在维数约简方面的优越性。

为验证ASL-Isomap 方法中自适应邻域构造的优越性，将该方法特征压缩结果与不同k 值下LE、LTSA、Isomap、L-Isomap 特征压缩结果分别输入至KELM 分类器中进行训练与测试，得到5 种方法测试样本的诊断精度随k值变化曲线如图8所示。

由图8 可知，对于LE、LTSA、Isomap、L-Isomap这4 种降维方法，当k 值较小时，由于“不连通”现象的出现，导致无法有效呈现流形原结构，进而影响故障诊断精度；当达到各自最高识别精度时，继续增大k值时，出现“短路”现象，造成了故障诊断精度有所下降。而ASL-Isomap具有最高的故障诊断精度，这表明采用自适应邻域构造方法能够避免传统邻域构造方法中的“不连通”现象和“短路”现象的出现，有效提高算法性能。

图8 测试样本故障诊断精度随近邻参数k变化曲线

为验证维数约简的必要性，将原始混合域特征集直接输入至KELM 分类器中进行训练与测试，测试样本诊断精度如表3 第1 行所示；将ASL-Isomap特征压缩后的结果输入至KELM分类器中进行训练与测试，测试样本诊断精度如表3第2行所示。据表3可知，不同故障类型样本之间的统计相关性造成了其自身特征分布结构的混叠与扭曲，从而导致故障诊断精度的下降。而经ASL-Isomap 维数化简后的辨识精度处于较高水平，表明了ASL-Isomap在维数化简的同时消除了不同故障信号之间的相关性，提高了4种运行状态区分度。

为避免应用单一分类器出现的偶然性，利用最小距离分类器、K-NN分类器、极限学习机(ELM)、核极限学习机(KELM)分类器对“混合域故障特征集+L-Isomap”和“混合域故障特征集+ASL-Isomap”特征提取方法进行效果评估，得到的测试样本诊断精度如表4所示。

据表4可知，相比于其他分类器，KELM对两种特征提取方法均具有最高识别精度，表明KELM 在滚动轴承故障模式识别方面具有一定优势。

以上轴承故障诊断试验验证了混合域故障特征集用于故障信息全面挖掘的有效性、ASL-Isomap用于自动维数约减的必要性、KELM 用于模式识别的优越性，即验证了滚动轴承故障诊断方法“混合域特征集+ASL-Isomap+KELM”的自动化、高精度和有效性。

表2 不同降维方法降维效果

表3 KELM分类器对原始混合域特征集和ASL-Isomap特征压缩后特征集的测试样本诊断精度/(%)

表4 不同分类器下测试样本诊断精度/(%)

4 结语

(1)混合域特征提取方法可全面表征各故障类型的特征信息。

(2)所提出的ASL-Isomap方法在维数约简过程中利用自适应邻域构造方法和SOINN 界标点选取方法，使低维数据更能反映高维数据的本质流形，验证实验结果表明该方法在降维效果方面优于现有降维方法。

(3)对圆柱滚子轴承的故障诊断分析表明，本文所提基于ASL-Isomap 流形学习的故障诊断方法集成了混合域在特征提取、ASL-Isomap在维数约简和KELM在模式识别上的优势，能有效、精准地诊断出滚动轴承各故障类型。

尽管如此，本文也存在不足之处，如ASLIsomap 方法仍属于无监督降维方法，降维过程中没有考虑样本标签信息，所以下一步工作将在这方面进行深入研究。