各有一个线性项的两个新的混沌系统及其异结构同步
鲜永菊, 夏 诚, 钟 德, 徐昌彪
(1. 重庆邮电大学 通信与信息工程学院, 重庆 400065; 2. 重庆邮电大学 光电工程学院, 重庆 400065)
混沌理论的研究和应用在许多领域[1-5]得到了极大的关注。自Lorenz于1963年发现第一个混沌吸引子[6]以来,许多学者提出了各种新型混沌系统,如Chen系统[7],Lü系统[8],Liu系统[9]等。大多数混沌系统属于非线性系统,且具有非零特征根的不稳定平衡点,但仍有许多特殊的系统存在。文献[10]报告了一个没有平衡点的系统。Yang等发现了一个只有两个稳定节点的类Lorenz混沌系统[11],同时还发现了一个具有一个鞍点和两个稳定焦节点的混沌系统[12]。孙常春等[13]提出了一个具有无穷平衡点的三维混沌系统。这些系统的发现促进了人们对混沌现象更深入的认识,进一步丰富和完善了混沌理论。
在混沌理论的研究中,另一个重要的研究课题是混沌同步。在实际同步中,由于各种原因很难保证两个系统能完全相同,尤其是混沌同步技术在保密通信中的应用。因为通信系统的发送端和接收端不同,而采用不同的混沌系统将会提高通信系统的安全性。因此,如何设计异结构同步控制器,使得系统能够实现稳定的同步,并将异结构同步控制技术应用到保密通信中增加保密安全性,将更加具有现实意义。罗小华等[14]采用异结构自适应同步控制实现了Liu系统和Rǒssler系统的异结构同步,两个系统分别属于广义Lorenz系统族和广义Chen系统族。李建平等[15]构造主动控制器实现了Lorenz混沌系统和Qi混沌系统的异结构同步,两个系统均属于广义Lorenz系统。于娜等[16]利用Lyapunov直接法在响应系统中构造非线性函数,实现了Lorenz系统和Chen系统的异结构同步。本文采用主动控制同步法对两个新系统实现异结构同步,两个系统均属于广义Lü系统族。
基于以上研究,本文构建了两个只有一个线性项的新型混沌系统,它们均有线平衡,且都为不稳定平衡点。此外,该组混沌系统中的拓扑马蹄和拓扑熵也通过拓扑马蹄理论和数值计算进行了讨论。基于条件Lyapunov稳定性理论,采用主动控制同步法实现了两个新混沌系统的异结构同步。数值仿真和理论分析验证了所设计控制器的有效性。
1 系统模型及其基本特性
系统(1)的数学模型为:
(1)
系统(2)的数学模型为:
(2)
式中:x,y,z为系统变量;ax和az为实常数。
1.1 系统(1)的特性分析
取参数az=-0.3,初始值为[2,2,2] ,系统(1)存在一个典型的吸引子,如图1所示。此时三个Lyapunov指数为L1=0.148,L2=0.001,L3=-2.168,其Lyapunov维数为DL=2.070,显然系统(1)处于混沌态。
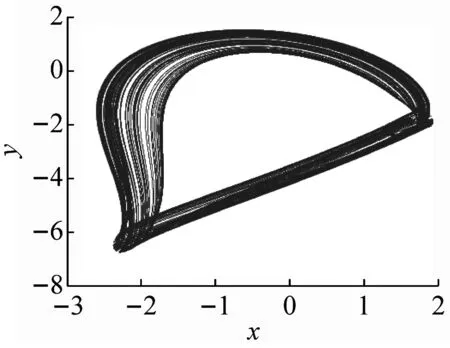
(a) x-y

(b) x-z

(c) y-z图1 系统(1)的相图Fig.1 Phase diagram of system (1)
1) 平衡点及稳定性
令式(1)的左边等于0,得:
(3)
取az=-0.3时,系统(1)的平衡点为:
S0=(0,y*,0)(y*∈R),
S1= (0.381,-0.155,0.184),
S2= (-0.381,0.225,-0.184)。
其中S0=(0,y*,0)(y*∈R)为线平衡。
线性化系统(1),得其Jacobi矩阵为:
在S0处,特征根为λ1=λ2=0,λ3=-0.3,则S0不稳定;在S1处,特征根为λ1=-0.474,λ2=0.105,λ3=0.437,则S1为不稳定的鞍点;在S2处,特征根为λ1=-0.165+0.192i,λ2=-0.165-0.192i,λ3=-0.338,则S2为稳定平衡点。
2) Lyapunov指数和分岔图
采用Jacobi矩阵方法得Lyapunov指数谱,如图2所示。系统变量z随系统参数az变化的分岔图,如图3所示。可知系统通向混沌的道路为倍周期分岔道路。

图2 系统(1)的Lyapunov指数谱Fig.2 Lyapunov exponent spectrum of system (1)

图3 系统(1)的分岔图Fig.3 Bifurcation diagram of system (1)
1.2 系统(2)的特性分析
取参数ax=-2,初始值为[2,2,2] ,系统(2)存在一个典型的吸引子,如图4所示。此时三个Lyapunov指数为L1=0.632,L2=-0.001,L3=-24.733,其Lyapunov维数为DL=2.026,显然系统(2)处于混沌态。

(a) x-y
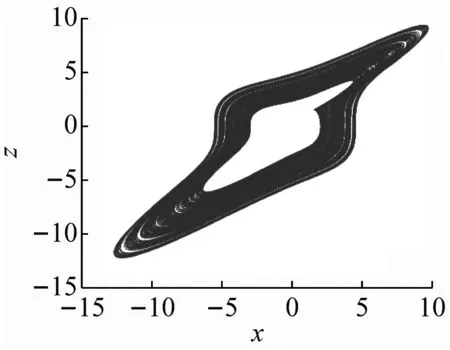
(b) x-z

(c) y-z图4 系统(2)的相图Fig.4 Phase diagram of system (2)
1) 平衡点及稳定性
令式(2)的左边等于0,得:
(4)
取ax=-2时,系统(2)的平衡点为:
S0=(0,y*,0)(y*∈R),
S1=(2.219,0.901,2.219)。
其中S0=(0,y*,0)(y*∈R)为线平衡。
线性化系统(2),得其Jacobi矩阵为:
在S0处,特征根为λ1=λ2=λ3=0;在S1处,特征根为λ1=3.634+4.478i,λ2=3.634-4.478i,λ3=-15.381。可知平衡点都是不稳定点。
2) Lyapunov指数和分岔图
采用Jacobi矩阵方法得Lyapunov指数谱,如图5所示。系统变量z随系统参数ax变化的分岔图,如图6所示。可知分岔图呈倒分岔,即系统通向混沌的道路为倍周期分岔道路。
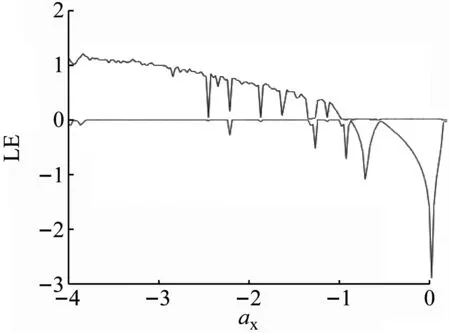
图5 系统(2)的Lyapunov指数谱Fig.5 Lyapunov exponent spectrum of system (2)
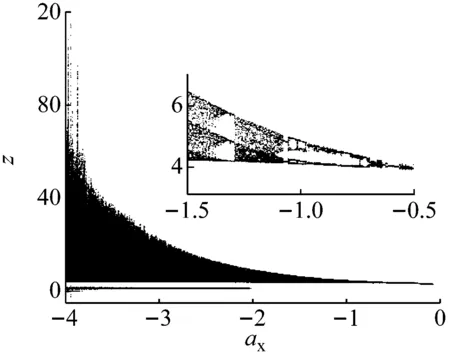
图6 系统(2)的分岔图Fig.6 Bifurcation diagram of system (2)
2 新系统中的拓扑马蹄与拓扑熵
令Z为度量空间,D是Z紧子集,H:D→Z是一个满足存在D的m个互不相交的连通子集[D1,D2,…,Dm],且对于每个Di都有H|Di连续。





推论1[17-19]如果Hm(D1)|→D1,Hm(D1)|→D2,Hn(D2)|→D1且Hn(D2)|→D2,那么存在一个紧不变子集K⊂D,使Hm+n|K半共轭于2位移映射,并且拓扑熵为ent(H)≥1/(m+n)log 2。
例1系统(1)的拓扑马蹄与拓扑熵
取az=-0.3,初始条件为[2,2,2]。选取的Poincare截面为:
Π={(x,y,z)|z=0}
定义Poincare映射P:Π→Π为:对每个(x,y,0)∈Π,P(x,y,0)是系统(1)在初始条件(x,y,0)的流下的第一回归映射。经过多次尝试,找到了一个拓扑马蹄,如图7所示,其马蹄映射,如图8所示。

图7 系统(1)的拓扑马蹄Fig.7 Topological horseshoe of system (1)

图8 系统(1)的马蹄映射Fig.8 Horseshoe map of system (1)
其中D1的四个顶点坐标为:
(1.695957249,-1.852777778)
(1.683596654,-1.906481481)
(1.744749071,-2.015740741)
(1.755157993,-1.952777778)
D2的四个顶点坐标为:
(1.760362454,-1.960185185)
(1.751905204,-2.021296296)
(1.863150558,-2.086111111)
(1.864451673,-2.025000000)
数值计算表明,H下的两个子集D1和D2连续。由图7和图8可以看出:H4(D1)|→D1,H4(D1)|→D2,H2(D2)|→D1,H2(D2)|→D2。根据推论1可知,系统的一次回归Poincare映射与一个2移位映射拓扑半共轭,其拓扑熵为ent(H)≥1/6log 2。因为拓扑熵为正,表明系统(1)是混沌的。
例2系统(2)的拓扑马蹄与拓扑熵
取ax=-2,初始条件为[2,2,2]。选取的Poincare截面为:
Π={(x,y,z)|z=0}
定义Poincare映射P:Π→Π为:对每个(x,y,0)∈Π,P(x,y,0)是系统(2)在初始条件(x,y,0)的流下的第一回归映射。经过多次尝试,找到了一个拓扑马蹄,如图9所示,其马蹄映射如图10所示。

图9 系统(2)的拓扑马蹄Fig.9 Topological horseshoe of system (2)

图10 系统(2)的马蹄映射Fig.10 Horseshoe map of system (2)
其中D1的四个顶点坐标为:
(2.325840232,0.893711420)
(2.350715510,0.811921296)
(2.249348751,0.652970679)
(2.220742182,0.733217593)
D2的四个顶点坐标为:
(2.209548306,0.714699074)
(2.235045466,0.628279321)
(2.155444576,0.509452160)
(2.128703653,0.595871914)
数值计算表明,H下的两个子集D1和D2连续。由图9和图10可以看出:H2(D1)|→D1,H2(D1)|→D2,H2(D2)|→D1,H2(D2)|→D2。根据推论1可知,系统的一次回归Poincare映射与一个2移位映射拓扑半共轭,其拓扑熵为ent(H)≥1/4log 2。因为拓扑熵为正,表明系统(2)是混沌的。
3 混沌系统的异结构同步
采用条件Lyapunov控制方法使系统(1)和系统(2)达到混沌同步。取驱动系统为:
(5)
其中x1,x2,x3为系统变量。
响应系统为:
(6)
其中y1,y2,y3为系统变量,u1,u2,u3为控制器。
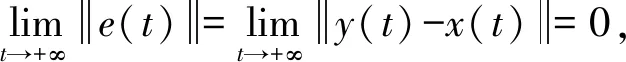
设计控制器为:
(7)
其中k为正的增益常数。
系统的同步误差为:
(8)
采用四阶Runge-Kutta(ODE45)算法进行数值仿真。令驱动系统的初值为x1(0)=2,x2(0)=2,x3(0)=2;响应系统的初值为y1(0)=1,y2(0)=2,y3(0)=3。
同步误差系统的Lyapunov指数谱如图11所示。当k∈[0,0.35)时,同步误差系统的LE1>0,误差系统表现为非稳定状态;当k∈[0.35,5]时,同步误差系统表现为稳定不动点。k=0.35时,其条件Lyapunov指数分别为L1=-0.040,L2=-1.839,L3=-12.470,同步误差e1,e2,e3的曲线如图12所示,显然驱动系统和响应系统达到了稳定同步。即当k≥0.35时,系统的同步误差稳定到原点,即驱动系统和响应系统实现了混沌同步。
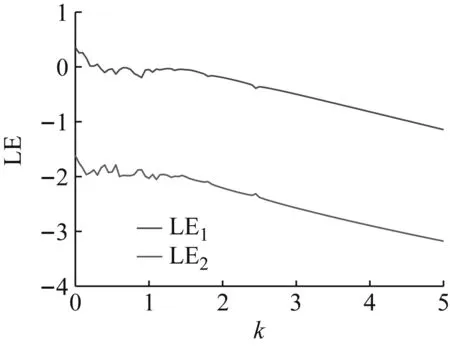
图11 同步误差系统的Lyapunov指数谱Fig.11 Lyapunov exponent spectrum of the synchronization error system

图12 同步误差e1,e2,e3Fig.12 Synchronization errors of e1,e2 and e3
4 结 论
本文提出了两个均有线平衡和各有一个线性项的混沌系统,对该系统的数学性质进行了研究,给出了系统的相图、Lyapunov指数谱和分岔图。借助拓扑马蹄和数值计算,得到了两个系统的拓扑马蹄,其拓扑熵分别为ent(f)≥1/6log 2和ent(f)≥1/4log 2。基于条件Lyapunov稳定性理论,采用主动控制同步法,设计了一个简单的同步控制器,以实现两个系统的异结构同步。理论分析和数值仿真结果表明,所设计控制器是有效的。

