双圆柱体低速并联入水过程空泡及运动特性试验研究

路丽睿， 魏英杰， 王 聪， 宋武超， 刘凯航

(哈尔滨工业大学 航天学院， 哈尔滨 150001)

空投鱼雷、超空泡射弹等跨介质打击型武器在攻击水下目标时，都要经历从空气介质进入水介质的过渡过程，在该运动过程中，运动体经历了入水撞击、空泡形成及演化、全沾湿航行三个阶段。由于气体和液体两种介质在密度、黏度、可压缩性等流体性质上存在差异，使得该过程对运动体水下运动稳定性具有重要意义。

18世纪末Worthington等[1-2]运用当时出现的闪光摄影技术研究了不同球体入水过程产生的物理现象，首次对入水喷溅和入水空泡开展了研究。Malock[3]进一步开展了运动体入水试验，定性分析了球体速度及相对密度对球体入水过程中所产生的空泡的形成和演化、喷溅的影响规律。May等[4-6]针对小型回转体入水运动开展试验研究，获得了运动体入水过程弹道特性和阻力系数。施红辉等[7-9]针对细长体在48～53 m/s速度范围内的入水问题开展试验研究，分析了细长体头型等因素对入水空泡生成和发展变化及自由液面波动特性的影响规律。宋武超等[10]针对回转体倾斜入水开展了相关实验研究，分析了入水速度、入水角度对入水空泡、回转体速度、俯仰及阻力系数的影响规律。方城林等[11]开展了不同头型射弹垂直入水的数值研究，分析了头型对空泡形态演化过程、射弹流体动力及弹道特性的影响规律。杨衡等[12]开展了圆柱体低速入水空泡实验研究，分析了入水速度和入水角度对空泡形态及入水喷溅的影响规律。梅哲力等[13]研究了入水角度对细长圆柱体入水过程中空泡形态及阻力系数的影响规律。路中磊等[14]针对开放空腔壳体入水过程开展了相关研究，并分析了空泡波动与云化的内在机理。孙钊等[15]针对表面润湿性对入水空泡形态的影响开展了数值研究，并分析了半疏水半亲水球体入水后空泡形态非对称特性对运动轨迹的影响规律。

对于并联入水，仅何春涛等[16]开展了圆柱体低速并联入水过程的探索试验，且仅初步分析了空泡演化的非对称现象，并未对其中规律及机理开展深入研究。然而随着水下打击武器及跨介质武器地位的日益凸显，多武器协同打击成为必然发展趋势，深入研究多运动体并联入水流场及弹道特性意义重大。本文基于双圆柱体低速并联入水试验，开展入水空泡特性与运动特性研究，分析入水双空泡演化机理，研究不同入水速度及空泡演化对圆柱体运动特性的影响规律。

1 试验系统与模型参数

本文试验系统由试验水槽、光学测试系统和释放机构三部分组成，如图1所示。试验水槽采用 尺寸为300 mm×300 mm×900 mm 的小型水槽，水槽四壁为钢化玻璃，壁厚 10 mm，槽底垫有缓冲橡胶垫，防止射弹入水对缸体造成破坏。试验光源采用 4 盏 LED 作为背景光，并用柔光屏对背景光进行柔化，使背景光均匀撒布，以达到良好的拍照效果；采用 2 盏 LED 灯作为顶光，以增强空泡内部光照条件，进而增强圆柱体边界清晰度，便于图片数据的后期处理。圆柱体运动过程通过 Photron FASTCAM SA-X 型高速摄像机采集，并通过自编程序对运动轨迹及运动姿态进行提取，以获得圆柱体运动特性。相机采集帧率为 2 000 fps，相机上安装广角镜头，以扩大视野，捕捉更多运动信息。

图1 试验系统示意图Fig.1 Experiment system of water-entry

释放机构由推拉式电磁铁和竖直导轨组成，如图2所示。其中竖直导轨起导向作用，以确保试验模型入水时保持竖直姿态；推拉式电磁铁通过触发开关控制，共用同一个电信号，以确保触发的同步性。当电源接通时，电磁铁推拉杆同时收缩，释放模型。为防止电磁铁收缩引起的支架振动对释放产生影响，导轨和电磁铁分别安装在不同的支架上，导轨支架和电磁铁支架相互独立。

试验模型如图3所示。模型直径D=10 mm，长L=60 mm，模型采用6063铝合金加工，密度为 2.7 g/cm3。

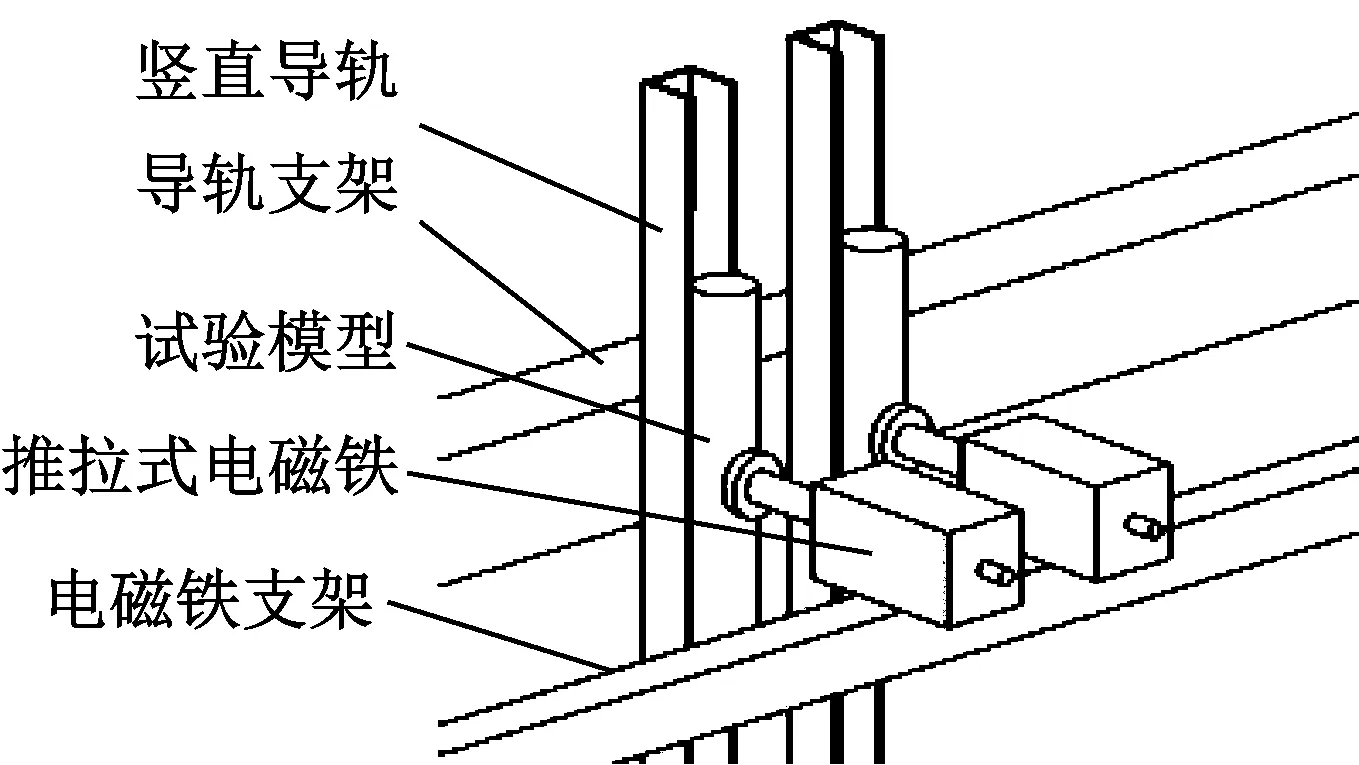
图2 释放机构示意图Fig.2 The mechanism to release the model

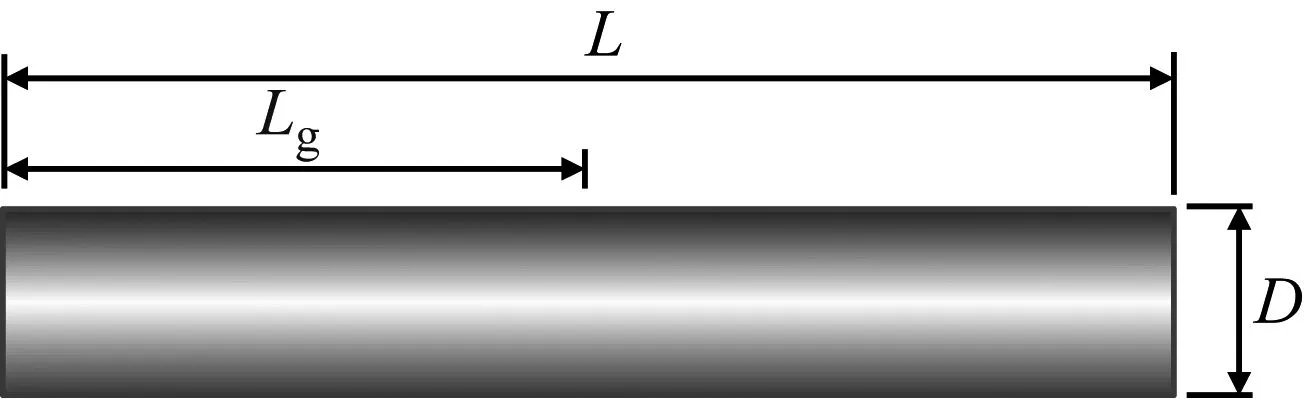
图3 模型尺寸Fig.3 Sketch of water-entry model

2 试验结果分析

2.1 圆柱体并联入水过程空泡形态分析

圆柱体入水过程经历了入水撞击、空泡形成、开空泡、空泡闭合及空泡溃灭五个阶段，具有较强的瞬时性和非定常特性。图4(a)给出了圆柱体单独入水过程入水空泡演化规律。在入水撞击阶段，圆柱体通过冲击作用迅速将动能传递给水面附近流域的流体质点，流体质点获得动能后，向外排开，与圆柱体头部分离，空泡流动形成，如图4(a)中t=0 ms所示；圆柱体在运动过程中通过阻力作用不断将动能传递给前方流域的流体质点，已获得动能的流体质点在惯性作用下继续做向外排开运动，在空泡形态上表现为空泡直径及长度的扩张，此时，空泡演化进入开空泡阶段，如图4(a)中t=12 ms和t=24 ms所示；在开空泡过程中，流体质点受水域压力作用做减速运动，其动能逐渐转换为压力势能，当流体质点运动速度减小至零时，空泡直径达到最大，如图4(a)中t=36 ms所示；此后，流体质点在水域压力和空泡界面张力共同作用下开始向圆柱体中心线反向运动，空泡开始收缩，直至在水面附近或者水下某一深度空泡收缩为一点，此时空泡完成闭合，如图4(a)中t=48 ms到t=60 ms所示；空泡完成闭合后，圆柱体头部仍在诱导流体分离，空泡形成随动，如图4(a)中t=72 ms到t=84 ms所示；流体在随动过程中由于回射流和空泡波动的影响逐渐溃灭，结束了整个空泡周期。

图4(b)给出了轴线径向间距Δd=2Dmm的两个圆柱体并联入水过程中入水空泡演化规律。从图中可以看出，在开空泡阶段，受到来自相邻圆柱体的影响，入水空泡向两圆柱体中间方向的扩张受到了限制，以致两圆柱外侧空泡半径明显大于内侧，空泡形态呈现出明显的不对称特性，如图4(b)中t=0 ms到t=36 ms所示；在空泡闭合阶段，外侧空泡界面率先收缩，在两圆柱体轴线内侧形成了深闭合，闭合点偏离了入水轨迹中心线，如图4(b)中t=48 ms所示；闭合完成后随体运动的空泡在形态上仍旧呈现明显的不对称性，如图4(b)中t=60 ms到t=84 ms所示；由于单空泡的不对称使得圆柱体所受水动力不对称，进而使圆柱体运动稳定性受到影响，引起了圆柱体运动轨迹的偏移与运动姿态的偏斜。从图中还可以发现，双空泡形态在空间上呈现出良好的镜面对称特征。

(a) 单独入水空泡形态

(b) 并联入水空泡形态图4 并联入水与单独入水空泡形态(v=1.5 m/s)Fig.4 The cavity of cylinder water entry alone and two cylinder water entry in paraller

结合图5对空泡形态不对称原因解释如下：在开空泡阶段，外侧空泡自由扩张，而内侧空泡的发展受到了相邻圆柱体的影响。空泡在两圆柱体中间区域扩张时，空泡边界附近流体形成了对流，流体质点间动能传递受到限制而转变成流场势能，致使中间区域喷溅高度增加而空泡半径减小，空泡形态呈现出不对称特性。同时，由于中间区域较少的流体获得了来自两个圆柱体的动能，流动速度较外侧区域大，致使该区域流场压力低于外侧空泡界面附近流场压力，导致在空泡闭合阶段，外侧空泡界面在较大压力作用下率先收缩，且收缩速率大于内侧空泡界面，最终使得闭合点偏向两圆柱体轴线内侧。

2.2 圆柱体并联入水过程运动特性研究

为研究圆柱体并联入水过程中，两圆柱体位移和姿态变化规律，建立如图6所示圆柱体运动时间和空间坐标系。以圆柱体触水时刻为时间零点，入水前取时间t<0，入水后取t>0；以水平面为X轴，竖直方向为Y轴，建立固定坐标系XOY研究圆柱体的移动特性；以两圆柱质心为原点，水平方向为x轴，竖直方向为y轴，建立随体坐标系x1o1y1和x2o2y2研究圆柱体姿态变化规律；以圆柱体轴线与y轴的夹角θ的大小表征圆柱体的偏转角，左偏取负值，如图6(b)中θ1。本文开展了两圆柱体轴线间距Δd=2D，入水速度v=1.5 m/s、1.9 m/s、2.3 m/s、2.7 m/s及3.1 m/s五个同步并联入水工况试验。

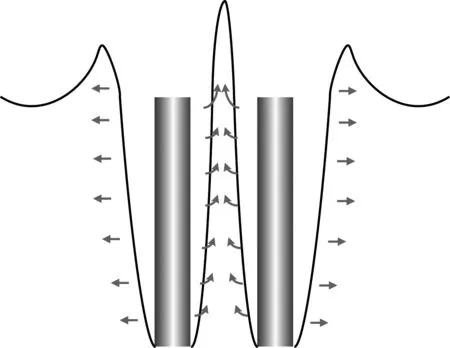
图5 并联入水空泡流动示意图Fig.5 The flow schematic of water entry cavity

(a)(b)

图6 圆柱体运动坐标系

Fig.6 Definition of coordinate system

为分析圆柱体并联入水运动无量纲时历特性，将时间按照下式进行无量纲化：

(1)

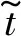
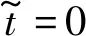
鉴于两圆柱体运动的对称性，后文将基于左圆柱体开展并联入水过程运动特性分析。图8给出了v=1.5 m/s、1.9 m/s、2.3 m/s、2.7 m/s及3.1 m/s工况下圆柱体偏转角对比。从图中可以看出不同入水速度工况下圆柱体姿态偏转运动保持相同趋势，且随着速度的增大，偏转发生时刻逐渐前移。图9给出了空泡闭合时间与圆柱体偏转时间的对比。由上一段的分析可知，圆柱体偏转由空泡非对称闭合引起，因而其与空泡闭合方式及闭合时间关系密切。当v=1.5 m/s、1.9 m/s、2.3 m/s时，空泡闭合方式为深闭合，且闭合时间随着速度增大而变短，因此圆柱体偏转发生时刻逐渐前移，从图中可看出，圆柱体偏转时刻略晚于空泡闭合时刻；当v=2.7 m/s、3.1 m/s时，空泡闭合方式为表面闭合，在该工况下，偏转时刻大幅晚于空泡闭合时刻，说明空泡闭合瞬时的流体作用力对圆柱体姿态影响较小。此时影响偏转运动的主要因素为头部和尾部沾湿航行状态所受流体动力，由于沾湿区域较小，圆柱体转动惯量相对较大，两个速度下流体动力差异对偏转影响不明显，导致两圆柱体偏转时刻较为接近。

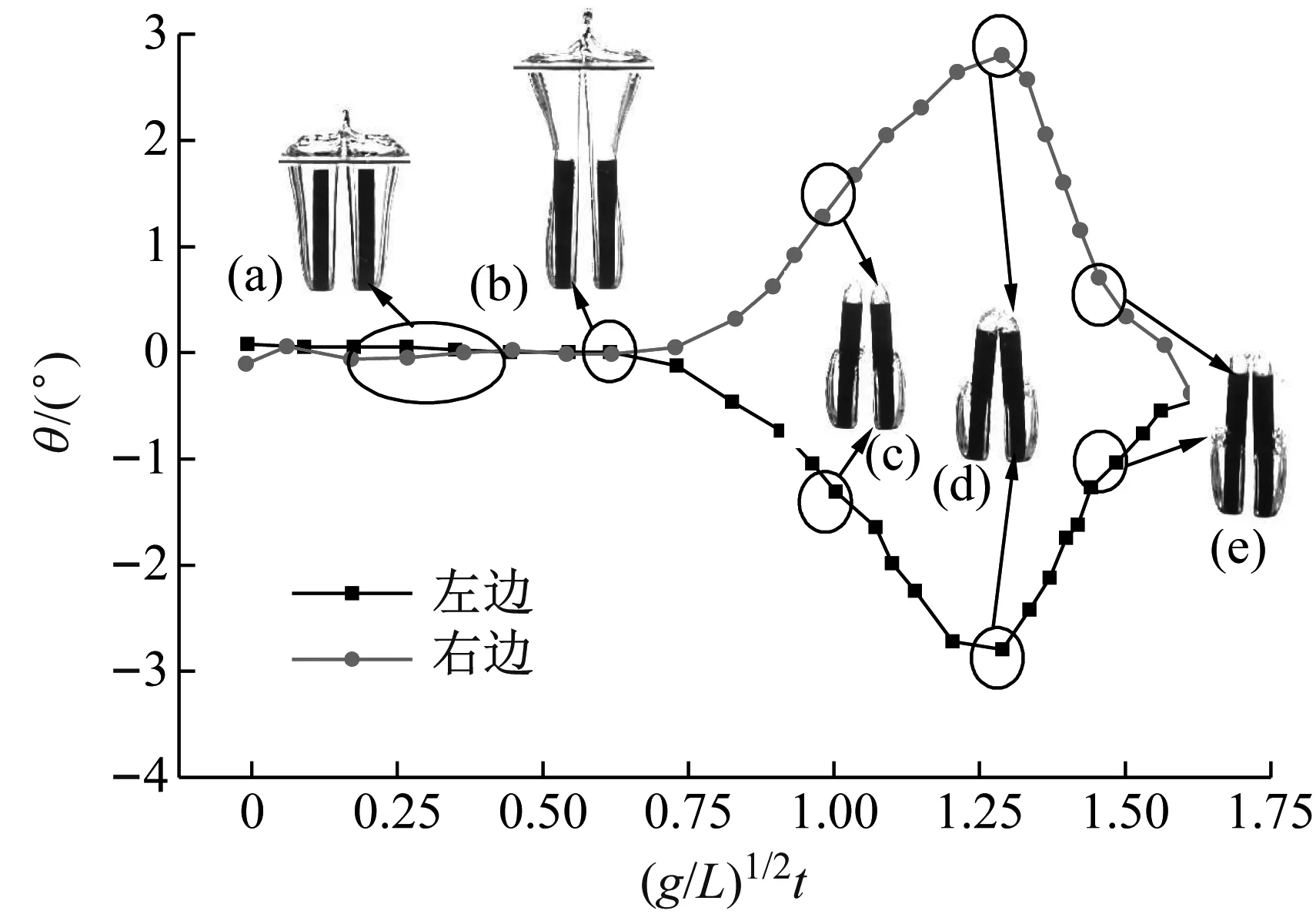
图7 v=1.9 m/s Δd=2D并联入水偏转角随时间变化Fig.7 v=1.9 m/s Δd=2D the variation of rotation angle with times

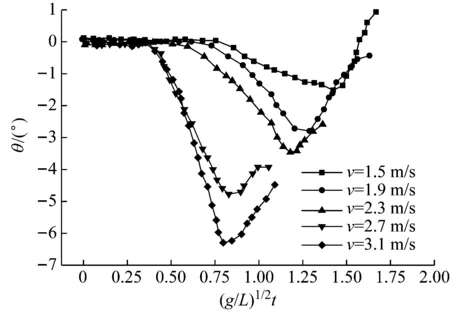
图8 不同速度并联入水偏转角随时间变化对比

Fig.8 Comparison of the variation of rotation angle with different water entry velocities at absolute time coordinate system

为研究并联入水过程中入水速度对位移特性的影响，定义无量纲位移如下：

(2)

(3)

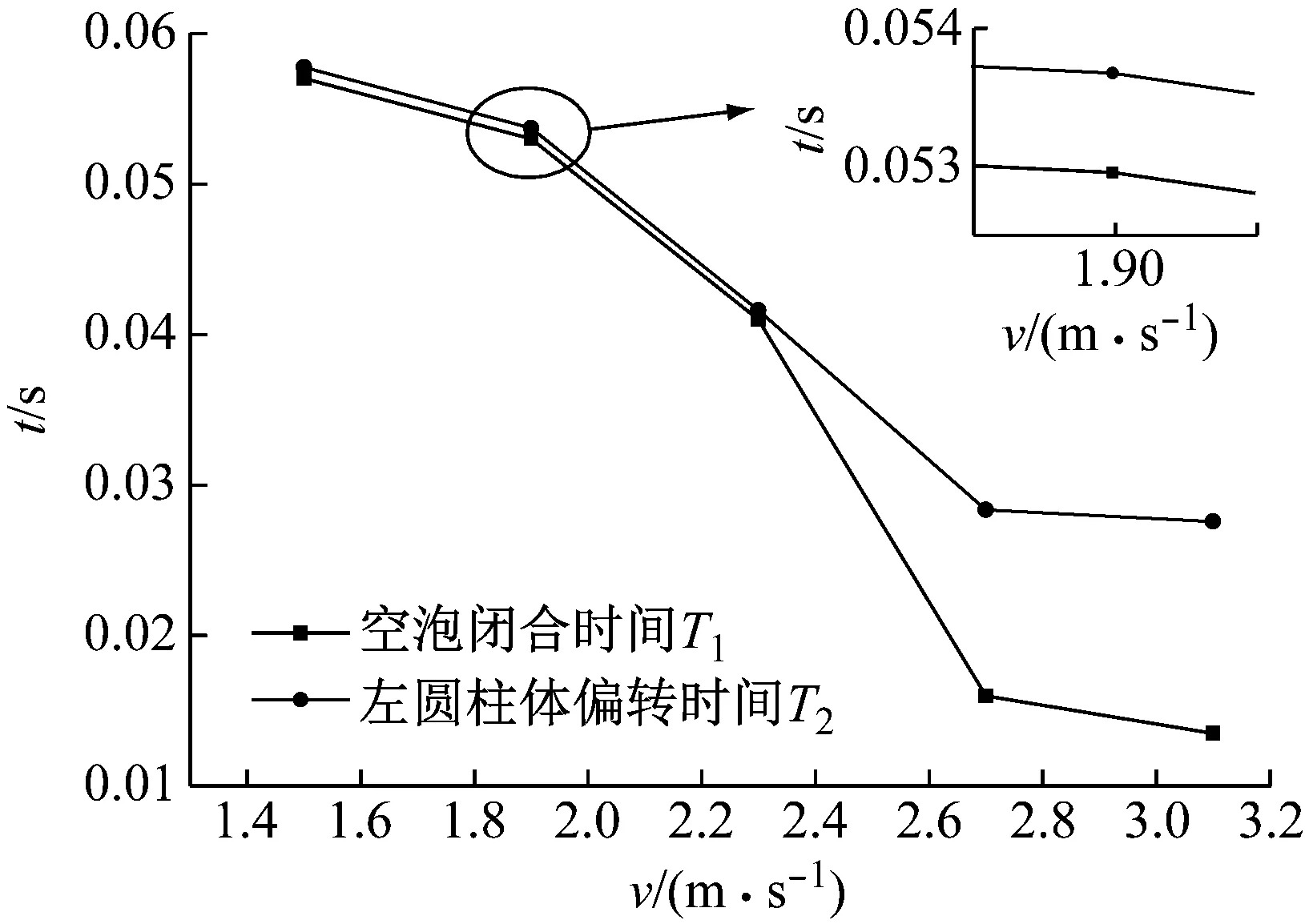
图9 空泡闭合与偏转发生时间随入水速度变化Fig.9 Comparison of time of cavity closure with various water entry velocities

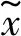
图10 圆柱体质心Y方向无量纲位移变化Fig.10 Variation of Y-displacement with different water entry velocities

图11给出了圆柱体质心在X方向的无量纲位移变化曲线，图12给出了圆柱体头部中心X方向无量纲位移变化曲线。从图11中可以看出，当入水速度较高时，圆柱体质心横向位移呈现先增大后减小的趋势，其原因主要在于，当速度较高时，圆柱体动能大，两圆柱体撞击之后回弹现象显著；当入水速度较低时，在所截取时间范围内圆柱体质心横向位移持续增大，撞击回弹现象不明显。

对图8的分析中指出了影响圆柱体发生偏转的主要因素为非对称流体作用力，结合上一段对图11的分析中所体现的撞击回弹现象可知，影响圆柱体质心横向位移的主要因素为非对称流体作用力和撞击力，其中非对称流体动力的影响又包含间接影响和直接影响两个阶段。从图8和图11可发现，横向位移的产生均发生在偏转时刻附近；对比图11和图12可知，在质心横向位移发生初期，当质心沿着X方向靠拢时，圆柱体头部存在反方向的微幅运动。上述现象表明，在该阶段圆柱体以偏转运动为主，且旋转中心处在质心和圆柱体头部之间的某个位置，质心横向位移由偏转运动直接引起，非对称流体作用力通过影响圆柱体的偏心偏转而间接影响质心横向位移。其原因解释如下：在横向位移发生阶段，圆柱体大部分包裹在空泡内部，圆柱体主要受空泡界面非对称收缩过程中圆柱体轴线左右空泡界面到达圆柱体壁面不同步引起的非对称流体作用力，此时圆柱体头部处于沾湿态且持续诱导空泡流动分离，而柱段却包裹在空泡中，仅受空气流体作用，因此头部水平方向所受到的流体作用力较圆柱体柱段大，导致圆柱体旋转中心偏向质心下方，引起圆柱体偏心偏转，进而引起质心的横向位移。在质心横向位移的后期阶段，从图11和图12可以看出，圆柱体头部中心位移和质心位移方向相同，表明圆柱体在该阶段存在明显的横向运动。其原因在于，两圆柱体并列航行过程中，中间区域流场压力较低，在空泡完成闭合后，圆柱体沾湿面积增加，所受到的非对称流场压力增大，在左右两侧压差的作用下，圆柱体产生横向运动。

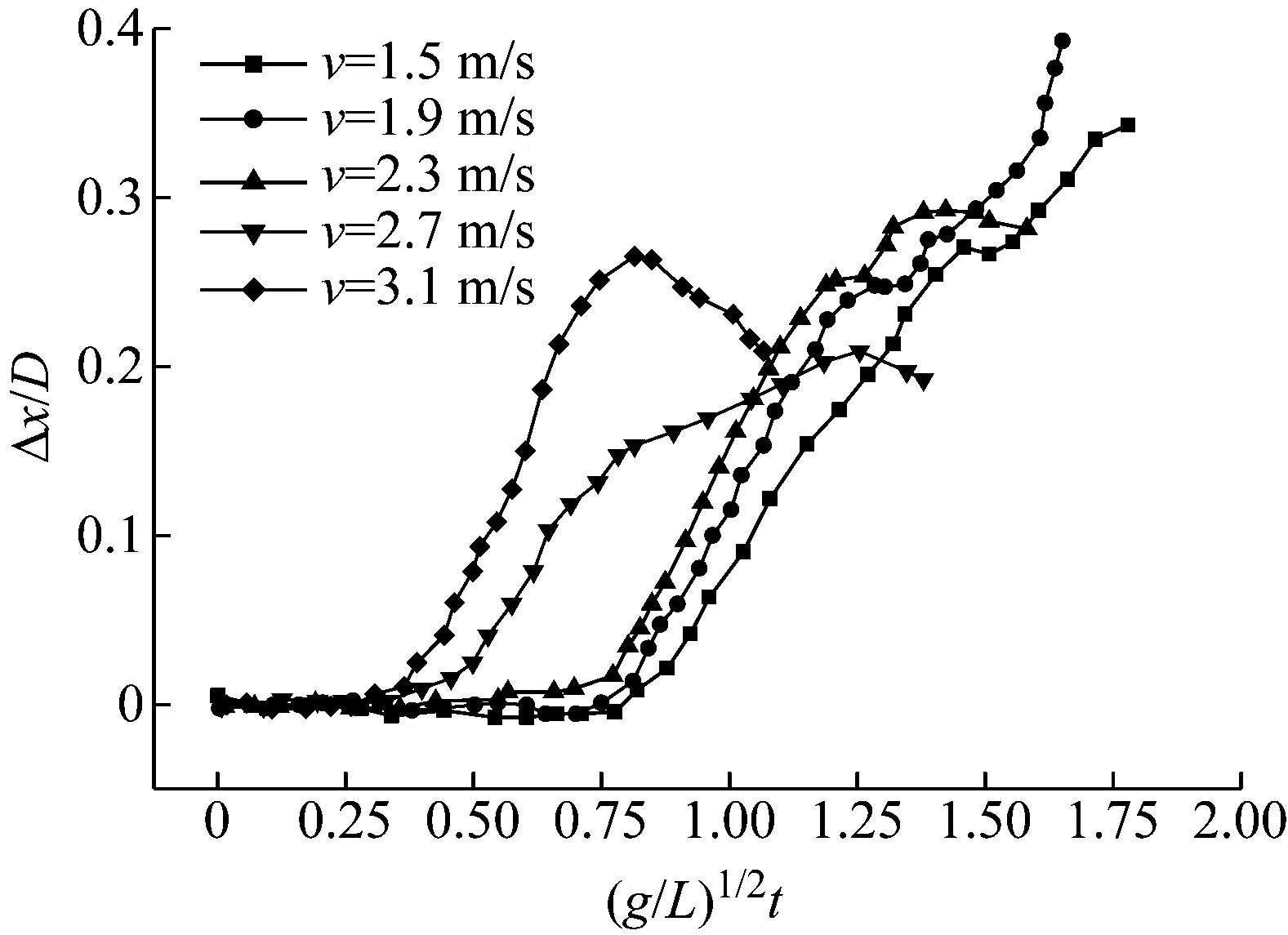
图11 圆柱体质心X方向无量纲位移变化Fig.11 Variation of X-displacement with different water entry velocities

图12 圆柱体头部中心X方向无量纲位移变化Fig.12 Variation of X-displacement of head center with different water entry velocities

在该阶段圆柱体以横移运动为主，非对称流体作用力直接影响圆柱体质心横向位移。

为了进一步说明非对称流体作用力对圆柱体质心横向位移影响的两个不同阶段，图13对左侧圆柱质心横向运动和偏转运动从开始至达到最大值的时历范围进行了提取。从图中可以看出，横向运动和偏转运动发生时刻基本相同，表明质心横向位移由偏转间接引起；当偏转角达到最大后，两圆柱体弹尾相撞，而质心横向位移还在不断增加，表明在该阶段横向位移主要由非对称流体动力直接引起。

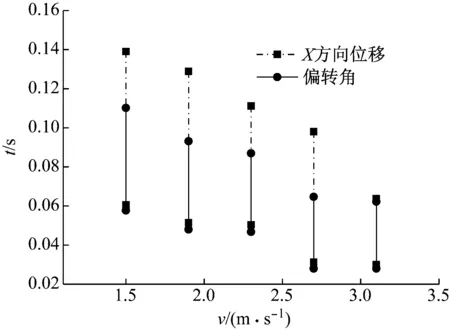
图13 横移与偏转从发生至达到峰值时历范围对比Fig.13 Comparison of the time period from occurring to maximum of X-displacement and rotation

图14给出了横移与偏转达到峰值的时间随速度的变化规律，从图中可以看出，横移与偏转达到峰值的时间随速度的增加而前移。从图中可以发现，当v=3.1 m/s时，横移与偏转达到峰值的时间非常接近，其原因在于：当圆柱体运动速度较高时，圆柱体尾部碰撞回弹现象显著，圆柱体头部依旧持续诱导空泡流动分离，水平方向所受流体作用力较大，导致回弹过程中圆柱体偏转运动依旧为偏心回转，旋转中心位于质心下方，进而导致质心横向位移与偏转角几乎同时开始减小。

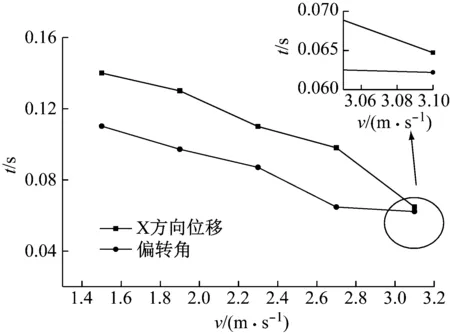
图14 横移与偏转峰值时间随速度变化规律Fig.14 Variation of the time that X-displacement and rotation reach to maximum with times

为进一步分析圆柱体入水过程的运动特性，对圆柱体运动位移变化曲线进行五阶多项式拟合[17]，并对拟合后的曲线求一阶导数，得到圆柱体入水过程中的速度曲线，通过下式对速度进行无量纲化：

(4)

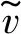
对于姿态角变化，本文截取了圆柱体偏转角增大过程的角位移变化曲线，并对该曲线进行线性拟合，得到其转角变化的平均角速度，如图15所示。从图中可以看出，圆柱体偏转平均角速度随着入水速度增加而增大。其原因在于，圆柱体入水后随着入水速度的增加，Y方向阻力Ry增大，当圆柱体受到扰动发生偏转后，由前文可知，圆柱体旋转中心位于质心g和圆柱体头部中间某个位置m，如图16所示，阻力Ry增大使得围绕旋转中心的力矩加大，进而导致平均角速度增大。从图中还可发现，当入水速度增大至表面闭合阶段后，平均角速度变化率明显加快。该现象间接体现了闭合方式的改变引起了力矩的变化，进入表面闭合阶段后，圆柱体所受力矩较深闭合阶段明显增大。

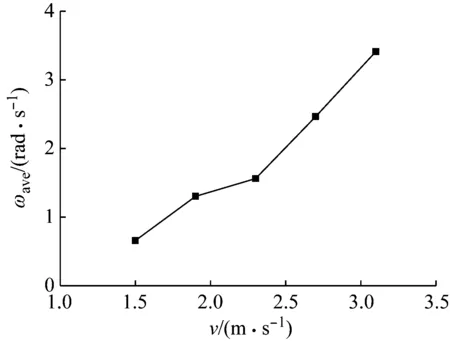
图15 平均角速度随入水速度变化Fig.15 Variation of average angular velocity with water entry velocity

图16 左侧圆柱受力示意图Fig.16 Force schematic of left cylinder

为了分析其内在原因，本文对空泡闭合后的无量纲特征长度进行了提取，特征长度定义为空泡闭合后的长度，如图17中lc所示，并根据式(4)对其进行无量纲化，结果如图18所示。

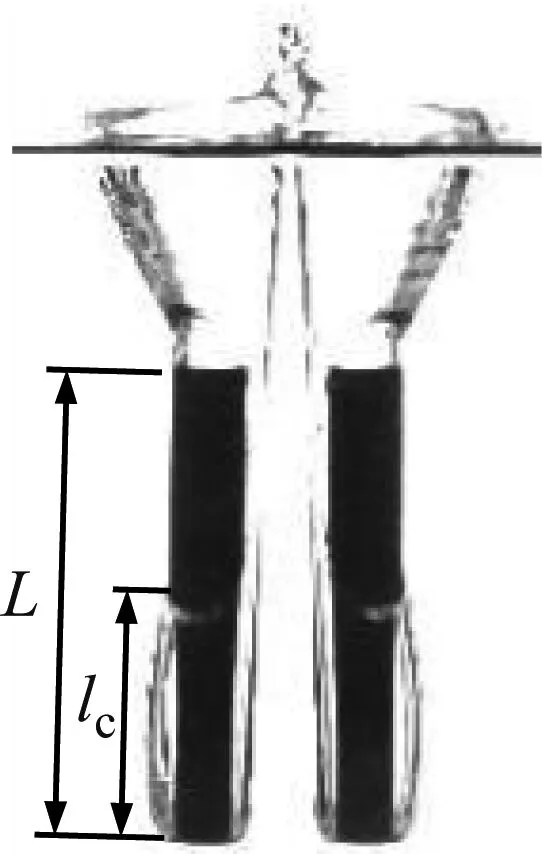
图17 空泡特征长度定义Fig.17 Definition of the cavity length

(5)

从图18可以看出，表面闭合空泡特征长度远大于深闭合空泡特征长度，当空泡形成表面闭合后，圆柱体大部分包裹在空泡内部，弹尾沾湿面积减小，图16中弹尾受到的流体阻力r亦随之减小，使得圆柱体偏转过程所受到的力矩增加。

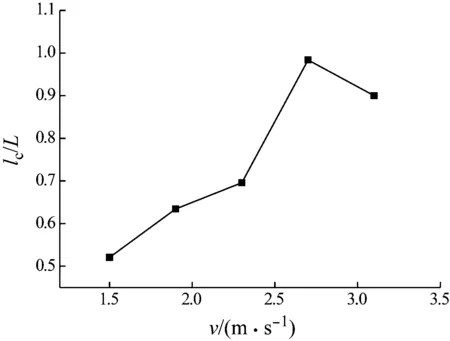
图18 空泡特征长度随入水速度变化Fig.18 Variation of cavity length with the water entry velocitise

图18中圆柱体入水速度大于2.7 m/s后，空泡特征长度由增加变为缩小，其原因解释如下：当圆柱体入水速度大于2.7 m/s后，入水空泡的闭合方式呈表面闭合。表面闭合主要是由于入水撞击在自由液面附近引起的薄膜式喷溅射流在气液界面表面张力作用下收缩回卷，并最终到达圆柱体壁面而形成的闭合。在形成闭合后，与圆柱体壁面接触的流体在黏性作用下随圆柱体向下运动，并在黏性力、气液界面张力作用下带动周围流体一同回卷并向下运动，形成稳定闭合。在并联入水过程中，由于两圆柱体中央区域流场动能向势能转换形成向上的流动，在喷溅射流达到圆柱体壁面完成空泡闭合后，薄膜射流表面张力和内部流体黏性力不足以克服流场向上的惯性作用带动流体回卷并向下运动，此时所形成的闭合不稳定，射流薄膜破裂后会有空气进入空泡，使空泡长度加长。随着入水速度的增加，圆柱体传递给流域的能量增加，使得喷溅射流强度增加，缩短了空泡完成闭合到形成稳定闭合的时间，使得闭合期间进入空泡内的空气量减少，进而使得稳定闭合后空泡的特征长度减小。

图19给出了入水过程Y方向无量纲速度变化曲线。从图中可以看出，当入水速度较低时，圆柱体入水后速度呈现先增大，后减小趋势；当入水速度较高时，圆柱体入水后速度持续减小。其原因解释如下：当速度较低时，在圆柱体入水初期，其所受重力大于阻力，所以圆柱体速度持续增加；随着速度的增加与沾湿面积增大，圆柱体受到的阻力逐渐增大，阻力对速度的贡献占据主导地位，速度开始减小。当速度较高时，入水初期，其所受阻力便大于重力，在图中所截取的运动过程内，阻力始终占据主导地位，圆柱体速度持续减小。

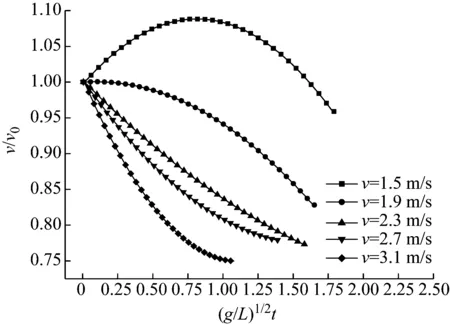
图19 Y方向无量纲速度变化曲线Fig.19 Variation of Y-velocity with the times

3 结 论

本文针对圆柱体低速并联入水过程空泡及运动特性变化规律开展了研究，对比了双圆柱体并联入水与圆柱体单独入水空泡形态差异，量化分析了不同入水速度对圆柱体偏转角、横向位移、纵向位移以及偏转角速度和纵向线速度的影响规律，得到如下结论：

(1) 相比于圆柱体单独入水，并联入水空泡形态呈现明显的不对称性，外侧空泡半径大于内侧，闭合点偏离了圆柱体运动轨迹中心线，在两圆柱体轴线内侧形成闭合；从全局来看，两个空泡形态呈现出良好的镜面对称特征。

(2) 并联入水过程圆柱体偏转运动呈现良好的对称性，偏转发生时刻与空泡闭合方式密切相关；深闭合阶段随着入水速度的增加，偏转发生时刻前移，发生时间与空泡闭合时间接近；表面闭合阶段，随着入水速度增加，偏转发生时刻不再改变。

(3) 入水过程中两圆柱体在竖直方向迁移运动相互干扰较小，横移运动相互影响较大。影响圆柱体横向位移的主要因素为非对称流体作用力和两圆柱体尾部撞击力。

(4) 圆柱体平均偏转角速度随着入水速度增加而增大，在空泡表面闭合阶段，圆柱体所受平均偏转力矩较深闭合阶段大。