角度偏移对微机械陀螺系统响应特性的影响

张利娟， 李欣业， 张华彪

(1. 河北工业大学 机械工程学院， 天津 300130; 2. 天津商业大学 机械工程学院， 天津 300134)

微机械陀螺由于体积小、重量轻、可靠性高等优点，被广泛应用于商业和军事领域。微机械陀螺的性能与其动力学特性紧密相关，因此微机械系统相关动力学问题的研究受到了人们的普遍关注。国内外学者对此进行了比较深入的研究，李欣业等[1-2]分别对简谐激励和参数激励的微机械陀螺系统的动力学特性及其时滞反馈控制进行研究，分析了系统参数和反馈增益及时滞对振幅和分岔特性的影响。尚慧琳等[3]研究了参数激励和具有立方非线性的切向梳齿驱动型微陀螺，利用分岔理论得到了Hopf分岔条件，并通过数值模拟揭示了系统参数对驱动和检测模态振幅和分岔行为的影响机制。文永蓬等[4]通过对微陀螺非线性模型的求解，探讨了驱动微弹性梁和检测微弹性梁的非线性刚度对微陀螺输出的影响规律，研究了微陀螺的带宽在非线性刚度作用下的设计原则。张琪昌等[5-6]分别研究了微机械系统中的空气阻尼与非线性静电力以及驱动器的时滞特性对系统共振频率和响应特性的影响。

对于微机械陀螺而言，除了自身参数外，加工误差的影响也很重要。由于尺寸很小，微机械陀螺的敏感结构通常采用微加工技术一次成型，在现有条件下，其加工误差是很难控制的。加工误差的存在使得微机械陀螺的弹性主轴和驱动/敏感轴不能完全重合[7]，导致驱动模态将部分弹性力耦合到敏感模态，引起了误差信号的出现，直接影响到陀螺仪的性能。Mohammadi等[8]研究了耦合误差对谐波和参数激励的微陀螺系统精度的影响。吝海锋[9]研究了不同误差来源对正交耦合的影响，发现振动结构支撑梁的加工误差是引起结构刚度不对称并产生正交耦合的主要因素，计算了正交耦合系数对梁宽误差和梁倾斜误差的敏感度。 姜劭栋等[10]利用能量方法推导陀螺仪驱动梁的面内刚度，建立陀螺仪的刚度矩阵，推导了交叉耦合系数的理论计算公式。Tatar等[11]利用有限元计算和试验证实正交误差主要来源于机械刚度不对称，并设计了一种闭环控制装置对正交误差进行补偿，该装置可以有效减小正交误差，同时还可以提高系统的机械灵敏度和线性度。贺琨等[12]认为振动结构支撑梁的加工误差是产生模态耦合误差的主要因素，在与该误差对称的位置去除相应材料可以减小甚至消除模态耦合误差，并利用紫外激光对微陀螺样机进行了结构平衡实验。郝淑英等[13]建立的微机械陀螺敏感结构的有限元模型，研究了微陀螺驱动微梁在加工误差下的微梁形状变化对正交耦合误差、模态耦合以及检测信号的影响。Gao等[14]研究了双质量MEMS陀螺仪的最佳正交误差修正方法，比较了电荷校正，正交力校正和耦合刚度校正三种方法，发现耦合刚度校正效果更好。Phani等[15]考虑非对称刚度和阻尼的影响，提出三种基于参数辨识的微机械陀螺系统建模方法，用于确定驱动和敏感模态耦合程度以及两者频率之间的匹配。

虽然很多文献指出加工误差引起刚度不对称是机械耦合误差产生的主要原因，但这些文献更多的关注误差的补偿方法以及加工误差对交叉耦合刚度的影响，针对加工误差对微陀螺系统误差的影响机理的研究并不多见。同时在微机械系统中，非线性是普遍存在的，现有文献大多没有考虑到非线性的影响。

本文的第2部分将考虑微陀螺系统的刚度非线性以及加工误差引起的弹性主轴和驱动/敏感轴之间的角度偏移，建立微机械陀螺的动力学方程，并利用平均法求得了关于系统响应振幅和相位的慢变方程。第3部分基于同伦延拓方法研究了偏移角度对零偏、机械灵敏度和非线性度的影响。

1 微机械陀螺的动力学模型及其周期解

微机械陀螺结构如图1所示，其中微机械陀螺敏感结构的等效质量为m，Ω为被检测的角速度，xa-ya是绝对坐标系，x-y为微陀螺系统的驱动/检测坐标系，x轴为输入轴(驱动模态方向)，y轴为输出轴(检测模态方向)，xp-yp为微陀螺系统弹性主轴坐标系，φ和ψ分别是x和xp以及y和yp之间由于加工误差产生的偏移角度。

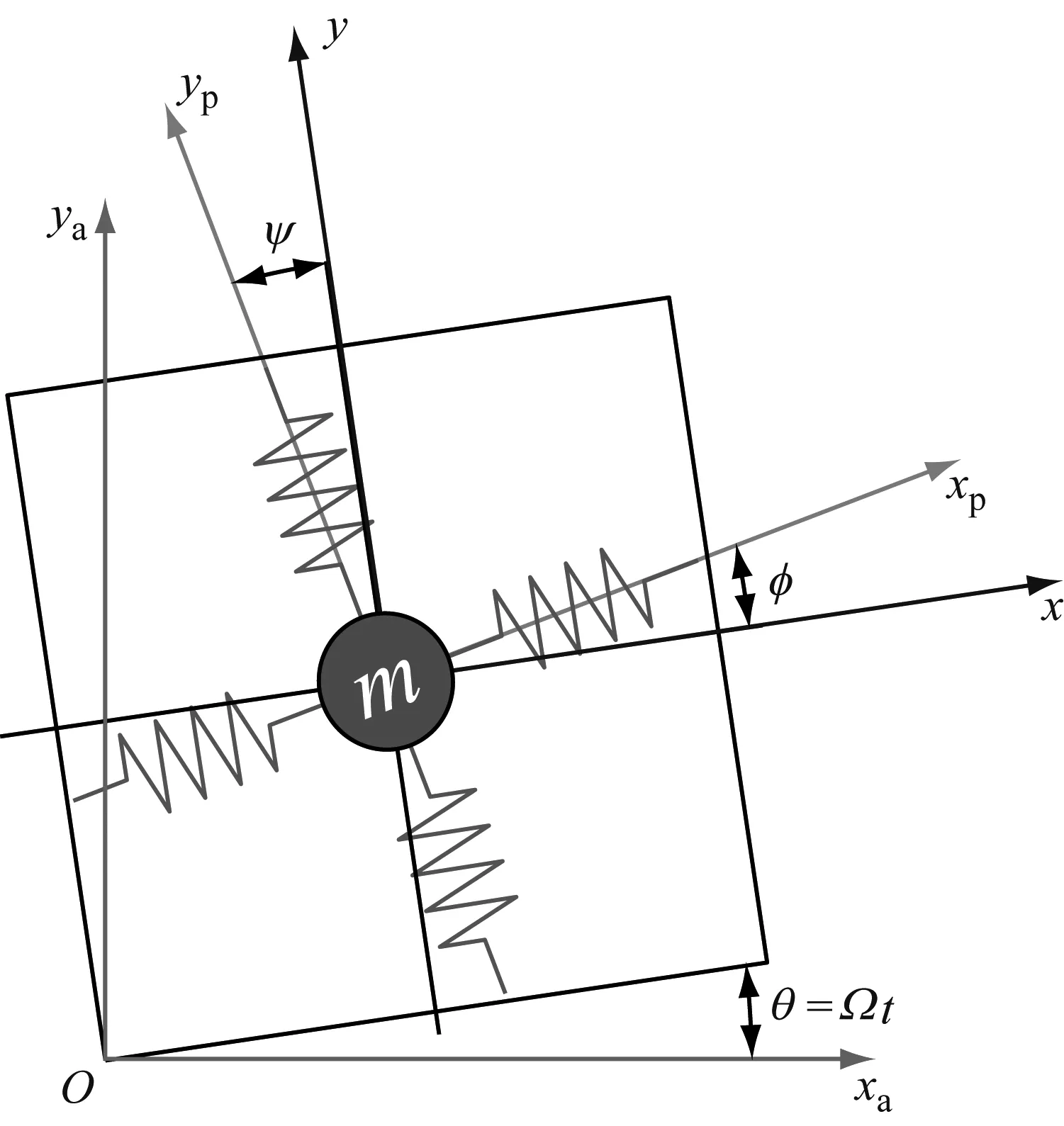
图1 微机械陀螺物理模型Fig.1 The physical model of MEMS gyroscope

容易求得质量块的绝对坐标为

xa=xcosθ-ysinθ,ya=ycosθ+xsinθ

(1)

其中θ=Ωt，xa,ya对t求导可得m的绝对速度为

(2)

因此可得质量块的动能为

(3)

考虑到驱动/检测轴和弹性主轴发生偏斜，弹性主轴的变形量为

(4)

假定微陀螺系统的刚度具有三次非线性，可求得的势能为(此处不考虑微陀螺重力势能)

(5)

式中：kx,ky分别为驱动、检测方向的线性刚度系数，αx,αy分别是驱动、检测方向的非线性刚度系数，Ue为电动势能，有fd=-Fcosωt=-∂Ue/∂x，为x方向电极的驱动力，y方向敏感电极的驱动力是y的近似线性函数，大小为-∂Ue/∂y=key。根据拉格朗日方程，可求得系统的动力学方程为

(6)

式中：cx,cy分别是x,y方向的阻尼系数，考虑到交叉耦合阻尼对系统误差影响很小，这里忽略了交叉耦合阻尼项，G=2mΩ,为陀螺力项系数。方程(6)中出现了线性和非线性的交叉耦合刚度，各刚度项的系数见式(7)。

(7)

定义X=x/r,Y=y/r,τ=ωt，其中r为基准长度。对式(6)进行无量纲化，有

(8)

其中

(9)

X=A1cos(τ+θ1),Y=A2cos(τ+θ2)

可得关于系统振幅和相位的平均方程为

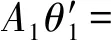
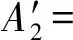
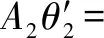
(10)

2 偏移角度对系统响应特性的影响

m=0.01 g,r=1 μm,kx=ky=1.5×103N/m,cx=cy=5×10-3Ns/m,ke=100 N/m，αx=αy=7.5×103N/m3,ω=12 600 rad/s

图2 敏感方向无量纲振幅随被检测角速度Ω变化的 曲线(φ=0)

Fig.2 Variation of non-dimensional amplitude in sensitivity direction with the detected angular velocityΩ(φ=0)

图2和图3中可以看到随偏移角度的增大，系统的零偏也在增大。为了描述偏移角度对零偏的影响，图4给出了偏移角度对零偏的影响，其中A20表示无量纲零偏，可以看到沿-φ=ψ方向，零偏随偏移角度的增大逐渐增大。为了更好的描述偏移角度对零偏的影响，图5给出了几种特殊情况下偏移角度对零偏的影响，可以看到偏移角度为0时，零偏也为0；当只有一个方面有角度偏移时(另一方向角度偏移为0)，ψ和φ对零偏的影响是相同的；当两个方向的偏移角度相等时(φ=ψ)，零偏的值较小；而两个方向的偏移角度互为相反数时(-φ=ψ)，零偏值的变化范围很大，随着偏移角度的增大，零偏迅速增大。图5中同时给出了基于龙格库塔法的数值计算结果，发现其与解析计算结果吻合的非常好。

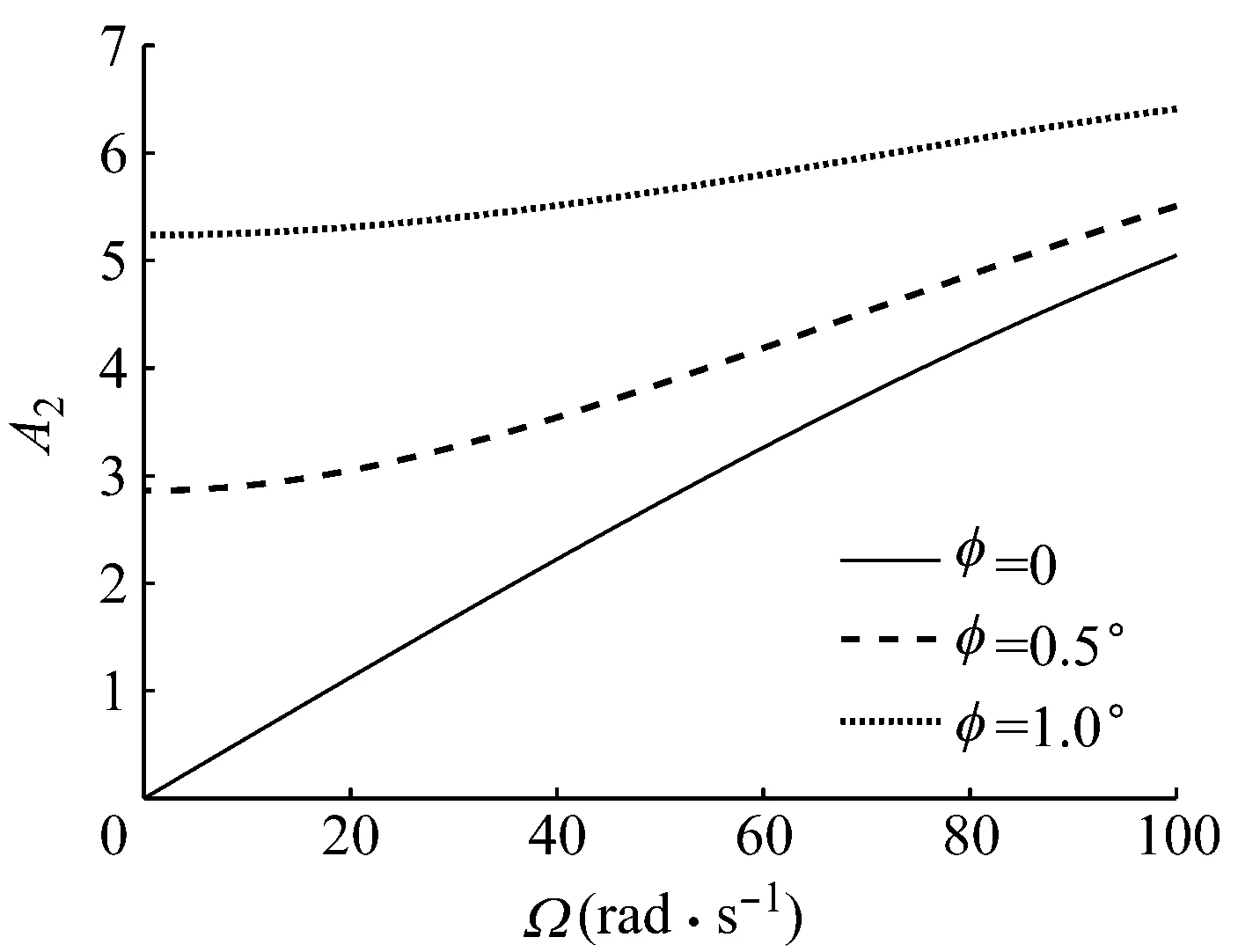
图3 敏感方向无量纲振幅随被检测角速度Ω变化的 曲线(ψ=0)

Fig.3 Variation of non-dimensional amplitud in sensitivity direction e with the detected angular velocityΩ(ψ=0)

图4 偏移角度对无量纲零偏的3D影响图Fig.4 3D influence diagram of deviation angular on the non-dimensional zero bias

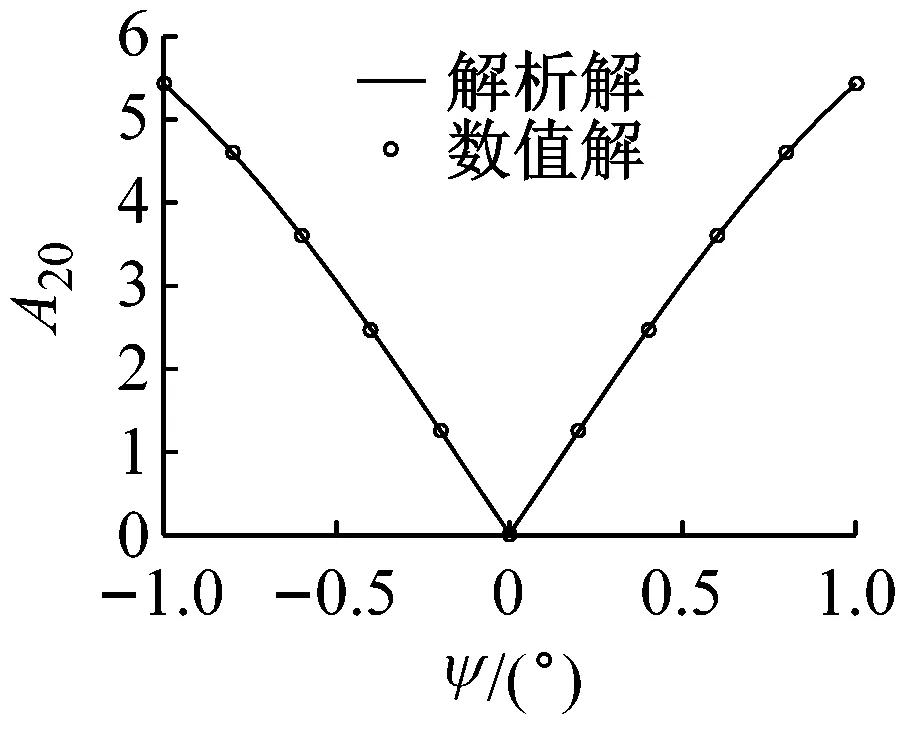
(a) φ=0

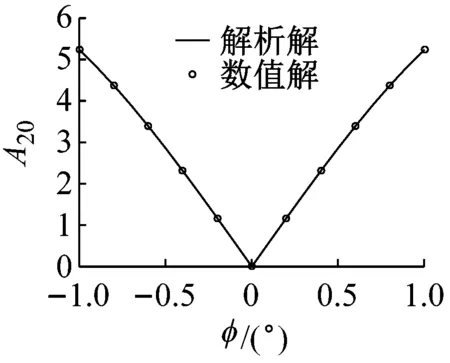
(b) ψ=0

(c) φ=ψ=β

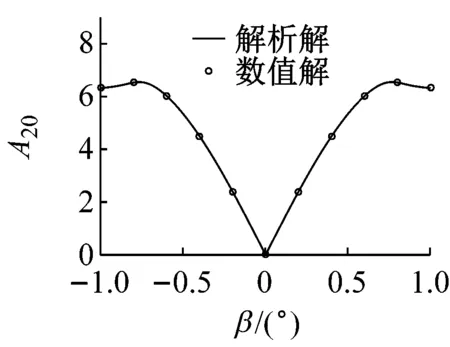
(d) -φ=ψ=β图5 偏移角度对无量纲零偏的影响曲线Fig.5 Influence of angular deviation on the non-dimensional zero bias

此外从图2和图3可以看到，加工误差引起的偏移角度不仅对曲线的零偏有影响，对曲线的斜率和线性程度也有影响，它们在陀螺系统响应特性上分别表现为系统的机械灵敏度和非线性度。为了对系统的机械灵敏度和非线性度进行分析，设定系统的量程为0～50 rad/s，利用最小二乘法对数据进行线性拟合，设定拟合公式为[17]

A2l=SΩ+A20

(11)

式中：S为系统的无量纲机械灵敏度，A20为无量纲零偏。图6给出了敏感方向振幅随被检测角速度变化曲线拟合的结果，其中A2为原始数据，A2l为拟合后的结果，显然两者不可能完全一致，两者之间的差异可以用非线性度来表示，定义非线性度为[17]

(12)

图6 敏感方向振幅随被检测角速度变化曲线的 线性拟合(φ=ψ=-0.5°)

Fig.6 Linear fitting of variation of amplitude in sensitivity direction with the detected angular velocity (φ=ψ=-0.5°)

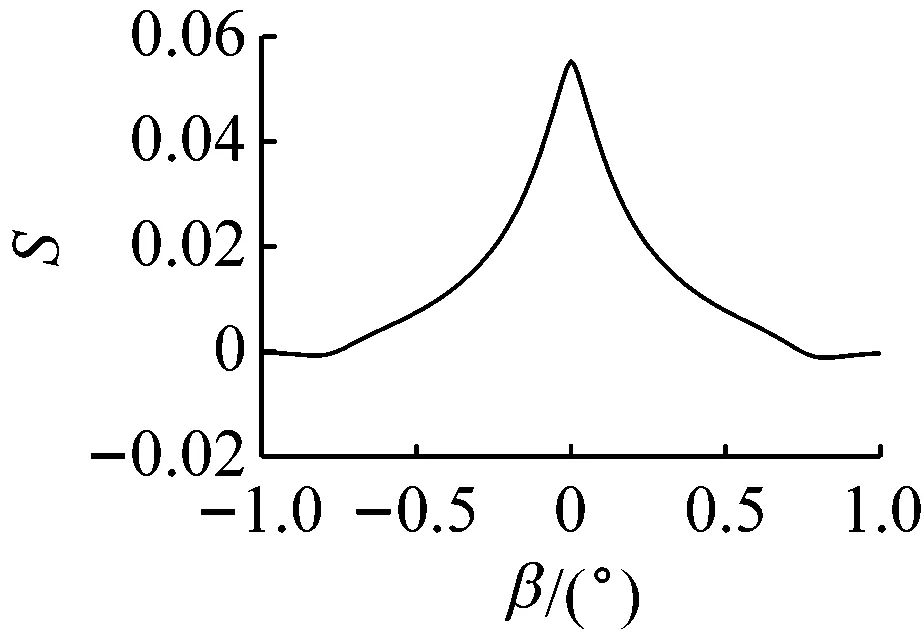
图7和图9分别给出了偏移角度对无量纲机械灵敏度和非线性度的影响，可以看到机械灵敏度沿-φ=ψ方向随偏移角度绝对值的增大而减小，而非线性度的变化相对复杂，沿-φ=ψ方向在偏移角度绝对值较小时，非线性度随偏移角度的增大而增大，在偏移角度较大时，对应局部区域，非线性度出现了一些峰值。为了更好的描述偏移角度对机械灵敏度和非线性度的影响，图8和图10分别给出了几种特殊情况下，偏移角度对无量纲机械灵敏度和非线性度的影响，可以看到偏移角度为0时，无量纲机械灵敏度最大，非线性度最小；当只有一个方面有角度偏移时(另一方向角度偏移为0)，ψ和φ对无量纲机械灵敏度和非线性度的影响是相同的；当两个方向的偏移角度相等时(φ=ψ)，无量纲机械灵敏度和非线性度随偏移角度的变化幅度很小，且机械灵敏度较大，而非线性度较小；而两个方向的偏移角度互为相反数时(-φ=ψ)，机械灵敏度和非线性度随偏移角度变化剧烈，随着偏移角度的增大，机械灵敏度迅速减小，而非线性度迅速增大，且非线性度在某些参数范围出现了峰值。图8和图10中给出了基于龙格库塔法的数值计算结果，发现其与解析计算结果吻合的非常好。

图7 偏移角度对无量纲机械灵敏度的3D影响图Fig.7 3D influence diagram of deviation angular on the non-dimensional mechanical sensitivity

(a) ψ=0

(b) φ=0

(c) φ=ψ=β

(d) -φ=ψ=β

图8 偏移角度对无量纲机械灵敏度的影响

Fig.8 Influence of deviation angular on the non-dimensional mechanical sensitivity

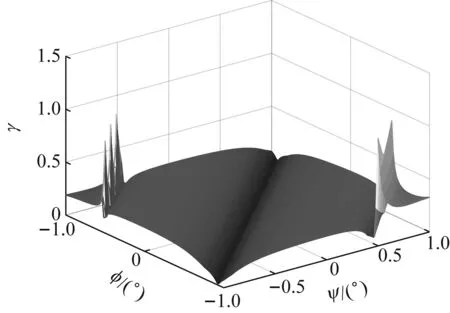
图9 偏移角度对非线性度的3D影响图Fig.9 3D influence diagram of deviation angular on the nonlinearity

对于理想的微陀螺系统，我们希望其零偏和非线性度较小，而机械灵敏度较大，图4、7、9中可以看到当偏移角度ψ和φ满足一定关系时，系统的零偏、非线性度和机械灵敏度取极值。图11给出了系统零偏、非线性度取极小值，机械灵敏度取极大值时ψ和φ的关系曲线，可以看到三条曲线是重合的，当偏移角度接近该曲线时，微陀螺系统的零偏、机械灵敏度和非线性度都较好。在工程中，微机械陀螺的敏感结构加工出现误差时，需要对其进行修型，修型并不需要将每个方向的角度偏差都修正为0，只需对某一方向进行修正使得两方向的偏移角度值靠近图11所给出的曲线，系统就会变现出较好的响应特性。

(a) Ψ=0

(b) φ=0

(c) φ=Ψ=β

(d) -φ=Ψ=β图10 偏移角度对非线性度的影响Fig.10 Influence of deviation angular on the nonlinearity

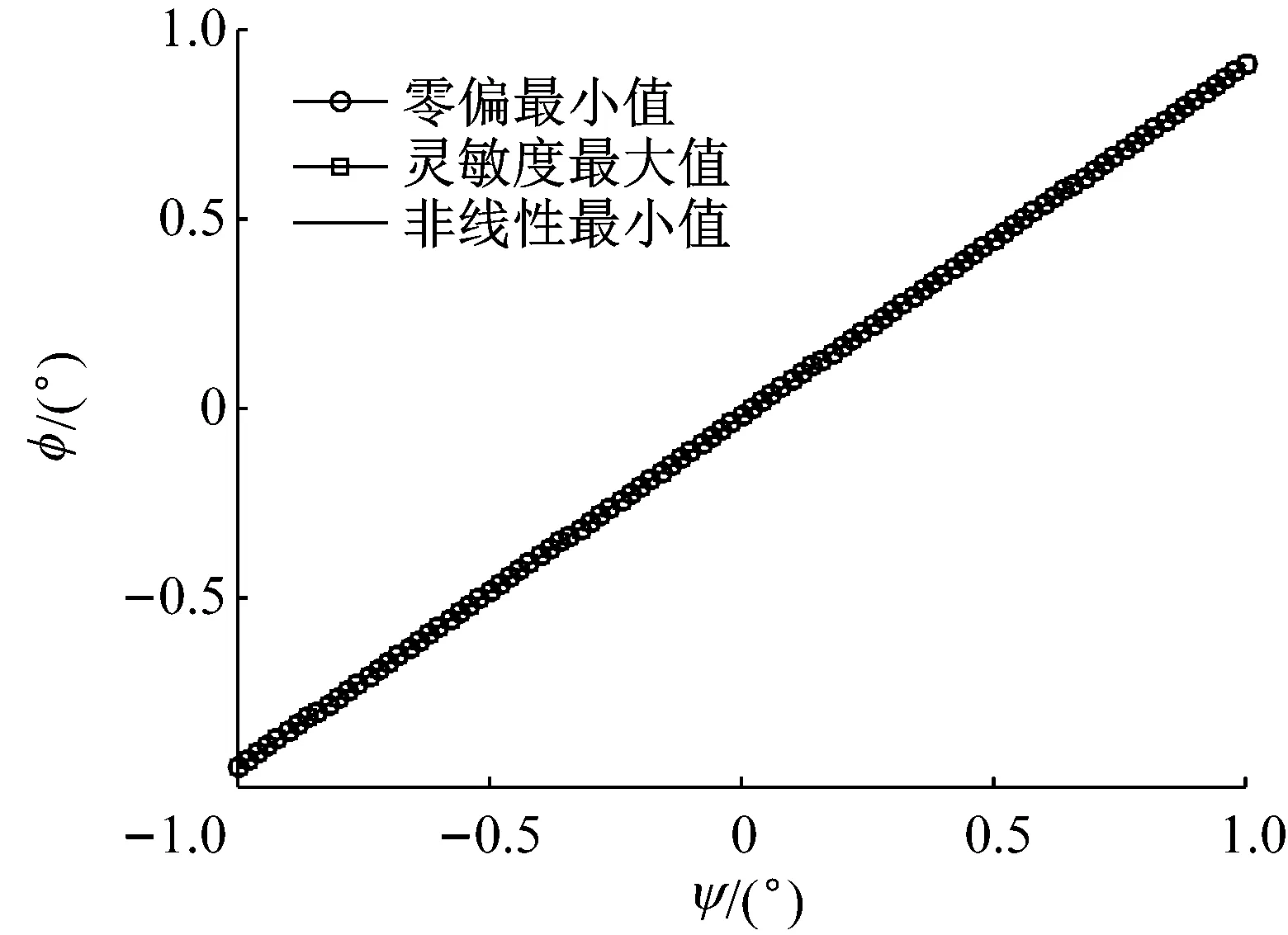
图11 零偏、非线性度取极小值，机械灵敏度取极大值 时偏移角度的关系曲线

Fig.11 The relation curves between deviation angles when zero bias, nonlinearity is minimized and the mechanical sensitivity is maximized

3 结 论

本文针对微机械陀螺系统加工误差对响应特性的影响，主要进行了如下工作：

(1) 考虑微陀螺系统的刚度非线性以及加工误差引起的弹性主轴和驱动/敏感轴之间的角度偏移的影响，通过拉格朗日方程求得了系统的动力学方程，利用平均法求得了关于系统振幅和相位的慢变方程。

(2) 采用同伦延拓方法分别研究了加工误差引起的角度偏移对微陀螺系统响应特性的影响，给出了偏移角度对零偏、机械灵敏度和非线性度影响的三维曲面，发现只有一个方向有角度偏移时，驱动或者敏感方向的角度偏移对三者的影响是相同的，即随着偏移角度绝对值的增大，零偏和非线性度增加，机械灵敏度降低。驱动和敏感方向同时有角度偏移时，沿两个偏移角度互为相反数的方向，零偏、机械灵敏度和非线性度随偏移角度大小的变化非常剧烈；而当偏移角度接近时，零偏、机械灵敏度和非线性度随偏移角度大小的变化较为平缓。

(3) 给出了系统零偏、非线性度取极小值，机械灵敏度取极大值时两个方向偏移角度之间的关系曲线，当偏移角度接近该曲线时，微陀螺系统的零偏、机械灵敏度和非线性度都较好。在工程中，对微机械陀螺敏感结构的修型并不需要将每个方向的角度偏差都修正为0，只需对某一方向进行修正使得两方向的偏移角度值接近该曲线即可。