热塑性复合材料原位成型过程铺层间结合强度

宋清华，刘卫平，刘小林，刘奎，杨洋，陈吉平

上海飞机制造有限公司，上海 201324

连续纤维增强热塑性复合材料自动铺放原位成型技术，是按照数模的要求，通过带有特殊装置的铺丝机进行定位、铺叠、压实和快速固结，在结构件厚度方向上逐层累加，达到设计的厚度时，完成结构件制造的工艺方法[1-4]。该技术大幅度减少了复合材料的制造工序，不需要再进热压罐，对模具要求降低，且热塑性预浸料可室温存放和使用[5-7]，从而降低复合材料结构件的材料成本和制造成本，该技术一旦成熟将会带来航空复合材料革命性的变化。但由于高性能热塑性树脂基体熔点高、熔融黏度大，原位成型过程需高温高压，且为了保证铺层聚合物分子链充分扩散及降低铺层孔隙率，需降低铺放速度从而保证铺层有足够的升温和加压时间[8-10]。虽然原位成型相比热压罐成型，已经提高了制造效率[11-13]，但目前原位成型的制造效率依然难以满足工程化需求，因此，需对原位成型的制造效率、结构件质量及工艺参数三者之间进行权衡，在保证原位成型结构件质量的前提下，通过成型工艺参数优化，提高原位成型制造效率，为连续纤维增强热塑性复合材料自动铺放原位成型技术工程化应用奠定基础。

强度测试是评价复合材料结构件质量的最重要手段之一，而原位成型的热塑性复合材料结构件的强度受铺层间结合强度的影响，因为铺层间结合强度的强弱将直接影响层间应力的传递效果。在原位成型过程中，铺层间结合强度就是铺放过程中相邻两层预浸料熔合后所能达到的层间强度，其大小受相邻两层预浸料紧密接触程度、熔合时分子链的扩散程度两方面因素影响，而这两方面因素又与自动铺放原位成型过程中铺层被加热的温度、加热时间、压辊压力及加压时间有关。

由于连续纤维增强热塑性预浸料表面粗糙度的存在，预浸料表面的微观形貌为不规则几何体(见图1)，因此在原位成型初始阶段，两层预浸料表面并没有完全接触，但随着激光热源的加热及压辊压力的作用下，两层预浸料的表面接触程度会逐渐发生变化。目前国外有比较多的数学模型和分析模型对一定条件两层预浸料间的接触程度进行分析研究。Dara和Loos[14]在建层间紧密接触度模型时将两相邻预浸料表面的微观几何形貌简化成不同尺寸的矩形(见图2)，但由于模型比较复杂，在实际求解过程中不方便计算；Lee和Springer[15]在Dara和Loos的模型基础上进一步进行了简化，将两层预浸纱的表面简化成规则周期排列的矩形，在压力的作用下，矩形发生规则变形且沿着界面扩展，如图3所示，图中b0为预浸纱表面简化矩形的原始长度；d0为预浸纱表面简化矩形凹槽的原始长度；h0为预浸纱表面简化矩形的原始高度；b1为预浸纱表面简化矩形发生规则变形后的长度；h1为预浸纱表面简化矩形发生规则变形后的高度。Lee和Springer的紧密接触度模型只考虑了压力和加热温度的影响，但原位成型过程中预浸料两表面之间的接触是个动态的过程，因此考虑到铺层间接触的时效性，本文在Lee 和Springer 模型的基础上，建模分析自动铺放原位成型过程中两相邻预浸料表面的加热温度、加热时间、压辊压力及加压时间对紧密接触度的影响。

图1 预浸料相邻接触面原始不规则微观形貌Fig.1 Original irregular microscopic appearance of contact surface for prepreg

图2 Dara和Loos简化后不规则微观形貌[14]Fig.2 Irregular microscopic appearance simplified by Dara and Loos[14]

图3 Lee和Springer简化后规则微观形貌[15]Fig.3 Regular microscopic appearance simplified by Lee and Springer[15]

原位成型过程中，在相邻两铺层紧密接触之后开始熔合在一起，所谓熔合，就是指预浸料树脂基体熔融后，并在压辊压力的作用下，相邻两层预浸料紧密接触部分之间分子链扩散的现象，且分子链的扩散程度将直接决定铺层间的结合强度。国外目前关于分子链扩散的研究，大多基于链的塌滑理论。Wool和O’connor[16]为分子链在层间的扩散建立了分子链运动模型，认为界面间分子链的纠缠和层内分子链的纠缠效果一样，都是阻碍了分子链的运动；Kim和Wool[17]证明了层间结合强度与分子链的扩散距离成正比，当扩散时间无限长的时候，分子链能得到充分扩散，则层间结合强度越接近最大值；但Wool等[18]又指出实际用到的工程塑料，分子量远大于8倍临界纠缠分子量，因此分子链的扩散距离达不到最大值。上述学者的研究都是从传统的分子链扩散理论出发进行分析研究，而由于高性能聚合物熔融黏度大，分子链的扩散速度比较慢，因此严重影响制造效率。本文在铺层紧密接触模型基础上，建立高温下分子链的扩散模型，研究原位成型过程中分子链的扩散与成型工艺参数之间的关系，通过工艺参数优化，增大分子链的扩散速度，从而提高原位成型制造效率。

1 原位成型过程中层间结合强度模型

1.1 紧密接触模型

连续纤维增强热塑性复合材料自动铺放原位成型过程中，相邻两铺层间的紧密接触程度用紧密接触度Dic表示，所谓紧密接触度，就是原位成型过程中，在任意时刻相邻两层预浸料的接触面积占总面积的百分数。Lee和Springer建立的紧密接触模型没有考虑原位成型过程铺层间接触的时效性，因此本文在Lee和Springer模型基础上，将模型中规则矩形的长度和高度变化用时间函数来描述，如图4所示，图中b(t1)为在温度和压力作用下预浸纱表面简化矩形凸起的长度随时间t1的变化；h(t1)为预浸纱表面简化矩形凸起的高度随时间t1的变化。因此紧密接触度可表示为

(1)

假设在原位成型过程中，预浸纱表面简化矩形的体积保持为常数不变，可以推导出紧密接触度的表达式为[19]

(2)

目前为获得预浸料表面的微观几何形貌尺寸，大多采用测量的方法，用测量的方法获得的数据样本不仅有限还不具有普遍性，因此通过将粗糙度Rc引入紧密接触度模型[20]，用预浸料表面粗糙度的数值评价预浸料表面微观几何形貌，即

(3)

因为原位成型过程铺层间的接触是瞬态过程，因此需将式(3)中的时间离散化，则紧密接触度的模型可修正为

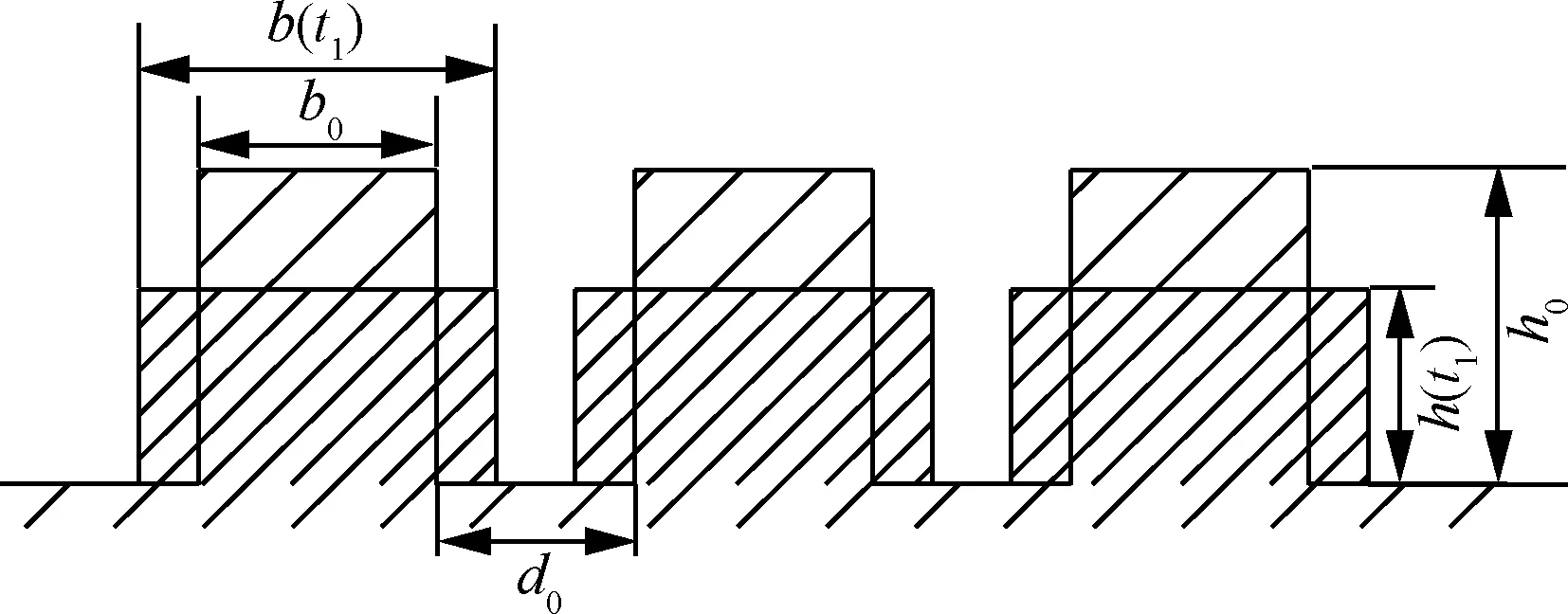
图4 简化后与时间相关的规则微观形貌Fig.4 Time-related regular microscopic appearance simplified by this paper

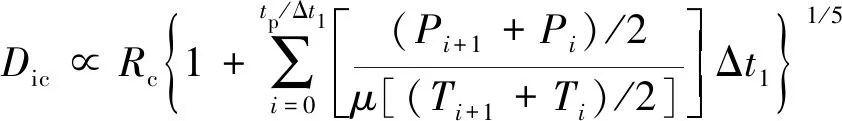
(4)

式中:Δt1为离散化的瞬时时间变化；Pi为离散化的瞬时压辊压力；Ti为离散化的瞬时温度。

所以，在已知预浸料表面粗糙度及不同温度下树脂基体的黏度基础上，由式(4)可以计算出原位成型过程中两相邻铺层的紧密接触度与铺放速度及压辊压力之间的关系。

1.2 分子链扩散模型

对于半结晶热塑性复合材料，当温度高于玻璃化转变温度(对于晶体部分温度需高于熔点)，界面间的分子链开始相互扩散，从而提高铺层间的结合强度。传统的蠕动理论认为分子链的扩散距离随着时间的延长而增大[17]，因此

(5)

式中:χ为分子链的扩散距离；t2为分子链的扩散时间；M为分子质量。

根据Kim和Wool[17]证明的层间结合强度与分子链的扩散距离成正比的理论，可得

(6)

式中:σ为层间剪切强度(InterLaminar Shear Strength,ILSS)。

假设分子链充分扩散后的层间结合强度为σ∞，则最大的层间结合强度可表示为

(7)

式中:tr为一定温度下分子链的充分扩散时间。

因此，分子链的扩散程度Dr可以用层间结合强度的比值来表示：

(8)

从式(8)可以看出，铺层的层间结合强度与分子链扩散时间的1/4成线性关系。

因此，针对原位成型过程铺层非等温升温的特点，通过修正式(8)，得到了分子链扩散程度的积分模型为

(9)

式中:tw为分子链扩散所需要的时间；T为加热温度。

对于分子链的扩散过程，分子链运动的温度依赖性服从Arrhenius方程，所以分子链的扩散时间可表示为

(10)

式中:τ0是一个常数；R为气体常数；ΔE为分子链扩散所需要的活化能。

因此，从式(10)可知分子链的扩散时间取决于分子运动活化能和加热温度，而对于给定的聚合物，其活化能ΔE大致为一常数，因此分子链的扩散时间主要依赖于加热温度。为提高原位成型制造效率，必须解决的关键问题之一就是提高分子链的运动速度，故本研究通过提高原位成型过程铺层的升温速率，使铺层温度迅速升高，从而使聚合物分子链单元的动能增加，使其迅速活化，缩短分子链的扩散时间，从而在提高铺放速度的同时，还保证铺层间的结合强度。

2 层间结合强度模型计算输入参数的确定

本研究所选材料为连续碳纤维增强聚苯硫醚复合材料(Carbon Fiber / PolyPhenylene Sulfide, CF/PPS)，其DSC曲线如图5所示。从图中可以看出，PPS树脂基体起始熔化温度为270.6 ℃，293.4 ℃时达到顶峰，温度达到304.7 ℃时，树脂基体熔化基本结束。

图6为不同升温速率下CF/PPS预浸料的热失重曲线。从图中可以看出，PPS在热解过程中仅存在一个明显的热失重平台，在程序升温过程中，不同升温速率的TG曲线基本一致，说明在不同升温速率下，CF/PPS的热分解过程相类似。由TG曲线可以发现，升温速率对CF/PSS的热失重影响较大，随着升温速率的提高，TG曲线向高温方向移动，当升温速率为200 ℃/min时，CF/PPS预浸料的降解起始温度为540 ℃，而PPS树脂理论降解温度为440 ℃，所以通过提高升温速率的方式，不仅可以快速升高预浸料被加热的温度，还可以扩大预浸料的工艺窗口。

图5 CF/PPS熔化过程动态扫描DSC曲线Fig.5 Curve of melting process dynamic scanning DSC for CF/PPS

图6 不同升温速率下CF/PPS的热失重曲线Fig.6 Thermal degradation curves of CF/PPS for different heating rates

由CF/PPS复合材料激光加热原位成型过程温度场分析[21]可知，当激光加热功率选择3 kW，铺放速度为12 m/min时，铺层被加热的升温速率大概为9 000 ℃/min，远远大于TG试验中的200 ℃/min，所以根据TG曲线随着升温速率的变化规律，理论上铺层树脂基体的瞬时降解温度在540 ℃以上。本研究在保证原位成型结构件质量的前提下，为尽可能提高制造效率，所以选择激光最大输出加热功率 6 kW，铺层树脂基体降解温度设为540 ℃。同样，由文献[21]可知，当激光加热功率选择6 kW时，合理的铺放速度为6 m/min到45 m/min，同时可计算出不同铺放速度对应铺层被加热的峰值温度。

图7为PPS树脂基体的黏度-温度曲线，从图中可以看出，当加热温度超过PPS的熔点后，PPS的黏度随着温度的升高不断降低；可根据图7获得不同温度下PPS树脂基体的黏度值。

图8为本研究试验所用的激光加热自动铺放原位成型设备。该设备最大压辊压力为1 000 N，因压辊为柔性压辊，所以随着铺放压力的改变，压辊变形量也在发生变化，为简化计算，本研究认为随着压辊压力的变化，压辊与铺层表面的接触长度始终保持在25 mm。

本研究计算层间结合强度模型时所需的其他参数如表1所示。其中，表面粗糙度Rc通过Starrett-SR200型便携式表面粗糙度测试仪测得，如图9所示。

图7 PPS树脂基体的黏度-温度曲线Fig.7 Viscosity-temperature curve for PPS resin matrix

图8 激光加热自动铺放原位成型设备Fig.8 Laser heating AFP in-situ consolidated equipment

表1 层间结合强度模型计算相关参数

Table 1 Correlation calculating parameters for

laminar strength model

参数变量数值单层厚度/mmd0.14铺层总数N16表面粗糙度/μmRc0.23分子链扩散时间常数/sτ00.11[22]气体常数/(J·mol-1·K-1)R8.314活化能/(kJ·mol-1)ΔE20[22]铺放速度/(m·min-1)v6～45激光加热功率/kWQ6压辊压力/NP1000

图9 CF/PPS预浸料表面粗糙度Rc测量过程Fig.9 Measuring process of surface roughness Rc for CF/PPS

3 计算结果分析与试验验证

图10所示为铺放速度及铺放压力对铺层间紧密接触的影响。从图中可以看出，随着铺放速度的增加，铺层间的紧密接触度逐渐降低；随着压辊压力的增大，铺层间的紧密接触度逐渐升高。通过对比发现，铺放速度对铺层紧密接触度的影响要小于压辊压力对紧密接触度的影响。这是因为当铺层被加热的温度高于玻璃化转变温度(对于晶体部分温度需高于熔点)时，树脂即可发生变形，但铺层间的紧密接触度受预浸料表面粗糙度及孔隙等因素的影响，而这些影响因素均需压辊压力克服，所以压辊的压力对铺层间的紧密接触度影响较大。但通过计算发现，即使选择最大压辊压力1 000 N，铺层间的紧密接触度依然难以达到最大值1，这意味着试验设备的压力并没有达到要求。通过式(4)可以计算出，当压辊压力达到1 500 N时(图中虚线所示)，铺层间的紧密接触度才接近最大值1。

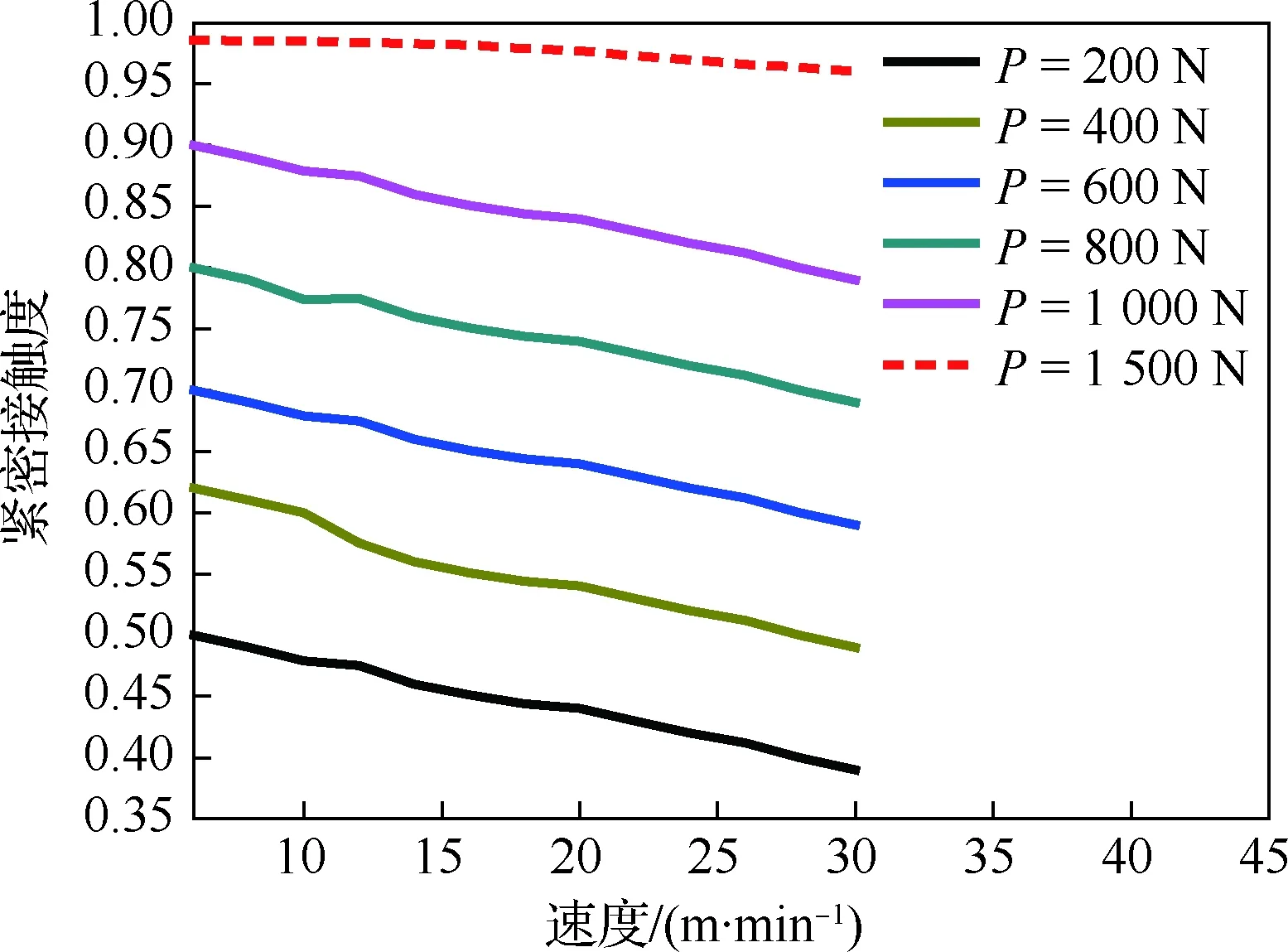
图10 不同铺放速度及压辊压力作用下 铺层紧密接触度的变化Fig.10 Development of intimate contact with variations of AFP speed and pressure of roller

本研究选择压辊压力的最大值1 000 N，研究铺放速度对分子链扩散程度的影响，如图11所示。从图中可以看出，随着铺放速度的增大，分子链的扩散程度逐渐降低，且铺放速度越快，分子链扩散程度越低。这是因为在低速下，铺层被加热时间长，树脂基体被加热温度高，降低了树脂基体的黏度，缩短了分子链的扩散时间，从而提高分子链的扩散程度。当铺放速度为6～12 m/min时，铺层被加热的温度足够高，因此分子链的扩散程度变化不大；但当铺放速度高于12 m/min时，由于铺层被加热温度相对较低，导致分子链的扩散程度迅速降低。同样通过计算可以发现，最大的分子链扩散程度也只有85%左右，这也意味着分子链所需扩散时间比计算时间更长，所以还需进一步降低铺放速度或提高铺层的加热温度，延长分子链的扩散时间。通过计算可以发现，当铺放速度为1 m/min时，铺层聚合物的分子链扩散程度才接近1(图11中虚线部分)，但1 m/min的铺放速度显然难以满足工业化需求。

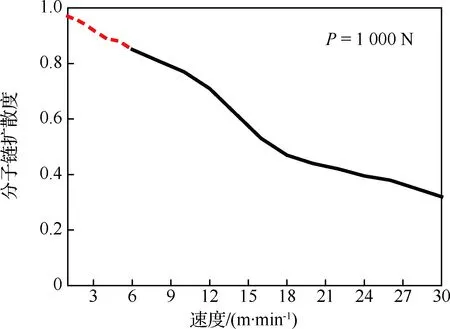
图11 不同铺放速度下分子链扩散程度变化Fig.11 Development of chain diffusion with variations in AFP speed

为验证本研究所建立的层间结合强度模型的正确性，将原位成型后的平板试片选择部分进入高温高压热压罐进行后处理，如图12所示。热压罐有效工作尺寸：∅1 m×2 m；最高工作温度：400 ℃；温度均匀性：250 ℃以下，≤±2 ℃，250～400 ℃，≤±3 ℃；最高压力3.5 MPa，加热速度0.1～5 ℃/min，冷却速率0.5～6 ℃/min。

CF/PPS复合材料的热压罐制备工艺流程如图13所示。真空袋全程抽真空，罐内温度从室温起以5 ℃/min升至试验设计温度T′=332 ℃，罐内压力从常压起加至试验设计压力P′=1.75 MPa；在试验设计温度T′下保温时间为t′=23 min，然后以6 ℃/min 降至室温，再卸压、出罐。

图14为原位成型和经热压罐后处理后的CF/PPS复合材料试片按标准ASTM D 2344/D 2344M-00[23]测试的层间剪切强度随铺放速度的变化关系。因热压罐加热加压时间充足，聚合物分子链可以充分扩散，本研究认为经热压罐处理的CF/PPS试片的层间结合强度能达到最大值。因此以热压罐成型试片的性能作为参考(矩形图标曲线)，根据图11分子链扩散模型的预测结果，可得到图14中铺层间结合强度预测结果(圆形图标曲线)。三角形曲线为原位成型试片的层间剪切强度测试结果。

图12 高温高压热压罐Fig.12 High temperature and high pressure autoclave

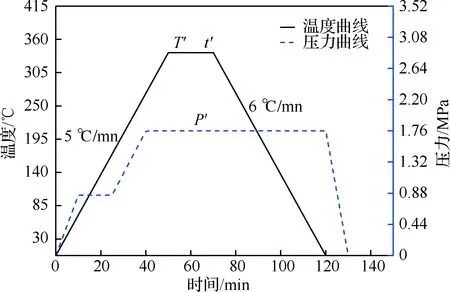
图13 CF/PPS复合材料热压罐制备工艺流程Fig.13 Autoclave forming process for CF/PPS composite material

图14 铺放速度对CF/PPS试片层间剪切强度的影响Fig.14 ILSS with variations in ATP speed for CF/PPS laminate

从图14可以发现，随着铺放速度的增加，原位成型试片的性能逐渐降低，与分子链扩散模型的预测结果基本一致，但原位成型试片的性能略低于模型的预测结果，这说明原位成型试片的性能不仅取决于分子链的扩散程度，还受其他因素的影响，比如结晶度等，但本研究建立的层间结合强度模型的预测结果与原位成型试验结果基本吻合，说明建立的模型对原位成型过程工艺参数的选择有一定的参考意义；由于热压罐成型过程中加热加压时间充足，故热压罐成型后试片的性能随铺放速度的变化几乎保持不变，但在低速下，性能会偏低，这是因为在激光高加热功率下，铺层被加热的温度过高，铺层发生降解，导致成型试片性能下降；同样的现象也出现原位成型试片的层间剪切强度测试曲线中，在铺放速度6～12 m/min变化时，成型试片的ILSS出现略微升高的趋势，在10～12 m/min成型试片的性能几乎保持不变，当铺放速度超过12 m/min时，试片的性能迅速下降。

故研究结果表明，原位成型过程中，当选择最大激光加热功率6 kW时，合适的铺放速度为10～12 m/min；通过测试结果可以发现，原位成型试片的性能最大值仅达到热压罐成型的70%左右，因此还需对原位成型试片性能的其他影响因素进行分析，比如结晶度等，另外，在设备允许的情况下，可以增加压辊的压力及适当降低铺放速度，但降低铺放速度会使铺层聚合物在高温下停留时间变长，导致铺层聚合物发生降解，因此为权衡加工效率与成型试片质量之间的关系，还需进一步对原位成型过程中铺层聚合物的降解行为进行分析，以获得更优的铺放工艺参数及成型试片的性能。

4 结 论

1) 为研究原位成型过程铺放工艺参数对成型试片性能的影响，首先通过引入预浸料表面粗糙度，建立原位成型过程铺层间紧密接触模型，研究铺放速度及压辊压力对铺层间紧密接触度的影响。结果表明铺放速度对层间接触度的影响不大，而铺放压力达到1 500 N时，铺层间的紧密接触度才能达到1。

2) 其次，建立铺层间分子链的扩散模型，从模型中发现可以通过快速升温的方式缩短分子链的扩散时间，从而提高铺放速度。结果表明，在选择本研究最大压辊压力1 000 N时，合适的铺放速度为6～12 m/min，但分子链的最大扩散度也仅为85%左右。

3) 最后，为验证建立层间结合强度模型的正确性，对原位成型及热压罐成型试片的层间剪切强度进行测试。试验结果表明，层间结合强度模型的预测结果与原位成型试验结果基本吻合；但原位成型试片的性能最大值仅达到热压罐成型的70%左右，因此还需对原位成型试片性能的其他影响因素进行分析，比如铺层聚合物的结晶行为及降解行为进行分析。