直觉模糊熵改进的公理化定义和计算公式

郑婉容, 郑婷婷，张毛银

(安徽大学 数学科学学院, 合肥 230601)

0 引 言

通常情况下，现实世界有很多东西分类都是模棱两可，没有明确的界限，这样就容易出现模糊性概念.Zadeh[1]的模糊集理论在1965年被提出来，它对于一些不确定性问题可以提供很多的依据；1986年，Atanassov[2]给出直觉模糊集.对于刻画它们的不确定性，相应的熵理论也快速发展起来.

1972年，模糊熵的公理化定义被Deluca和Termini[3]共同提出.直觉模糊熵公理化定义是由Bustince H和Burillo P[4]最早开始给出.由于这个定义的应用不能广泛推广，有一定的限制，2001年，Szmidt[5]修改了这个定义，运用几何知识提出直觉模糊熵公式.文献[6]提出一些新的相关概念，讨论了已有的公理化定义存在的问题并且进行了修改，在满足改进的公理化定义的基础上给出一个新的直觉模糊熵公式.在文献[7]中指出文献[8]中公理化的缺陷，提出新的公理化定义与公式并且将其应用到决策中.Ye[9]利用三角函数这个数学概念给出两个直觉模糊熵公式，但这两个公式所考虑的变量问题过于片面，即没有考虑犹豫度，仅仅涉及模糊集的隶属度和非隶属度之间的差异，不能完整反映出直觉模糊程度.此处提出修改过的公理化定义和公式，并证明了新的公式符合修正过的公理化定义.

1 模糊熵的公理化定义

定义1[10]∀A，B∈F(X)，其中F(X)为论域X上的模糊子集的全体.

映射：H：F(X)→[0，1]，则模糊集的模糊熵H满足下面约束：

① ∀x∈X，μA(x)∈{0，1}⟺H(A)=0；

② ∀x∈X，μA(x)≡0.5⟺H(A)=1；

③ ∀x∈X，μB(x)≤μA(x)≤0.5或

μB(x)≥μA(x)≥0.5⟺H(B)≤H(A)；

④ ∀A∈F(X)，H(A)=H(Ac).

度量模糊集的模糊程度是采用隶属度这个变量，为了度量直觉模糊集的模糊程度，要考虑其含有的变量基础上，提出相应的公理化定义.

2 直觉模糊熵的公理化定义

定义2[3]设X为一个集合，μA：X→[0，1]，vA：X→[0，1]，满足：

μA(x)+νA(x)≤1，∀x∈X

则称A=(X，μA，νA)为X上的一个直觉模糊子集，且记A(x)=(μA(x)，νA(x))，其中μA(x)为元素x对A的隶属程度，νA(x)为元素x对A的非隶属程度.

直觉模糊集A的补集记为Ac，即

Ac={〈x，vA(x)，μA(x)〉|x∈X}

当直觉模糊集A=(X，μA，νA)，满足μA(x)+νA(x)=1，∀x∈X，即A退化为Zadeh模糊集.

下面给出两个预备知识：

在直觉模糊集A中，由于隶属度和非隶属度相加不等于1并且代表x对于一个A属于或不属于关系是确定的，现在想要将不等号改为等号，就需要加入一个新的变量即犹豫度使之达到平衡，该变量反映了直觉Fuzzy集的不确定性.

定义3 ∀x∈X，记πA(x)=1-μA(x)-νA(x)，0≤πA(x)≤1，那么称πA(x)为x属于A的犹豫度.

注1直觉Fuzzy集退化成Fuzzy集的充要条件是πA(x)=0.

在直觉Fuzzy集A中，由于μA(x)和νA(x)没有明确的大小比较，而新定义的变量即核要求是大于0的，不能为负数，所以需要加一个绝对值.

定义4∀x∈X，记SA(x)=|μA(x)-νA(x)|，0≤SA(x)≤1，那么称SA(x)为x属于A的核.

2001年，Szmidt E和Kacprzyk J提出了直觉模糊熵的新的公理化定义.

定义5[5]设E：IFS(X)→R+为一个映射，E为IFS(X)上的熵，即有E如下：

①E(A)=0⟺A为分明集；

②E(A)=1⟺∀x∈X，μA(x)=νA(x)；

③ ∀x∈X，当μB(x)≤νB(x)时，有μA(x)≤μB(x)且νA(x)≥νB(x)，当μB(x)≥νB(x)时，有μA(x)≥μB(x)且νA(x)≤νB(x)，则E(A)≤E(B)；

④E(A)=E(Ac).

注2定义5中，直觉模糊熵只采用了μA(x)和νA(x)，忽略了πA(x)，因此不予推广.

H-Y公理化定义[8]是考虑μA(x)+νA(x)+πA(x)=1，∀x∈X成立，但是由于概率是随机事件发生可能性的大小，其值在0到1之间，事件确定不发生的概率是0，确定发生的概率为1，这样就与μA(x)，νA(x)和πA(x)的概念存在着偏差，不能将两者混淆，因此不能将这3个变量作为概率测度.

完整地考虑μA(x)，νA(x)，πA(x)这3个变量的关系，补充条件，提出了一个新的直觉模糊熵公理化定义：

定义6 ∀A，B∈IFS(x)，称映射E：IFS(x)→R+为IFS(X)上的熵，即E有如下性质：

①E(A)=0⟺A为分明集；

②E(A)=1⟺∀xi∈X，μA(x)=νA(x)成立；

③E(A)是关于SA(x)=|μA(x)-νA(x)|的单调减函数，是关于πA(x)=1-μA(x)-νA(x)的单调增函数；

④E(A)=E(Ac).

定义6中，性质①说明当直觉Fuzzy集退化成普通集时，即是明确集；性质②说明直觉模糊熵为1的充要条件是μA(x)与νA(x)没有差值；性质③说明直觉模糊熵是SA(x)和πA(x)函数，即πA(x)=πB(x)，SA(x)≤SB(x)时，E(A)≥E(B)；SA(x)=SB(x)，πA(x)≤πB(x)时，E(A)≤E(B).性质④说明A与其补集Ac的模糊程度一样.

3 现有直觉模糊熵存在的问题

魏翠萍等[12]证明出Ye[9]给出的两个直觉模糊熵是等价的，即

证出

J1(A)=J2(A)=

(1)

由此可见式(1)只考虑μA(x)和νA(x)之间的关系，没有考虑πA(x)，因此与直觉不符.

Burillo[13]等提出的直觉模糊熵为

(2)

式(2)与上面的式(1)相反，仅仅考虑πA(x)的变化，其模糊性没被考虑，因此不能作为直觉模糊集的不确定性度量.

4 新的直觉模糊熵公式

定理1 设论域X={x1，x2，…，xn}，A={〈xi，μA(xi)，νA(xi)〉|xi∈X} 是X上的直觉模糊集，则定义直觉模糊熵：

证明要证明式(3)是直觉模糊熵，只需要证明该式满足定义6的4个条件即可，令

由于0≤μA(xi)≤1，0≤νA(xi)≤1，0≤πA(xi)≤1，则可以得到：

也即

因此0≤Ei(A)≤1，得到0≤E(A)≤1.

1)若E(A)=0，由于0≤Ei(A)≤1，可以得到Ei(A)=0.

若A为分明集时，∀xi∈X，有μA(xi)=1，νA(xi)=0或μA(xi)=0，νA(xi)=1，则有Ei(A)=0，即E(A)=0.

2)∀xi∈X，有μA(xi)=νA(xi)，可得Ei(A)=1，即E(A)=1.

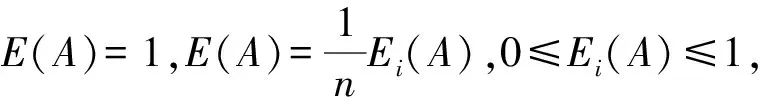
3)令SA(x)=|μA(x)-νA(x)|=x，πA(x)=1-μA(x)-νA(x)=y，其中0≤x≤1，0≤y≤1.

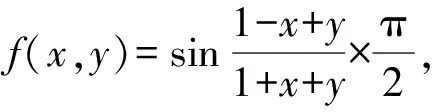
则E(A)关于SA(x)=|μA(x)-νA(x)|=x是单调减函数，关于πA(x)=1-μA(x)-νA(x)=y是单调增函数.

4)E(Ac)=

例1 计算直觉模糊集

A1={〈xi，0.1，0.3〉|xi∈X}

A2={〈xi，0.2，0.4〉|xi∈X}

A3={〈xi，0.2，0.5〉|xi∈X}

A4={〈xi，0.4，0.3〉|xi∈X}

的直觉模糊熵.

解利用Ye提出的直觉模糊熵公式得到：

可以看出对于直觉模糊集A1和A2来说，它们的犹豫度πA1(xi)≠πA2(xi)，但J(A1)=J(A2)，显然与直觉不符.

利用Burillo等给出的直觉模糊熵公式：

得到E(A1)=0.6，E(A2)=0.4，E(A3)=0.3，E(A4)=0.3.对于直觉模糊集A3和A4来说，E(A3)=E(A4)，可以看出忽略了μA(x)与νA(x)的差异，因此与直觉不符.

现在利用新的直觉模糊熵公式得到：

由此可见，在两个直觉模糊集的核SA(x)= |μA(x)-νA(x)| 相同的时候，其犹豫度越大，说明这个直觉模糊集的模糊程度越高，则对应的熵越大，即E(A1)

5 结 论

模糊熵本身只是简单的考虑隶属度和非隶属度这两个变量的一系列相关变化，即使这样对于它的研究也是很艰难的.而直觉模糊集是在模糊集的基础上发展起来的，对应的直觉模糊熵是在模糊熵的基础上又考虑了犹豫度，因此对于直觉模糊熵的深入研究变得更加深奥.多年来对于直觉模糊熵的公理化定义和公式被诸多学者所提出，由于当时知识水平具有一定的局限性，这些定义和公式出现了各种各样的不足而未能被广泛推广.在前人研究的基础上，对已有公理化定义和公式进行总结与修改，提出改进的定义，同时利用数学中的正弦函数的概念提出新的公式，算例表明新的公式符合人们的认知.