带Markov切换的随机微分系统的输入状态稳定性*

王 刚，吴小太

(安徽工程大学 数理学院，安徽 芜湖 241000)

0 前 言

稳定性问题一直以来都是系统控制理论研究的热点问题，输入状态稳定作为一类重要的稳定性，受到了学者们的广泛关注。输入状态稳定(Input-to-state stability)理论由Sontag教授于1989年在文献[1]中提出，它表明：无论系统初始状态的大小如何，系统最终状态将趋近其初值的某一邻域且与外部输入的大小成比例。近来，关于系统输入状态稳定的相关研究受到很多学者的重视，并得到了丰富的研究结果。Wang等在文献[2]中基于分段Lyapunov-Krasovskii函数方法，研究了非线性脉冲系统的输入状态稳定性问题；文献[3]研究了非线性脉冲混合随机系统的输入状态稳定性问题；通过建立一个有效引理，Ai等[4]构造了一类广义KL函数，研究了带脉冲切换的随机非线性脉冲系统有限时间随机输入状态稳定性；Wu等[5]利用Lyapunov-Krasovskii函数和平均脉冲间隔法，分别推导出了基于线性假设的稳定和不稳定脉冲随机时滞系统的输入状态稳定性条件；Kuang等在文献[6]中提出了一种用于研究随机时滞控制系统的均方指数输入状态稳定性Euler-Maruyama法；文献[7]利用多Lyapunov 函数方法，研究了带切换的离散时间非线性系统的全局渐近稳定性和输入状态稳定性。

随机切换系统是由随机微分系统与切换规则构成的动态系统[8-10]。Markov切换系统是由连续时间的马氏链驱动的一类重要的随机切换系统，在相关的理论研究中运用最为广泛，并已被应用于许多结构和参数可能会突然改变的实际系统模型中，如电力系统、太阳能系统和战斗管理指挥、控制和通信系统等[11]。Wu X等在文献[12]中利用Razumikhi型方法，获得了一些稳定性判据，从而进一步发展了带Markov切换的脉冲随机时滞微分系统的p阶矩稳定性；文献[13]利用切换过程的跳转时间来细分”时间”，讨论了带Markov切换的非线性随机微分方程的渐近稳定性；通过M矩阵方法，文献[14]研究了带Markov切换的随机变时滞神经网络系统的均方指数稳定性；针对状态切换跳扩散系统，宗小峰[15]利用文中结果结合马氏链的遍历性，给出了p阶矩指数稳定性的条件。

本文借助文献[15]中关于马氏链遍历性的新定义，研究了带Markov切换的随机微分系统的输入状态稳定性。值得注意的是，当文中外部输入为零时，输入状态稳定性即为渐近稳定性，故本文的研究结果能包含文献[15]中的定理4.12。

相关记号：

ξ={ξ(v)：-θ≤v≤0}

使得

E表示期望算子，令K为一族连续严格增长的函数k：R+→R+，k(0)=0，K∞为K函数的无界子集，函数β：R+×R+→R+属于集合KL。

1 相关定义与引理

令(Ω，F，Ft≥0，P)为一个完备的概率空间，域流Ft≥0满足一般情况(其为右连续增长的，且F0包含所有不可测集)。令B(t)，t≥0为定义在概率空间上的m-维布朗运动，r(t)，t≥0为一个取值在有限状态空间S=1，2，…，N上的右连续，且定义在概率空间的Markov链，其生成元Γ=(γij)N×N由

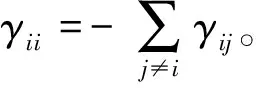
本文将考虑如下带Markov切换的非线性随机微分系统：

dx(t)=f(xt，u(t)，r(t))dt+

g(xt，u(t)，r(t))dB(t)，t≥t0

(1)

若f与g都服从局部Lipschitz条件以及线性增长条件，则在该条件下系统式(1)拥有唯一解x(t)[9]。本文为了研究系统的稳定性，假设f(0，0，i)≡0，g(0，0，i)≡0，系统式(1)有平凡解x(t)≡0。

给定任意V∈C2，1(Rn×[t0，+R)，定义下述映射LV，以下有Rn×R+×S→R。

LV(x，t，i)=Vt(x，t)+Vx(x，t)f(x，t，i)+

为了得到本文中所研究的主要结果，需要给出一些必要的定义与引理。

定义1[5]系统式(1)为输入状态稳定(ISS)的，则存在函数β∈KL与γ∈K∞使得

E|x(t)|≤β(|x(t0)|，t-t0)+γ(‖u‖[t0，t])，t≥t0

定义2[15]令P为状态空间S的概率测度集，马氏链r(t)拥有式(2)给定的概率函数：

(2)

p=(p1，…，pm)∈P为一个概率向量，u=(u1，…，um)∈Rm，易得I(p)≥0为弱半连续的，当且仅当p=π时，I(p)=0，则

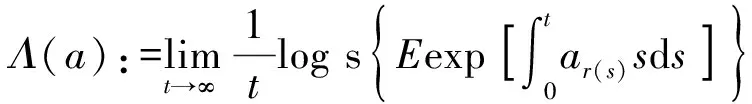
a=(a1，…，am)∈Rm

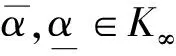
(H2)当|x|≥χ(u)时，有LV(x，t)≤αiV(x，t)。

2 主要结论

这里将研究带Markov切换的非线性随机微分系统的输入状态稳定性。

定理1 假设带Markov切换的非线性随机微分系统式(1)存在一个输入状态稳定的Lyapunov函数V(x，t)，使得

(3)

则系统式(1)满足输入状态稳定性。

如果l取有限值，则这一个区间的长度是无限的，此时可以采用文献[15]中的方法进行类似地处理，下面将分两种情况

①Λ1={t|x(t)|≥φ(‖u‖[0，t])，t≥0}；

②Λ2={t|x(t)|≤φ(‖u‖[0，t])，t≥0}。

来研究系统式(1)的输入状态稳定性。

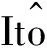
e-αr(τk∧ρn)(t∧ρn)V(x(t∧ρn))=

e-αr(τk∧ρn)(τk∧ρn)V(x(τk∧ρn))+

LV(x(s)，r(s))]ds+

e-αr(τk∧ρn)(t∧ρn)V(x(t∧ρn))≤

(4)

令Ft=σ{r(u)u≥0，{B(s)}s≥t}为随机变量{r(u)u≥0}，{B(s)}s≤t生成的右连续σ域流，这里定义的σ域流Ft满足一般性，系统式(1)的解x(t)关于域流Ft适应，由于ρn是一个Ft停时，以及解x(t)的右连续性，因此，其是一个关于Ft适应的过程。

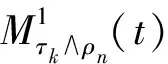
E[e-ηr(τk)tV(x(t))|Fτk]≤e-ηr(τk)τkV(x(τk))

表示E[V(x(t))|Fτk]≤eαr(τk)(t-τk)V(x(τk))，接下来，得到：

E[V(x(t))|Fτk-1]≤eαr(τk)(t-τk)E[V(x(τk))|Fτk-1]≤

(5)

注意到

EV(x(t))≤

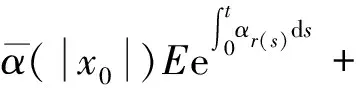
(6)

EV(x(t))≤ϑφ(‖u‖[0，t])

(7)

故由式(5)与式(7)知，式(6)成立。

根据(H1)与式(6)，有

即有

β(|x0|，t)+γ(φ(‖u‖[0，t]))

这里，

由式(2)知，β(x，t)∈KL，于是，随机微分系统式(1)满足输入状态稳定性。