鲁棒凸多目标优化问题解集的刻画*

郑 霜，周俊屹

(重庆师范大学 数学科学学院，重庆 401331)

单目标数学规划问题最优解集的刻画方法对理解具有多重最优解的数学规划问题的解法具有重要的作用.众所周知，对于各种类型的数学规划问题解的刻画[1-5]，通常假定程序的输入量或输入数据是精确的.然而，实际生活中优化问题的目标函数通常是多个的情形，并且由于预测或测量误差，导致与目标函数和约束函数相关的输入数据通常是不确定或不完整的[6-7].因此，研究此类不确定多目标优化问题就显得尤为重要.近几年，单目标鲁棒对应问题中与最优解集刻画相关的问题和对偶等性质已被广泛研究[6-10],并且多目标优化理论与方法的研究已有大量重要的研究成果[11-17].

受参考文献[8]中研究方法的启发，本文研究不确定凸多目标规划的鲁棒G-真有效解集的刻画.首先研究的是不确定凸多目标鲁棒对应问题的标量化问题中一般化的常微分性质和常拉格朗日性质，再利用这些性质最后得到该标量化问题的鲁棒解集的刻画.

1 预备知识

考虑如下这个多目标优化问题：

s.t.gj(x)≤0，j∈J={1，2，…，m}

然而，在实际问题中，由于预测或测量的误差[6-7]导致与目标和约束相关的输入数据通常是不确定或不完整的.因此对于以上模型，目标函数和约束函数在面对数据不确定时可以改为如下参数化模型：

s.t.gj(x，vj)≤0，j∈J

受参考文献[14]的启发研究给定一个解点的鲁棒G-真有效解集的刻画问题，这种方法需要用到如下的多目标鲁棒对应形式：

s.t.gj(x，vj)≤0，vj∈Vj，j∈J.

令

将(RMOP)标量化为如下单目标鲁棒优化模型(SP)λ，其中取定一个

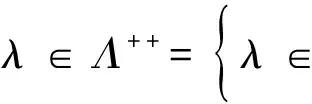
s.t.gj(x，vj)≤0，vj∈Vj，j∈J

近几年，这种鲁棒单目标优化问题解点的刻画，对偶性质和计算处理性在参考文献[6-9]中已被广泛研究.

定义1[14-15]

(1)(鲁棒可行集)问题(MOP)中的鲁棒可行集定义为

记(MOP)所有G-真有效解构成的集合为S，且本文所讨论的鲁棒真有效解都指鲁棒G-真有效解.

(3)(SP)λ的鲁棒解集为

那么由定理1有：Sλ⊆S.本文只研究这种特殊的标量化(SP)λ问题的鲁棒解的刻画.

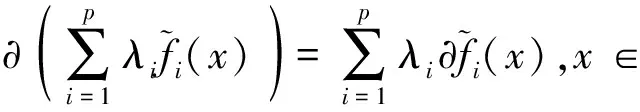
是闭凸集，且

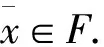
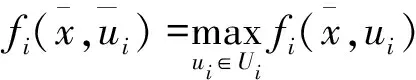
(1)

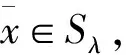
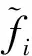
(2)

接下来只需证

F={x：gj(x，vj)≤0，vj∈Vj，j∈J}

那么，把假设运用到拉格朗日对偶[11]，就有：

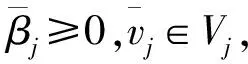
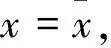
因此，

即证得式(1)成立.

(必要性)成立只需要用到凸规划在凸性条件下的最优性充分论断.

2 主要结果

在这一部分，根据给定问题的一个鲁棒解点得到了各种鲁棒解集的刻画.本文首先得到目标函数的次微分在解集上的基本性质.注意，在没有不确定集的情况下，单目标优化问题的目标函数的次微分在它解集的相对代数内部上是连续的，对于数据不确定型凸优化问题的这个一般结果如下.

其中，

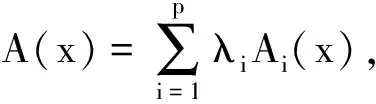
证对任意的x1，x2∈riSλ.鲁棒解集Sλ是如下这个非光滑凸优化问题的解集：

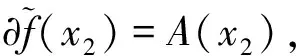
下面证第二个论断，令x∈riSλ，x′∈Sλ.那么，对任意的γ∈(0，1)，γx+(1-γ)x′∈riSλ，令ω∈A(x)，并令γn→0.

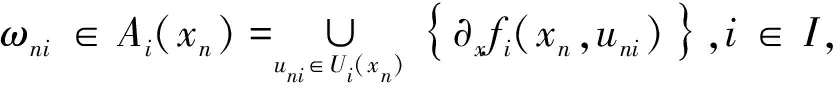
将以上P个不等式分别乘上λi再相加得：

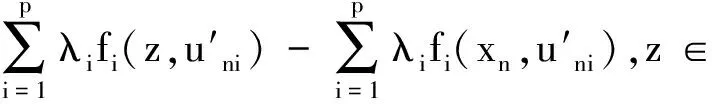
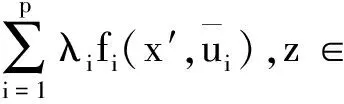
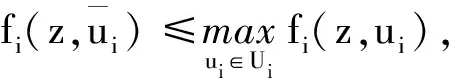
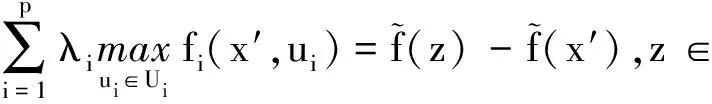
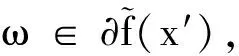
A(x)⊆A(x′)

注1广义常微分性质在没有不确定集的情况下，对于一个光滑凸优化问题也成立，即目标函数在解集上的梯度是常值.

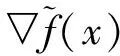
在如下的命题中，本文获得了一个基本的鲁棒解集的刻画.

Sλ={x∈F：<ωa，x-a>=0，

∃ωa∈A(x)∩A(a)}

其中：

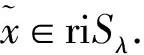
因此有：

(1-γ)<ωi，x-y>=

把以上p个不等式分别乘上λi，i=1，2，…，p再相加得：

又

同样可以得到：

因为γ∈(0，1)，则

<ω，x-y>≤0，<ω，y-x>≤0

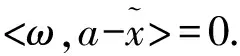
则证得：

∃ω∈A(x)∩A(a)且<ω，x-a>=0

那么就有：

则有：

又a∈Sλ，则x∈Sλ.

注2对数据不确定集是仿射形式的参数化鲁棒最优性问题时fi(x，·)，i∈I的凹性假设是自动成立的.

对问题(SP)λ，令F是鲁棒可行集，令Sλ为鲁棒解集.令a∈Sλ且有

满足

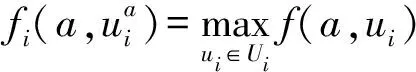
(3)

定义拉格朗日函数La(·，βa，ua，va)为

La(x，βa，ua，va)=

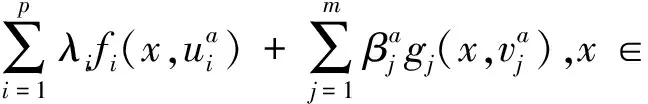
gj(x0，vj)<0，vj∈Vj，j∈J

且La(·，βa，ua，va)在Sλ上是常数.

证由a∈Sλ及命题2则有：

0∈La(a，βa，ua，va)

0≤La(x，βa，ua，va)-La(a，βa，ua，va)

(4)

其中，由一个鲁棒解的乘子刻画可知最后一个等式成立.又由每一个x∈Sλ有：

因此，对每一个x∈Sλ有：

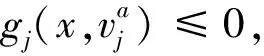
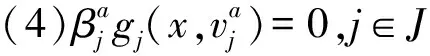
又对每一个x∈Sλ有：

因此：

又对每一个x∈Sλ有：

则La(·，βa，ua，va)在Sλ上是常数.

证[⊆]令x∈Sλ，显然x∈F.由乘子的刻画可知，存在

那么，存在

使得ωa+za=0.则有：

由定理3，x∈Sλ，a∈Sλ，则有：

<ωa，x-a>≥0

(5)

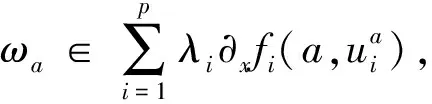
(6)

由式(5)和式(6)，可得到：

<ωa，x-a>=0

(7)

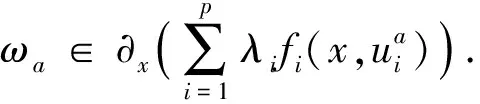
<ωa，y-x>=<ωa，y-a>+

<ωa，a-x>=<ωa，y-a>≤

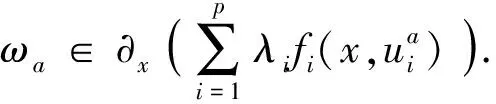
[⊇]令x∈F满足

且存在

使得<ωa，x-a>=0.因此，由

又a∈Sλ且x∈F，则x∈Sλ.

注3 对于不确定光滑凸优化问题的鲁棒解集也有相似的乘子刻画.