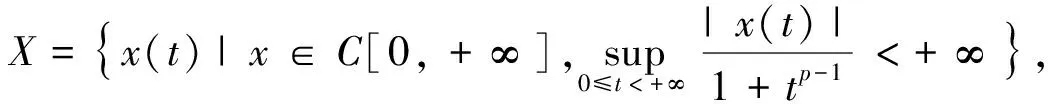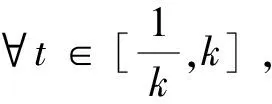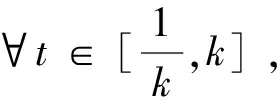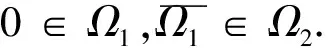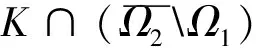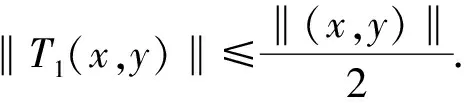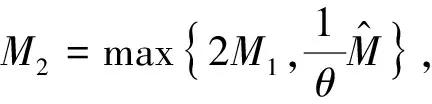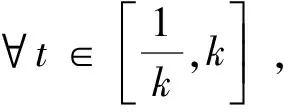无穷区间上分数阶耦合微分系统积分边值问题正解的存在性*
许文序,周宗福
(安徽大学 数学科学学院,合肥 230601)
0 引 言
分数微积分是整数微积分的一种推广.在实际问题中,分数阶模型比整数阶模型更有应用价值.近年来,分数阶微分方程引起了人们极大的关注,除了其自身理论的深入发展,它在分子物理学,流体力学,黏弹性力学,电化学分析,生物系统的电传导等领域有广泛的应用[1-7].大部分学者致力于有限区间上的分数阶边值问题[8-11],对无穷区间上的分数阶耦合微分系统边值问题的研究还相对较少。
文献[12]研究了无穷区间上带有积分条件的分数阶微分方程边值问题:
利用Leggett-Williams不动点定理获得多个正解的存在性。
文献[13]讨论了一类具有耦合积分边界条件的分数阶微分方程问题:
其中u,v>0,α-v≥1,β≥1,通过利用Schauder不动点定理,得到了解的存在结果。
在以上文献的基础上,考虑下面无穷区间上具有积分边界条件的分数阶耦合系统的边值问题:
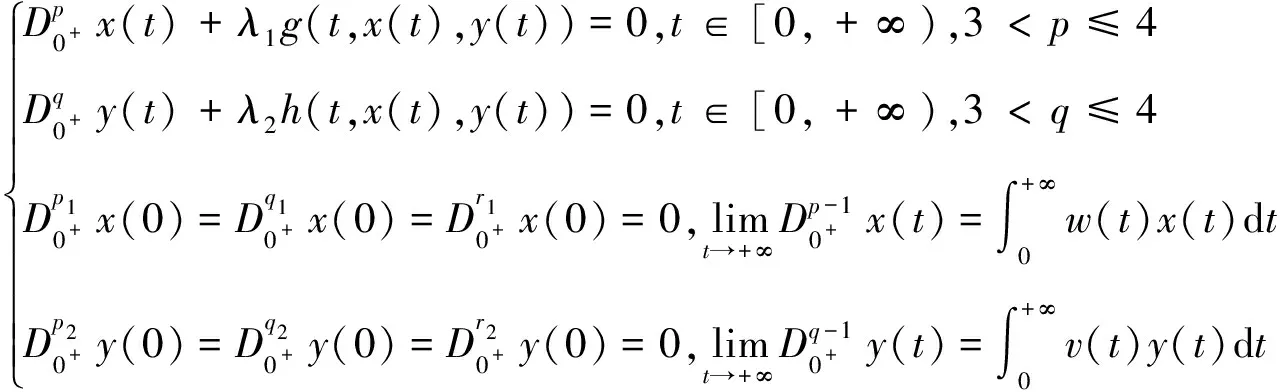
(1)
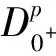
首先给出边值问题(1)相应的带积分条件的耦合线性系统解的表达式,再利用锥上Krasnoselskii不动点定理得到上述耦合系统边值问题(1)正解的存在性。
假设以下条件成立:
(A1)①g,h∈C([0,+∞)×[0,+∞)×
[0,+∞),×[0,+∞));
② λ1,λ2是两个正值参数;
③p1∈(0,p-3),q1∈(0,p-2),r1∈(0,p-1),
p2∈(0,q-3),q2∈(0,q-2),r2∈(0,q-1)
(A2)w,v∈L[0,+∞)w,v非负且
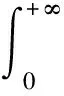
1 预备知识和引理
首先给出一些分数阶微积分的定义和引理。
定义1[2]函数y:[0,+∞)→R的a阶Riemann-Liouville积分定义为
其中式(1)右边在[0,+∞]上是逐点定义的。
定义2[2]函数y:[0,+∞)→R的a阶Riemann-Liouville导数定义为
其中a∈[n-1,n),其式(2)右边在[0,+∞)上是逐点定义的。:
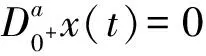
x(t)=c1tα-1+c2tα-2+…+cNtα-N,ci∈R,i=1,2,…,N,其中N是不小于α的最小整数。
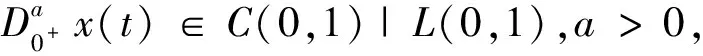
ci∈R,i=1,2,…,N
其中N是不小于a的最小整数。
引理3 设φ∈C([0,+∞],R),3 的解为 这里G(t,s)=G1(t,s)+G2(t,s),且 又有 下面确定c1: (2) 式(2)两边乘上h(t)且从0到+∞积分得: (3) 将式(3)代入式(2)得 证毕。 注1 设ψ∈C([0,+∞],R),3 的解为 这里H(t,s)=H1(t,s)+H2(t,s),且 由引理3及注1可知,边值问题式(1)等价于如下积分系统: 根据求得的格林函数Gi(t,s),Hi(t,s)(i=1,2),易见以下引理成立: 引理4Gi(t,s),Hi(t,s)(i=1,2)在[0,+∞]×[0,+∞]上是连续的,且Gi(t,s)≥0,Hi(t,s)≥0,∀t,s∈[0,+∞],i=1,2. 引理5[14]设k>1,则 考虑乘积空间X×Y,定义其上的范数为((x,y))=(x)+(y).由文献[14]知,(X,(·)),(Y,(·)),(X×Y,(·))是Banach空间. 定义锥 K={(x,y)∈X×Y;x,y≥0, 其中 定义算子T:X×Y→X×Y 易知T的不动点即为边值问题式(1)的解. 引理6T(K)⊂K,T:K→K是全连续算子. 同样,任取(x,y)∈K,令 θ2‖T2(x,y)‖≥θ(‖T1(x,y)‖+‖T2(x,y)‖)= θ‖(T1(x,y),T2(x,y))‖. 可见T(K)⊂K.仿文献[15]中定理3.2的有关可知,T:K→K是全连续的.证毕. (1)‖Tx‖≤‖x‖,x∈K∩∂Ω1且‖Tx‖≥‖x‖,x∈K∩∂Ω2; (2)‖Tx‖≥‖x‖,x∈K∩∂Ω1且‖Tx‖≤‖x‖,x∈K∩∂Ω2; 假设: 定理1 假设(A1),(A2)成立,g0=h0=0并且g∞=+∞或h∞=+∞,则分数阶微分方程(1)至少有一个正解. 证明选取ε0>0,使得 由于g0=h0=0,故对上述ε0,∃M1>0,使得当,0 于是当0≤x(t)+y(t)≤M1时,对∀t∈[0,+∞),有: 作Ω1={(x,y):(x,y)∈X×Y,‖(x,y)‖ 任取(x,y)∈K∩∂Ω1‖(x,y)‖=M1,∀t∈[0,+∞)有: 因此,对取(x,y)∈K∩∂Ω1有: ‖T(x,y)‖=‖(T1(x,y),T2(x,y)‖= ‖T1(x,y)‖+‖T2(x,y)‖≤‖(x,y)‖ (1)若g∞.取β0>0,使得 即∀t∈[0,+∞]有: Ω2={(x,y)∶(x,y)∈X×Y,‖(x,y)‖ 任取(x,y)∈K∩∂Ω2,有 这里的θ即为锥K定义中的θ. ‖(x,y)‖ 可见,‖T1(x,y)‖≥‖(x,y)‖.因此,对(x,y)∈K∩∂Ω2,有 ‖T(x,y)‖=‖(T1(x,y),T2(x,y))‖=‖T1(x,y)‖+‖T2(x,y)‖≥‖(x,y)‖ (2)若h∞=+∞,仿上述分析,类似可作出Ω2.对此,Ω2,∀(x,y)∈K∩∂Ω2,‖T(x,y)‖≥‖(x,y)‖. 根据引理7可知,T存在一个不动点(x,y)∈K∩∂(Ω2|Ω1),M1≤‖(x,y)‖≤M2,此不动点即为边值问题(1)的一个正解.证毕.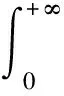
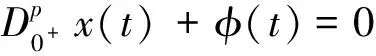

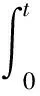


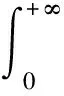

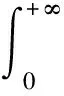
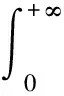
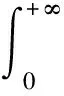
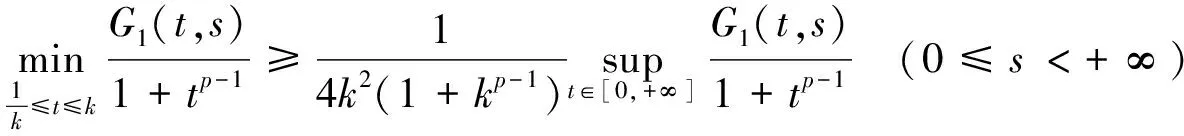
2 边值问题式(1)正解的存在性