一类复平面内二阶微分方程解的渐近式*

崔庆岳，赵国瑞

(广州城建职业学院 人文学院，广州 510925)

0 引 言

考虑下面的积分方程：

(1)

其中积分核k(x，ξ，s)满足下列条件：

① 对于复平面上的某一集合E内的一个固定s和[a，∞)上固定的x，k(x，ξ，s)关于ξ在[a，∞)上是可积的；

④ 函数f(x，s)在a≤x<∞，s∈E上关于x，s是连续的、有界的.

由积分方程理论可知：

引理1若积分方程式(1)中的积分核满足上述条件①—条件③，函数f(x，s)满足条件④，则方程式(1)具有一个在x∈[a，∞)和s∈E上连续有界的解u(x，s).

证明通过迭代的方法逼近方程的解，假定

u0(x，s)=0

(2)

其中a≤x<∞，s∈E.

记ε0={(x，s)，x∈[a，∞)，s∈E}，下证un+1(x，s)在ε0上连续有界，并且对∀(x，s)∈ε0积分方程式(2)收敛.

当n=0，上述结论显然成立；当n=m时，假设上述结论成立.

当n=m+1时，对∀(x，s)∈ε0，|um(x，s)|≤cm，则

成立.从而证明了积分方程式(2)的收敛性和um+1(x)的有界性.

对于(x0，s0)∈ε0，有

|um+1(x，s)-um+1(x0，s0)|=

(3)

取N充分大，令(x，s)无限接近(x0，s0)，由k(x0，ξ，s0)的性质及um(ξ，s)的连续性可得式(3)右端可以充分小，所以um+1(ξ，s)在ε0上连续.

下面考虑级数:

u0(x，s)+[u1(x，s)-u0(x，s)]+

[u2(x，s)-u1(x，s)]+…+[un(x，s)-un-1(x，s)]+

[un+1(x，s)-un(x，s)]+…

(4)

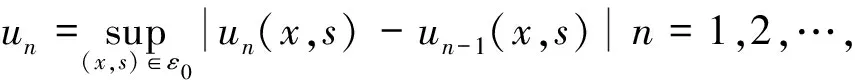
|un+1(x，s)-un(x，s)|=

即un+1≤unγ.

又由于γ<1，所以级数u0+u1+u2+…+un+…收敛，从而级数式(4)在ε0上一致收敛，并且

所以u(x，s)是积分方程式(1)的解，而且根据um(x，s)的性质以及在ε0上的一致收敛性可知，u(x，s)在ε0上连续，有界.

引理2若积分方程式(1)的积分核k(x，ξ，s)同时满足条件①—条件④，并且有条件：

⑤E是复平面C上的开集；

⑥ 对每个固定的x∈[a，∞)，f(x，s)在E上是解析函数；

事实上，对每个固定的x∈[a，∞)，un(x，s)在E上是解析函数，由一致收敛性得u(x，s)在E上也是解析函数.

(5)

满足条件①—条件③.

注2若φ1(x，ξ，s)，φ2(x，ξ，s)对固定的x，ξ∈[a，b]关于s在E上解析，则k(x，ξ，s)满足条件⑦.

在实数域内微分算子已有大量的成果，包括自伴域、谱理论等方面已有较系统和完善的结论，其中关于特征值和方程解的研究也有大量的成果，譬如在文献[1]中作者利用E.C.Titc-hmarsh所引进的函数论的方法得到Sturm-Liouville问题存在可数个实的单重特征值，并且给出特征值及特征函数的渐近式；在文献[2]中作者给出了带有独立参数的特征值和特征函数的渐近式；在文献[3-4]中作者给出了在满足不同条件下的谱函数的渐近式；文献[5-6]分别给出了线性和非线性二阶微分方程解的渐近式，得到了比较好的近似结果；文献[7]中则给出了一类二阶微分方程解的渐近性的证明方法；文献[8]利用通解的结构和自由项的形式来求二阶常系数线性齐次微分方程的解；文献[9]则利用微积分运算把一个二阶微分方程的边值问题转化为积分方程，然后用泰勒矩阵的方法得到其近似解.

以上结论都是基于实数域内得出的，但是在复数域内的研究成果还相对较少，在文献[10]中作者给出了复平面内复值函数q(x)在满足分段连续和绝对连续条件下方程解的渐近式；文献[11]中作者在复平面内给出了带有复数系数的Emden-Fowler型方程解的渐近性.

1 微分方程l(y)=λy的解系

主要研究二阶微分方程：

l(y)=-y″+q(x)y(0≤x≤∞)

生成的微分算子的相关结论，其中q(x)为[0，∞)上的复值函数，且在[0，∞)上可积.

下面考虑微分方程：

l(y)=λy

(6)

方程式(6)可化为

y″+λy=q(x)y

(7)

利用常数变易法可得方程式(7)的解：

y(x，s)=c1eisx+c2e-isx+

其中微分方程的特征根λ满足条件：

① 若令c1=1，c2=0，x1=x2=∞，得到方程式(7)的特解：

eis(ξ-x)]q(ξ)y(ξ，s)dξ

(8)

根据积分方程理论可知，当x充分大时，式(8)有解.

设y(x，s)=eisxz(x，s)，则方程

有一个非零解z(x，s)

下面考虑积分核k(x，ξ，s)为如下形式：

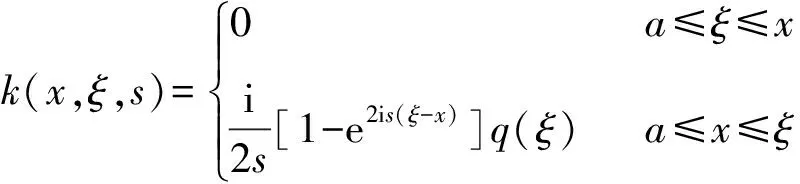
的积分方程式(1)，即在式(5)中，有

设E是复平面C上的集合，|s|≥γ>0，s∈C，τ≥0，则对ξ>x，且s∈E，有

|e2is(ξ-x)|=e-2τ(ξ-x)≤1

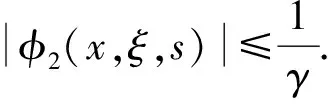
y(x，s)=eisxz(x，s)

(9)

是积分方程式(8)的解，也是方程式(6)的一个满足一定初始条件的特解.

定理1方程式(6)存在一个解y1(x，s)满足积分方程：

② 若令c1=0，c2=1，x1=x2=∞，同样得到方程式(6)的另外一个特解.

定理2 方程式(6)存在一个特解y2(x，s)满足积分方程

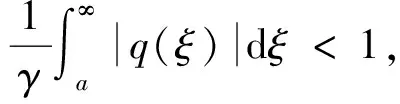
2 微分方程l(y)=λy解的渐近式

① 考虑微分方程l(y)=λy的解y1(x，s)，y2(x，s)及其导数在x→+∞时的渐近式，其中s=σ+iτ，0≤args<π，τ≥0.

y1(x，s)=eisx[1+o(1)]

且在区域|s|≥γ>0，τ≥0上关于s一致成立.

证明考虑积分方程：

对充分大γ，当|s|≥γ>0，x≥a时，由定理1可知z(x，s)在上述区域内有界，不妨设|z(x，s)|≤c1，0≤x≤∞，|s|≥γ，则当|s|≥γ>0，x≥a时，

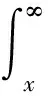
在区域γ≤s<∞，γ>0内关于s一致成立.

证明同定理3.

② 考虑微分方程l(y)=λy的解y1(x，s)，y2(x，s)及其导数在s→+∞时的渐近式，其中s=σ+iτ，0≤args<π，τ≥0.

定理5 对于复数虚部τ≥0，且当s→+∞时，

e-isxo(s-1)

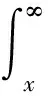
证明对y1(x，s)进行迭代可得：

eis(η-ξ)]q(η)eisηdηdξ+eisxo(s-3)

(10)

对式(10)右端第二项估计可得:

(11)

其中式(11)第二项取绝对值，再由定理1可得：

同样根据定理1，对式(10)第三项进行估计可得：

综合以上可得定理5成立.

利用相同的方法对函数y2(x，s)及其导数

定理6 对于复数虚部τ≥0，且当s→+∞时，

证明同定理5.

通过以上证明，给出了微分方程在满足不同初始条件下的两个特解及其导数在两种不同变化趋势下的渐近式，并且渐近式的精度取决于复平面内所选定的区域；另外，在s→+∞的变化趋势下，方程解的近似精度主要取决于函数q(x)的性质，如果函数q(x)∈[0，+∞)除了满足绝对连续，q′(x)存在且可积之外，还存在高阶导数，则二阶微分方程特解的渐近式将会更加精确，这是本文后续要研究的内容.