特征级融合方法及其在医学图像方面的应用

张飞飞 周 涛,* 陆惠玲 梁蒙蒙 杨 健

1(宁夏医科大学公共卫生与管理学院 宁夏 银川 750000) 2(宁夏医科大学理学院 宁夏 银川 750000)

0 引 言

图像融合按照不同的层次划分为像素级融合、特征级融合和决策级融合，其中特征级融合属于中间层次的融合。首先对原图像进行归一化、几何变化等预处理，其次根据不同模态图像的特点提取特征构造原始特征空间，最后对特征信息进行综合处理。其目的是实现不同模态图像的分类、汇集和综合。

特征级融合方法主要包括特征变换和特征选择两种，特征变换是将数据从原始特征空间映射到较低维数的特征空间中，降低数据特征空间的维数、消除特征相互之间的相关性，减少冗余和不相关的特征[1]。特征选择是从原始特征空间中选择出一定数量的具有代表性的特征，达到降低数据集维度的目的，包括特征子集的生成、评价特征子集、停止准则的判断、验证方法四个步骤。图像特征级融合作为信息融合的重要分支，广泛应用于临床医疗诊断、遥感技术、计算机视觉以及军事检测等领域。其中在医学图像处理领域主要应用于计算机辅助诊断，减轻临床医生的工作负担，减少漏诊和误诊。如Zhu等[2]将特征不对称度量纳入目标函数的正则化项，提出减少超声图像斑点的优化方法，有效区分特征和斑点噪声，有助于超声在临床诊断和治疗中的应用；任亚平[3]提出核独立成分分析用于医学图像去噪，可以保留图像细节信息提高图像质量，降低计算复杂度；Li等[4]提出了一种基于监督正交线性局部切线空间排列算法和最优监督模糊C均值聚类算法，用于生命等级的识别，提高了模式识别效率，避免了局部最小化。

虽然特征级融合方法应用广泛，但其基础理论和结构体系还不完整，技术划分不是很明确。特征级融合的主要问题是提取何种特征构造原始特征空间以及如何获取分类性能较好的特征子集，即特征的变换和选择，同时面向具体的应用时，选取何种融合算法也是应该考虑的重要因素。因此，本文从特征变换和特征选择两个维度对特征级融合方法进行分类总结，从理论层面对改进的方法进行汇总，并简单介绍其在医学图像处理领域的应用。

1 图像特征级融合流程

图像特征级融合分为图像获取、预处理、提取特征构造原始特征空间、通过特征变换或特征选择进行特征融合达到降低维度的目的，最后进行决策识别。随着计算机技术的发展，学者们根据实际情况提出了很多特征级融合方法，分为特征变换和特征选择。特征变换是将原始特征空间映射到低维空间中[1]，减少特征空间维数，减少相关性或冗余性较强的特征，压缩数据量和结构，特征变换方法按照是否线性可分分为线性和非线性两大类。特征选择是从原始特征空间中选择最有代表性的特征以降低数据集维度，包括候选特征子集的生成、子集评价、停止准则、验证方法四个步骤。如图1所示，以医学图像为例，给出了特征级融合流程图。

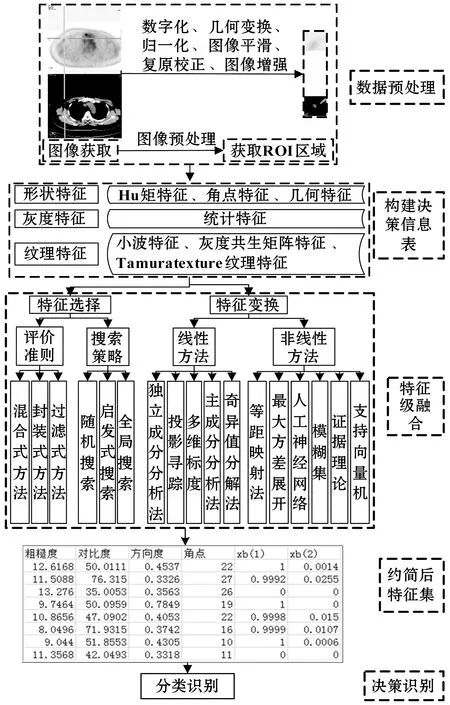
图1 图像特征级融合流程图(以医学图像为例)

2 特征变换方法及在医学图像中的应用

在图像处理领域，专家学者们根据实际应用提出了很多特征变换算法，本节对特征变换算法及其在医学图像中的应用进行梳理总结，按照是否线性可分(线性方法和非线性方法)和是否有监督(监督学习、半监督学习和无监督学习)两个维度进行分类总结，归纳其发展现状和方向。线性方法和非线性方法具有各自独特的优势，应根据所需处理的数据特点，选择合适的方法。

2.1 线性方法

线性特征变换方法是数据降维算法的一个重要分支，是一种比较简单、成熟的降维方法。该方法要求数据集满足全局线性结构并且各变量之间保持独立无关联。线性方法的核心是采用线性变换的方式从高维数据中提取最能够体现样本差异的成分，得到的数据特征能够尽可能反映原始高维样本数据的特征。图2为线性特征变换算法分类图，在医学图像特征级融合领域，专家学者提出了很多线性特征变换方法，如判别分析法[5]、多维尺度法[6]、Fisher鉴别分析[7]、K邻近法[8]、朴素贝叶斯算法[9]、主成分分析法[10]、半监督鉴别分析法[11]、保持投影法[12]、独立成分分析法[13]、局部特征分析法[14]、典型相关分析法[15]等，这些方法在很多文献中都进行了总结阐述，下面重点介绍奇异值分解法和非负矩阵分解法及其改进算法，介绍其在特征级融合过程中的应用现状、分析优缺点，并阐述其发展方向。

图2 线性特征变换方法分类图

2.1.1 奇异值分解

奇异值分解SVD(Singular Value Decomposition)方法是1873年由Beltrami首次提出的，是一种有效的代数特征变换方法，具有稳定性、比例和旋转不变性等性质，在医学图像处理领域的应用包括图像增强、压缩、复原、降噪等。如Chen等[16]提出了一种对称SVD表示方法，并将其应用于人脸识别；Zhang等[17]提出一种高阶SVD方法，用于磁共振图像中噪声的消除，该方法显著减少了条纹伪影，提高了降噪质量；Tai等[18]提出了一种用于面部识别的学习判别SVD方法，该方法在处理照明、遮挡、伪影等方面具有良好的效果；Chen等[19]提出了一种广度截断SVD方法，与现有的时域法相比具有更高的精度、适应性和抗躁等优点。虽然SVD具有全局意义上的数据处理能力，但仍存在不足，如算法的可解释性不强，对噪声数据的处理能力不稳定等。特别是当处理数据是高维海量时，SVD分解的速度和精度会成为其发展的瓶颈。

2.1.2 非负矩阵分解

非负矩阵分解NMF(Non-negative matrix factorization)是1999年D.D.Lee和H.S.Seung首次提出的，其应用前提是矩阵中的元素均为非负数据，具有实现简单方便，存储空间占用少的特点，在实际生活中的应用越来越广泛，如图像处理、语音分析、文本分析、数据挖掘、模式识别等。很多专家学者在经典NMF的基础上提出了很多改进算法，主要分为约束NMF、结构化NMF和泛化NMF三种。如杨永生等[20]提出利用多核NMF对原始数据进行约简，多核SVM进行分类识别，实验证明该方法可有效降低原始数据的维数，提高分类识别的效率；Gao等[21]提出了一种空间加权NMF，并结合分层交替最小二乘法用于图像、视频等视觉信号的处理；Shu等[22]提出了一种无参数自动加权多重图形正则化NMF，证明其具有良好的性能。目前，NMF的主要问题是容易早熟收敛、收敛速度慢，后续研究一方面要解决收敛速度和唯一解问题，另一方面也要拓宽NMF在实际中的应用。

2.2 非线性方法

虽然线性特征变换方法简单易于实现，但是现实中大多数数据具有“高维数、非结构化”的特点，此时传统的线性特征变换方法就不能得到期望的约简效果。因此，近年来许多非线性特征变换方法在理论和应用层面都得到了很大的发展，如核Fisher鉴别分析[23]、拉普拉斯特征映射[24]、随机领域嵌入[25]、核独立成分分析[26]、局部线性嵌入[27]、等距映射[28]、核主成分分析[29]、局部切空间排列[4]、最大方差展开[30]、证据理论[31]等。图3为非线性特征变换算法分类图，其中，神经网络、模糊集、支持向量机应用最为广泛，因此对这三种方法及其改进算法进行梳理总结。

图3 非线性特征变换方法分类图

2.2.1 人工神经网络

人工神经网络ANN(Artificial neural network)是对人脑神经元网络的一种抽象表达，由大量处理单元按照不同的方式互联组成，对于处理含糊性和不确定性的图像问题具有很好的效果。随着逐渐深入的研究，ANN的应用已经越来越广泛，如模式识别、卫生保健、生物医学等。目前，已有大约40种ANN模型，如Kohonen神经网络、Elman动态神经网络、自组织映射神经网络、脉冲耦合神经网络等。ANN在疾病诊断过程中的应用广泛，如文献[32]使用卷积神经网络对黑色素瘤进行早期诊断，诊断精度高于其他算法；文献[33]等采用误差反向传播算法，从输入数据中提取有价值的体积和检测肺结节CT图像子块来构建检测胸部CT图像中肺结节的CADe系统；文献[34]提出反向传播神经网络，用于超声图像去噪和去模糊处理；文献[35]使用神经网络对计算机断层扫描图像进行去噪处理。为提高ANN算法的效率及其鲁棒性，与其他方法如模糊系统、遗传算法、进化机制、混沌理论、小波算法、粗集理论等相结合是其研究的重要方向，同时改进网络的拓扑结构、权重、激励函数及学习规则也是发展的一个方向。

图4为人工神经网络方法分类图。

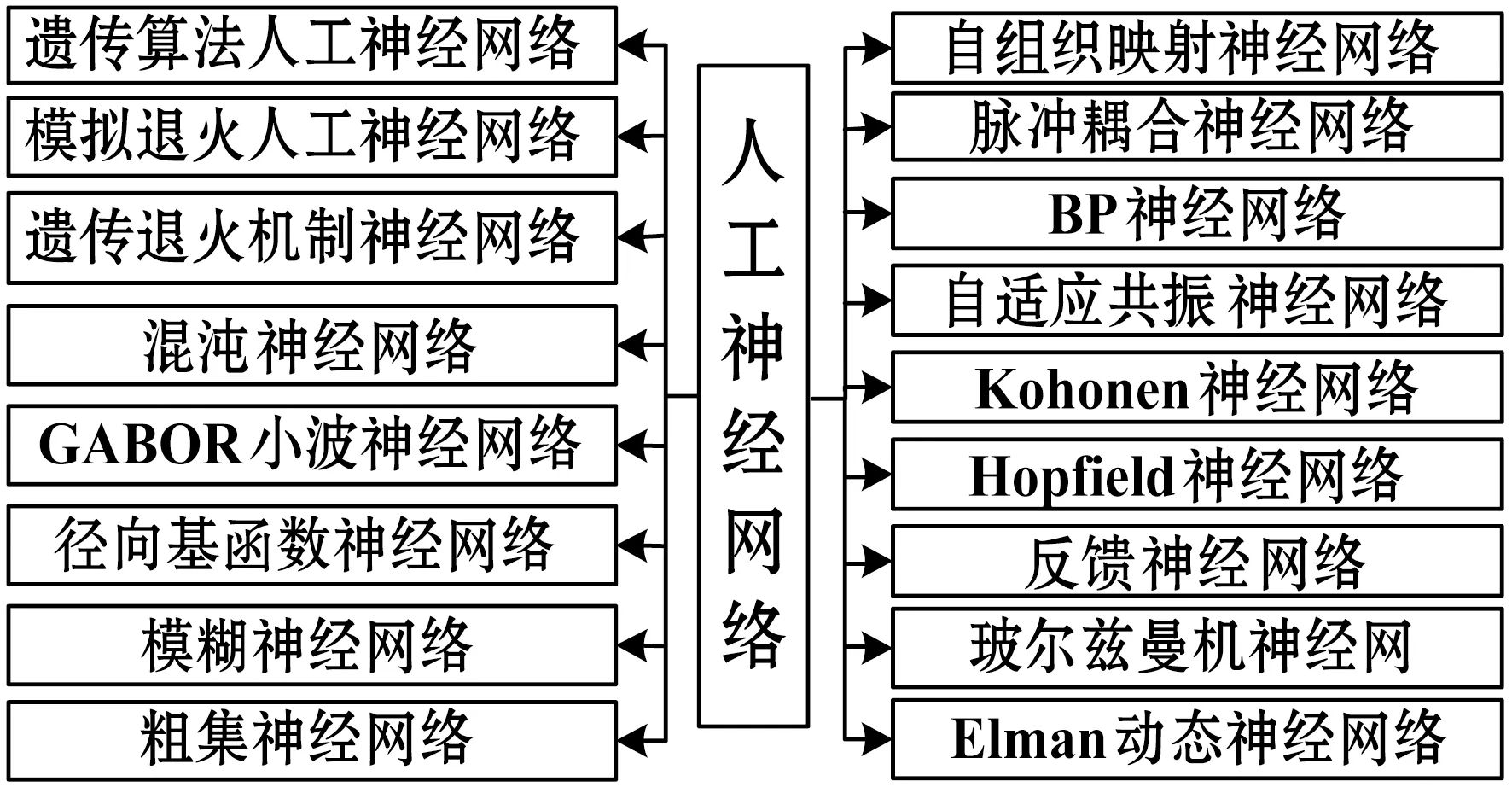
图4 人工神经网络方法分类图

2.2.2 支持向量机

支持向量机SVM(Support vector machine)于1995年被Corinna Cortes和Vapnik等首次提出，该模型的基础是统计学习和结构风险最小原理。SVM具有泛化能力强、样本维数大小不敏感、全局收敛等特点，在理论和应用方面都取得飞速发展。目前在理论方面：SVM的理论改进主要包括四个方面：一是SVM本身的改进，包括光滑SVM、拉格朗日SVM、最小二乘SVM、Robust SVM、单类SVM、小波SVM等；二是核函数的选择，常用的核函数包括多项式核函数、线性核函数、Sigmoid核函数和径向基核函数[36]；三是参数的优化，群智能算法经常被用来优化SVM的惩罚因子和核函数参数，例如蝙蝠算法、萤火虫算法、人工蜂群算法、果蝇算法、蚁群算法、灰狼算法、人工鱼群算法等[37]；四是与其他分类算法的结合使用，包括AdaBoost、K临近、隐马尔科夫等。在医学图像处理领域的应用如文献[38]使用SVM进行阿尔茨海默病、轻度认知障碍和正常人的分类，明显提高了精度和性能；文献[39]使用SVM在肺癌早期诊断的CAD系统中进行特征分类；文献[40]使用SVM进行乳腺癌的筛查，提高了敏感性、特异性和准确性。虽然SVM的理论研究和应用已经成为数据挖掘的热点，但仍存在一定的缺点，如当数量较大时，计算速度大幅度减慢，对噪声和孤立点数据非常敏感。拓宽待解决问题的应用领域、与其他机器学习方法进行融合、加强训练算法等是今后研究的重要方向。对SVM改进算法分类如图5所示。

图5 支持向量机改进算法分类图

2.2.3 模糊集

模糊集(Fuzzy set)理论是L.A.Zadeh在1965年提出的，主要思想是用属于的程度大小来描述属性之间的属于或者不属于关系，表达差异的一种中间过度，是用精确性去逼近模糊性，已经成为处理不确定信息和知识的重要数学工具。近年来，模糊集在图像增强、滤波、边缘检测等领域不断扩展，在提高信噪比、保留细节信息等方面具有很大的优越性。为了提高系统在处理不确定性信息方面的能力，对模糊集进行不断扩展，提出很多改进模型，如n维模糊集、双极值模糊集、直觉模糊集、Flou模糊集、模糊值模糊集、区间值模糊集、扰动模糊集、粗糙模糊集、犹豫模糊集等。在医学领域的应用广泛，例如Liang等[41]在决策粗糙集理论的基础上提出了对偶犹豫模糊集，通过紧急血液转运评估来验证该模型的有效性；文献[42]提出一种新的确定直觉模糊集距离度量的方法，用于提高医学图像诊断的正确性，在真实的数据集上验证了该方法的适用性和有效性。目前，完善模糊集理论、改进经典算法、与其他优化方法相结合是其发展的主要方向。如图6为模糊集及其改进方法分类图。

图6 模糊集改进方法分类

3 特征选择方法及在医学图像中的应用

特征选择也称候选特征子集的选择，是指从原始特征数据中选择分类性能较好的特征子集，使选择后的特征构建的模型效果更好。文献[1]中根据选择思想不同分为特征优选和特征劣选。特征优选是指从原始特征空间中选出分类性能较好的特征子集，特征劣选是指从原始特征中剔除冗余或无关的特征子集。特征选择分为特征子集的生成、评价特征子集、判断停止准则、验证方法四个部分。

3.1 特征子集的生成

特征选择的关键步骤就是生成候选特征子集，特征子集生成方式取决于不同的搜索策略，主要分为全局最优搜索策略、随机搜索策略、启发式搜索策略和混合搜索策略四类。下面按照四种搜索策略对基本的特征选择算法进行分类总结，主要方法分类如图7所示。

图7 按搜索策略划分特征选择算法

3.1.1 采用全局最优搜索策略特征选择算法

全局最优搜索是一种通过算法的不断迭代来实现的穷举式搜索，可以搜索到所有符合条件的特征子集。常用的全局最优搜索方法包括：广度优先搜索、分支界限搜索、定向搜索和最优优先搜索等。其中广度优先搜索又名宽度优先搜索，时间复杂度高，实用性低；定向搜索相比宽搜可以节省时间和空间，可以算是启发式搜索的一种；最优优先方法的搜索过程是计算特征集合评价函数，再将计算结果进行排序，选择代价最小的路径继续搜索。由于在搜索过程中总是放弃代价大的路径，因此最终得到的特征子集就是搜索过程中代价最小的问题答案。分支界限搜索是使用最广泛的一种全局最优搜索算法，通过剪枝处理来减少搜索时间，具体原理是将需要解决的原始问题逐步分解成为多个不能再分解的子问题，通过求解子问题的最优解得到原始问题的最优解，它的优点是在保证特征数目一定的情况下，搜索到相对而言的最优特征子集。

虽然全局最优搜索策略划分的方法能找到全局最优解，但随着特征数量的增大，计算时间和空间大幅增加，因此无法广泛应用。

3.1.2 采用随机搜索策略的特征选择算法

随机搜索策略的特征选择算法首先随机产生一个候选特征子集，再根据实际问题的启发信息逐步搜索全局最优解。常用的方法包括遗传算法、粒子群算法、免疫算法、禁忌搜索算法、粗糙集、差分进化等。遗传算法和粗糙集的应用非常广泛，下面对这两种方法进行归纳总结。

(1) 粗糙集。粗糙集RS(rough set)是处理模糊性和不确定性信息的一种数学工具，是一种新的软计算方法，因其无需先验知识的特性，在机器学习、分析决策、过程控制等领域引起了专家学者的广泛关注，在传统Pawlak RS的基础上相继提出了很多改进算法，例如粒度RS、邻域RS、加权RS、覆盖RS、灰色RS、决策RS、模糊RS、优势RS等。其中模糊RS的应用最为广泛，与其他方法相结合，形成一系列的改进模糊RS，例如多粒度模糊RS、F-模糊RS、直觉模糊RS、双论域模糊RS、稳健模糊RS、模糊决策RS等。在医学图像处理领域，RS广泛应用于图像滤波、识别、分类、融合、分割；医学数据挖掘；疾病预测、医疗诊断、疾病分类等。例如Wang等[43]提出首先使用ANN对乳腺癌数据进行离散化，GA进行属性约简，最后使用RS从决策表中归纳诊断规则，相比传统的CAD系统，诊断精度显著提高；Guo等[44]提出了一种基于模糊RS的特征选择方法，用于乳腺癌的风险评估，提高了降维效率和分类准确率；文献[45]提出了直觉模糊RS模型，用直方图作为RS的下近似，直觉模糊直方图作为上近似进行脑MR图像的分割，定量评价表明，该算法具有一定的优越性。虽然RS无需先验知识，但缺乏处理数据本身模糊性的能力，且对边界区域刻画过于简单，与很多实际问题不符，后续应在这些方面进行改进。图8为粗糙集方法分类图。

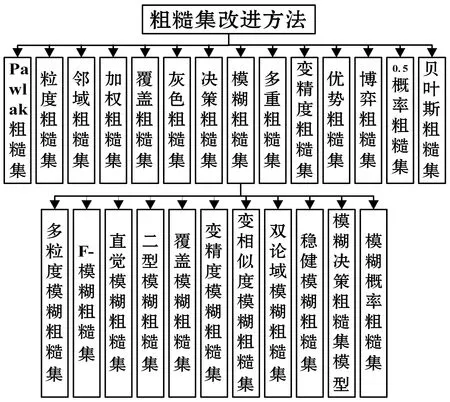
图8 粗糙集改进方法分类图

(2) 遗传算法。遗传算法GA(Genetic Algorithm)是根据生物遗传的规律，通过选择、交叉、变异等遗传操作达到提高个体适应性的目的。虽然GA在机器学习、图形图像处理、社会科学、数据挖掘、人工生命等领域取得了卓越的成效，但是仍然存在收敛速度过快和容易陷入局部最小(早熟)的问题。因此，很多专家学者针对这两个问题在理论层面提出了很多改进算法。例如，为了保持种群的多样性，于歆杰等[46]提出了拥挤GA，根据竞争方式和评价个体生存能力的不同，派生出不同类型的拥挤GA，如：限制性锦标选择方法、多小生境拥挤算法和确定性拥挤算法；王聪等[47]对小生境GA进行改进，提出一种新的混合GA，通过实验证明该算法具有较好的收敛性和较低的时间复杂度。适应度函数改进方面，陈果等[48]提出四种新的GA特征选择适应度函数，即基于改进的距离判据适应度函数、基于平均值方差比的适应度函数、基于Fisher准则的适应度函数和基于最近邻分类法的适应度函数，通过实验证明不同适应度函数的适用性和有效性；李乃成等[49]为了自适应调整变异概率，提出一种具有对偶适应度函数的GA，通过在不同的函数上测试，证明该方法具有较好的收敛速度；杨水清等[50]将乘幂变换和线性尺度变换相结合，提出了一种基于乘幂变换的非线性动态适应度函数，在常用的测试函数上验证算法的有效性与可行性。在遗传算子方面，杨新武等[51]采用自适应比例选择策略，调整平衡算法求精和求泛能力，实验证明该算法可有效克服早熟；李书全等[52]针对不同的编码方式总结了常用交叉算子，并从不同的角度提出了相应的改进算法。同时，也逐步形成了很多混合GA，例如：文化GA、蚁群GA、粒子群GA、模拟退火GA等。GA算法广泛应用于医学图像处理领域，例如文献[53]在混合医学图像检索系统的设计时，采用GA进行特征降维，在保证正确率的前提下降低时间复杂度，解决维数灾难问题；文献[54]提出一种基于改进GA和耦合映像格的混合模型，用于医学图像的加密，实验证明该算法不仅能完成加密工作，也能抵御各种典型的攻击。GA以后研究重点应该是与优化技术的融合，对算法本身的改进以及新算法的提出，更重要的应该是混合GA的研究。GA是对自然进化规则的一个理论性简化，缺乏系统的数学基础，后续应该不断完善基础理论，拓宽应用的范围。从编码、初始种群构建、适应度函数、遗传算子还有混合算法几个方面对GA进行总结，如图9所示。

图9 遗传算法改进方法分类图

随机搜索策略特征选择算法可以获得一个近似最优解，但是，随着特征维数的增加，时间复杂度也会严重增加。

3.1.3 采用启发式搜索策略的特征选择算法

为了避免穷举式搜索带来的计算代价，启发式搜索特征选择算法为了有效指导搜索的方向，在搜索过程中加入了与实际问题有关的启发式信息，以便加速获得优化特征子集的过程。比较典型的搜索算法包括单独最优特征组合、序列前向选择、序列后向选择、增L去R选择、决策树、Tabu搜索以及浮动搜索等。

3.1.4 采用混合搜索策略的特征选择算法

综合上述三种策略优点的混合式搜索策略是今后特征子集产生的新研究方向，可以有效避免单独一种搜索策略的缺点，得到一些在各方面比单独策略更优的特征选择方法。每种搜索策略划分的算法各有优缺点，在处理实际问题时，必须综合考虑问题的时间复杂度、空间复杂度和全局最优解，在这些条件之间寻找一个最佳平衡点。例如当原始特征集合维数较少时，可选用全局最优搜索策略方法；若要求时间复杂度低，对选择的子集全局性要求不高时，可选用启发式策略方法；若需相对较高性能的特征子集，计算时间要求较低时，可采用随机搜索策略方法[55]。

3.2 特征子集评价函数

评价函数是特征子集优劣的判断依据，按特征子集评价标准和算法划分结果如图10所示。

图10 按特征集合评价策略划分图

3.2.1 过滤式评价策略的特征选择方法

Filter过滤式特征选择方法使用评价准则来加强不同的特征与其所属类之间的相关性，达到减弱特征关联性的目的。通常使用的评价准则包括：距离(欧式距离、马氏距离、平方距离等)、信息(信息增益、互信息、最小描述长度等)、依赖度和一致度等。ReliefF系列算法是最常用的Filter特征选择算法。它不依赖于确定的学习算法，而是根据数据集内在的固有特征来评价不同特征的分类性能，找到最优的特征子集，主要通过统计学习的方法检测变量之间的差异性。Filter算法运算的优点是速度较快，但是评价结果与后续学习算法本身的性能之间存在较大偏差。

3.2.2 封装式评价策略的特征选择方法

Wrapper模型是一种有监督学习方法，直接使用分类性能的优劣作为评价特征重要性程度的标准，它的最终目的是构造分类器模型。因此如果在构造初始分类器的过程中，直接使用分类性能较高的特征，就可以使得分类器模型取得比较高的性能。Wrapper方法决定特征子集优劣的标准是通过在特征选择流程中嵌入其他的学习算法，测试不同算法中特征子集的分类性能来实现的，而很少去关注特征子集中单个特征预测性能的优劣。常用的Wrapper特征选择算法包括基于分类结果矩阵和基于互补系数的方法。Wrapper方法使用后续嵌入学习算法的分类精确度来评价特征子集的优劣，分类的偏差小，但是计算量大，适合于数据量较小的样本，通用性较弱。

3.2.3 Filter和Wrapper组合式算法

Filter结果与最终使用的分类器无关，不便于进一步优化分类器的性能。Wrappe虽然能获得较高的分类率，但不能标记出选择的属性与对象之间的相关性，因此，将Filter和Wrapper两种互补的模式相结合将是未来研究的方向。如：陈岩等[56]利用Filter-Wrapper结合的方法获取特征变量的属性，首先使用Filter方法从原始特征集合中选出一定数量的具有代表意义的特征子集，降低搜索空间的维数。其次使用Wrapper方法从特征子集中二次选出满足精确度要求的特征变量，实验证明该方法的优越性。

3.3 停止条件

特征子集评价完成后要判断是否符合“停止条件”的要求，如果不满足设置的停止条件，搜索过程将进入死循环，无限执行下去。通常选用的停止条件包括：算法运行时间、评价的阈值次数、特征子集的数量、评价函数的阈值以及算法早熟或收敛等。

3.4 结果验证

验证特征子集的优劣一般选用人工或真实的数据集，将经过特征级融合后的约简结果作为分类器的输入进行训练和测试，最后将分类结果与没有经过特征级融合的原始数据集进行比较。比较指标包括分类的时间、空间复杂度以及分类器的精确度等。

特征选择是特征降维方法中非常重要的分支，随着研究逐渐深入，已经形成了很多成熟的方法，但是，研究过程中同样也存在很多问题。例如：如何针对不同数据量、不同数据类型设计最适合的特征选择方法，不同类别特征选择算法之间的相互融合，算法的进一步优化与实际应用等。将来的研究应该在克服这些问题的基础上继续探索，完善特征选择算法体系，为特征降维提供良好的技术支撑。

4 结 语

随着数字图像处理技术的不断发展，相继提出了很多新的方法和技术。本文围绕特征级融合方法，对特征变换和特征选择方法进行了分类总结，通过总结不同方法的发展现状，发现特征级融合仍存在以下不足和需要继续改善的地方：

(1) 虽然特征级融合方法已经提出了很多理论和算法，但未形成一个完善的理论体系，在不同的应用中效果仍然无法系统地评价，因此制定一个比较完善并且客观的评价标准势在必行。

(2) 特征级融合过程中最重要的过程就是特征的提取，当特征数量增加时，融合算法的时间复杂度和空间复杂度会迅速增加，会出现维数灾难问题，因此优化算法降低复杂度是今后发展的重要方向。

(3) 尽管特征级融合研究目前已经有不少的研究成果，但与现实要求还存在很大的差距，很多融合算法的运行速度、精确度、实用性以及鲁棒性等仍需改进。

(4) 特征级融合技术在实际应用中扮演着越来越重要的角色，提取何种特征以及选择合适的融合算法等仍是主要的研究问题。

(5) 医学图像模态众多，功能各异，图像所表现的信息也各不相同，如何针对不同模态的医学图像进行特征变换和选择，从而促进计算机辅助诊断的发展也是今后发展的重要方向。

总之，特征级融合相比像素融合和决策级融合有其独特的优势，在现实中的应用也越来越广泛，为信息处理带来重大的变革，发挥着不可替代的作用。