基于WebGL的三维GIS空间算法的研究与实现

王星捷 卫守林

1(核工业西南物理研究院 四川 成都 610041) 2(成都理工大学工程技术学院 四川 乐山 614007) 3(昆明理工大学信息工程与自动化学院 云南 昆明 650093)

0 引 言

当前多数的Web端的GIS平台主要以二维的为主，许多成熟的三维GIS平台，都已经开发成产品，不仅加载Web三维场景地图大多需要下载额外的插件来实现，而且需要昂贵的平台使用费用。WebGL技术[1]可以直接利用硬件来渲染三维场景，不用下载额外的插件。现在虽然有许多关于利用WebGL技术来渲染[2]三维GIS场景的研究论文，但实现效果不太理想，大多只提供场景模型加载功能，没有具体的二维地图矢量数据的支撑，不能进行空间分析。而且只能实现单一的三维场景[3]，不能实现与二维数据的联动等多方面的空间功能。

目前浏览器对WebGL提供支持，在未来WebGL与地理信息服务技术相结合是发展的趋势。本文基于Web Graphics Library(WebGL)结合Geographic Informatica Service(地理信息服务)对三维数字城市技术进行了深入研究，设计了一套基于WebGL开发三维GIS的技术[4]，充分利用了WebGL与ArcGIS Server的结合，方便地实现了三维编辑、三维查询[5]和三维分析等功能。由于三维模型[6]和三维场景的复杂性[7]，在实现的过程中出现了一些问题：(1) 系统在平移和旋转时，二维空间数据处理和三维模型的显示发生了位移，没有保持空间信息的同步；(2) 实现路径分析数据三维体现时，轨迹显示效果差；(3) 在实现二、三维视图切换，鹰眼滑动，三维漫游以及三维场景旋转时，发现旋转控制效果不理想，出现了偏移，坐标发生错位。

针对上述的问题，本文重点研究和分析了二、三维空间数据同步算法，三维对象运动轨迹处理算法和三维漫游处理算法。

1 二、三维空间数据同步算法

二、三维空间数据同步是三维GIS空间分析的基本功能，基本原理是将二维空间数据与三维模型通过空间坐标进行同步的显示。在小范围的数据中，可以通过坐标实现同步，而面对较大的三维模型和二维空间数据时，当进行三维操作时，二、三维出现明显的坐标偏差和错位，当进行漫游和旋转时，情况会更为严重。

为了让二维空间数据与三维模型数据的同步[8]显示，在通过空间坐标绑定的基础上，结合在二维空间数据的map对象中的地图范围变化事件中绑定三维场景的相机同步控制函数。三维模型显示二维数据需要对相机进行控制，实现的过程比较复杂。本文对二维空间数据控制三维场景相机的位置进行了算法计算。

在三维场景的使用的相机为透视投影相机[9]，因为相机视野中的物体尺寸会随着与相机的距离变远而变小，更接近于人眼观察的效果，所以选用透视投影相机会达到更加逼真的效果。透视相机原理如图1所示。

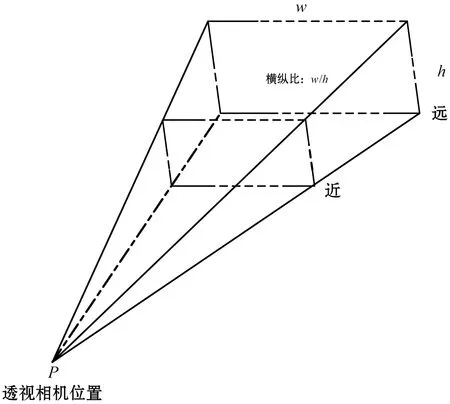
图1 透视相机的观察事物的原理

二维空间数据中的展示的地图相当于三维场景的地面，为了保证相机俯视时看到的效果能与二维地图显示范围一致，必须保证网页中放置map对象的控件元素和Three.js的三维场景scene控件容器元素的长宽比例w/h保持一致。当二维地图显示范围与scene控件显示的地图范围一致时，假设相机的位置为P，相机的视角为θ，此时地面范围的宽度W与相机高度H的关系如图2所示。

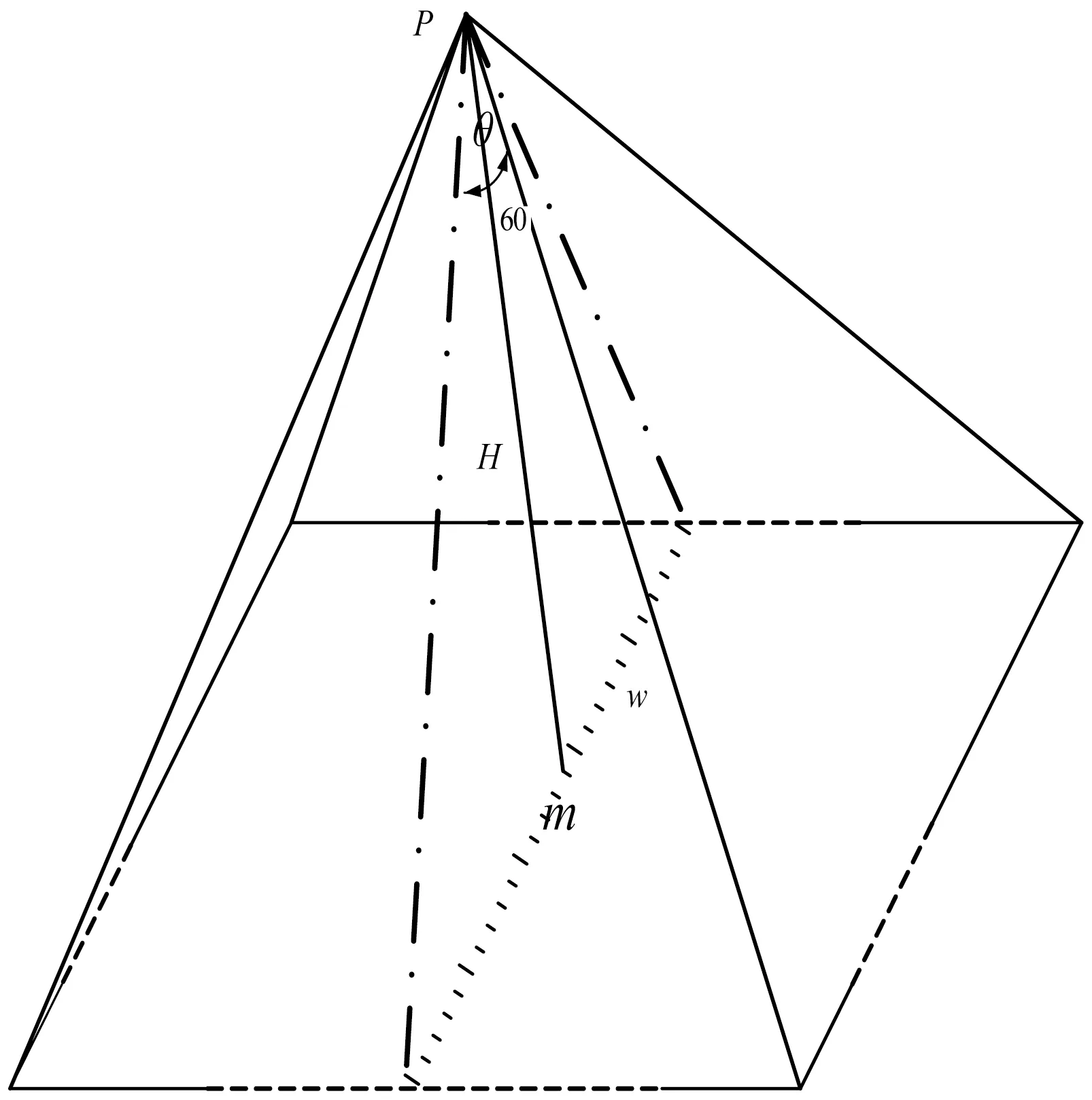
图2 根据地图范围确定相机位置

WebGL场景使用的是右手坐标系，Y轴向上。为了方便计算，将WebGL场景中的XZ坐标作为的经纬度坐标的映射。m(Xm，0，Zm)点为地图范围的中心点，同时也是相机位置P点在地面上的投影点。通过二维地图map控件可以获取到当前显示的二维地图的地理坐标范围，再经过坐标转换得到场景坐标的范围为：

((Xmin,Zmin),(Xmax,Zmax))

可以得到范围中心点的坐标为：

P点坐标的计算公式如下：

(1)

(2)

H、W的计算公式如下：

(3)

W=Zmax-Zmin

(4)

最终计算得到相机位置为：

当三维模型视图与二维空间数据同步时，需要将场景中的相机移动到P点位置并向朝向Y轴负方向。

二、三维空间数据的同步，可以方便将ArcGIS Server服务中的二维地图查询、缓冲查询、编辑、邻近设施分析等功能移植到三维视图，是实现三维数字城市基本功能的基本。

2 三维对象运动轨迹处理算法

物体的运动轨迹主要来自于路径分析结果和二、三维空间数据同步时相机的运动轨迹。这些轨迹都是由分布不均的点集生成的折线，需要对轨迹线进行插值算法分析，使得到的轨迹变得平滑，使物体运动起来更加平缓。本文对运动轨迹进行插值时分别采用了样条函数插值法和CatmullRom样条函数插值法，对物体的运动轨迹进行插值和对比。CatmullRom样条函数[10]与普通样条函数的图解如图3所示。

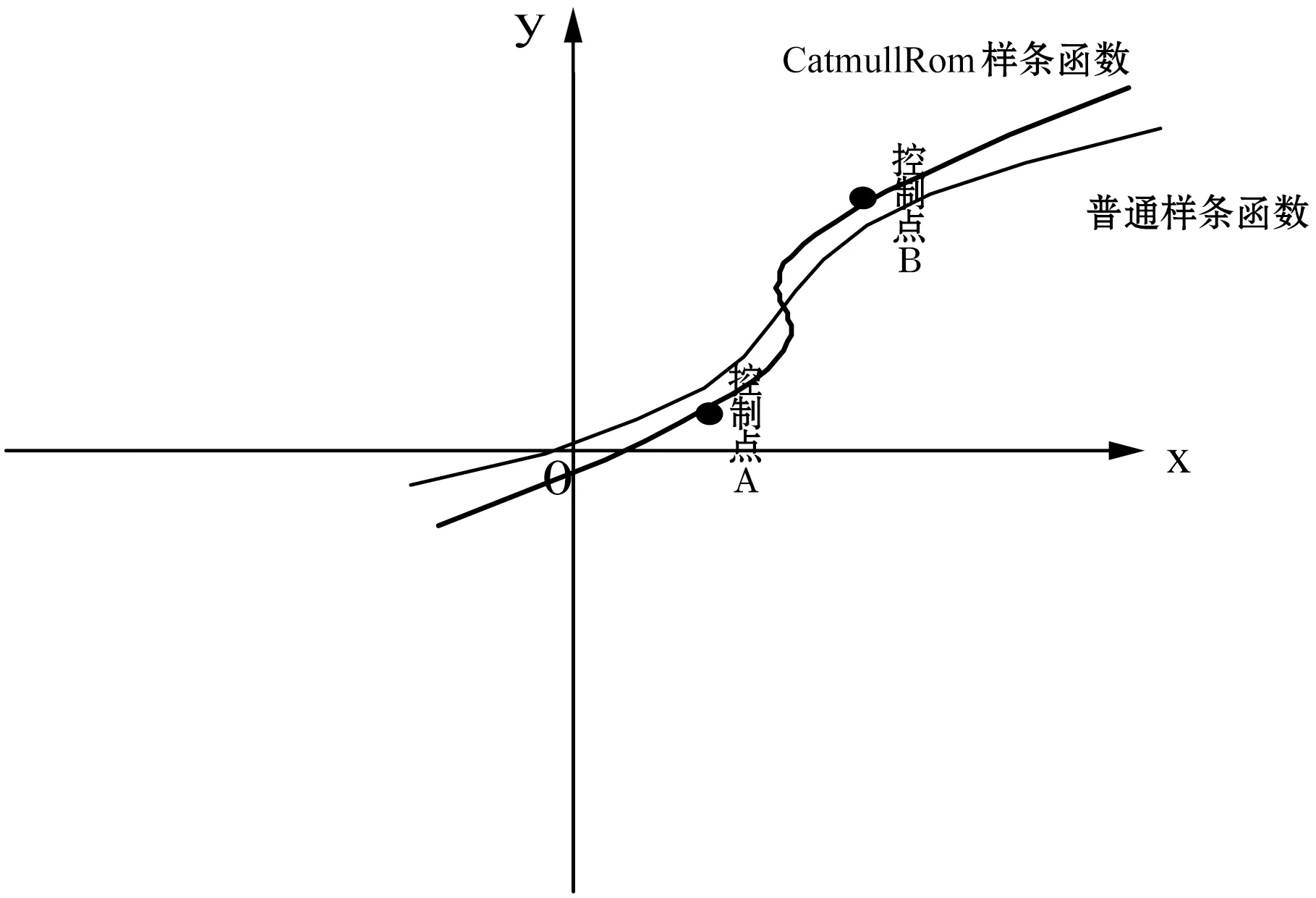
图3 CatmullRom样条函数与普通样条函数对比

可以看出一般的样条函数生成的曲线只会接近控制点，不会穿过控制点，CatmullRom样条函数会穿过每一个控制点，而三维路径分析和漫游需要经过每一个道路线的拐点(控制点)，所以选用CatmullRom样条函数来对物体的运动轨迹进行插值。

插值完成后得到路径为一条平滑的曲线，这时只需在场景渲染时的每一帧读取样条函数上对应的坐标点坐标，再将移动的物体的坐标设置为读取到的坐标，每一帧都执行此操作，就可以实现物体在场景中按照插值轨迹的进行平滑的移动。

3 三维漫游处理算法

三维漫游无非是平移、缩放、旋转等操作，而旋转是实现三维运动处理的关键的部分。旋转的过程是物体从初始状态，经历旋转，达到结束状态。在三维空间中控制物体旋转有三种方式：欧拉角[11]、旋转矩阵和四元数[12]。

欧拉角：这是最直观也最容易理解的旋转表达方式，物体从初始状态到结束状态可以将物体分别绕x、y、z轴按顺序旋转不同的角度完成。一共用三个旋转值和一个旋转顺序表示：

(x,y,z,order)

其中，x、y、z分别表示物体绕x、y、z轴旋转的角度。order表示三次旋转的顺序。当用欧拉角控制[13]对象旋转时其实需要将物体绕三个坐标轴的三次旋转，并且如果旋转的顺序不同得到的结果也不相同，一个欧拉角的参数中包含绕三个坐标轴旋转的角度和三次旋转的顺序四个参数。除了三次旋转中两次为零情况，直接进行线性插值无法得到线性旋转轨迹，也就是说当相机按得到的旋转轨迹旋转时可能会出现抖动的现象，出现这种情况的原因被称之为万向节锁。

旋转矩阵：其实无论经历怎样的旋转物体都可以通过绕一个特定的旋转轴按一定方向旋转一定角度来达到结束状态。也就是绕一个向量旋转一个角度，但是旋转矩阵中变化参数比较多，对于计算和控制状态并不是那么容易。

四元数：四元数描述旋转的原理和旋转矩阵类似[14]，区别就是四元数就引入了复数的思想，对复数进行了延伸，可以把它看成一个四维复数，同样将一个旋转轴和一个绕它变化的角度进行变形，使之成为一个四元数，一共有四个值。这样可以遵循复数的运算，包括加减乘除以及积分等等。

使用四元数法控制物体旋转时物体只需进行一次旋转，所有的旋转是绕着一条直线旋转一定角度。只要指定好这条直线，再指定一个角度即可控制物体的旋转。一个四元数需要的参数有三个直线表达式和旋转的角度值，共含四个参数。四元数旋转坐标表示如下：

{x:kx×sin(a/2),y:ky×sin(a/2),

z:kz×sin(a/2),w:cos(a/2)}

其中，a代表绕轴(kx,ky,kz)旋转的角度)，转换成复数形式为：

cos(a/2)+(kx×sin(a/2))i+(ky×sin(a/2))j+

(kz×sin(a/2))k

这里的i、j、k表示虚数单位，仅仅代表他们分别处于不同的维度，不代表具体值。这样以来就可以实现对旋转进行叠加、加速等效果的控制，计算起来比欧拉角(三次旋转的合成)和旋转矩阵(四元数变形的更多的变量的矩阵形式)更加简单[15]。

通过上面的解释，四元数的表达式可分解为kx、ky、kz、angle，设角度a为angle。而欧拉角的表达式无法分解，设它的表达式为(x,y,z,‘xyz’),‘xyz’只表示顺序不表示数值，因为三个参数都是角度值，具有实际意义无法分解，那么参数有三个，设置让三位场景中的物体绕指定向量匀速旋转，旋转过程如图4所示。

图4 测试对象x,y,z轴的旋转状态

以下四元数表达式各参数和欧拉角表达式各参数数据采集自该对象绕单位向量(0.826 803,0.447 628,0.340 626)匀速旋转一周的不同时间点采集到的参数数值。如表1、表2所示。

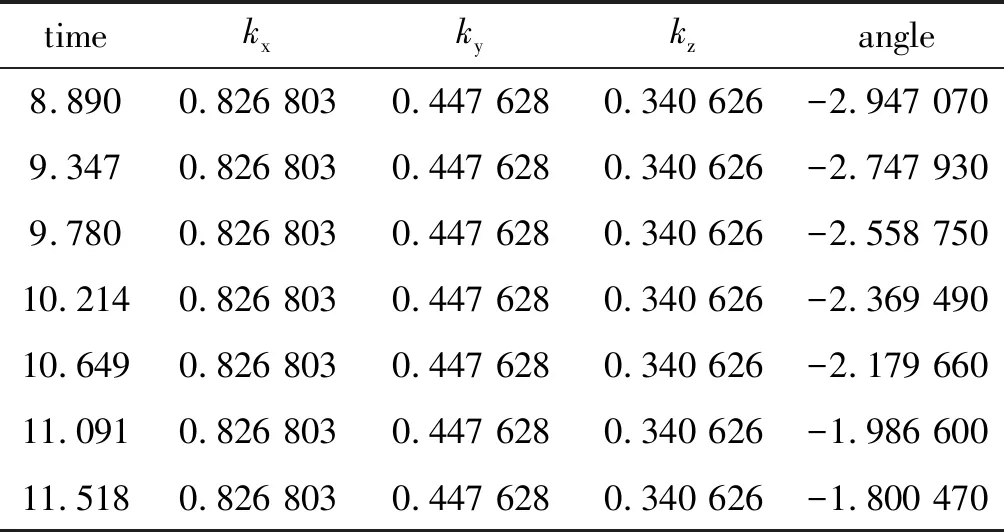
表1 四元数表达式各参数的在旋转中的数值

续表1

表2 欧拉角表达式各参数的在旋转中的数值

续表2

从表1、表2中的数据可以看出，从初始到结束状态四元数表达式和欧拉角表达式各个参数值的变化情况，四元数表达式参数中只有一个角度angle在呈线性变化，而欧拉角的三个参数都在同时进行变化，但是变化规律并不统一。将表1、表2中的数据绘制成数值变化图，如图5所示。

从图5中很直观分析出，四元数可以通过对角度参数进行简单的线性插值就可以实现旋转控制，而使用欧拉角表达式来控制物体旋转状态却不能用简单的线性差值来实现，如果要使用欧拉角来控制旋转，那么就要分别求出每一个xyz每次旋转角度的变化规律，显然复杂程度比四元数高出了很多。

上述的数据只是简单的绕一根轴匀速旋转，是最简单的旋转过程，即使是最简单的旋转过程也很难使用欧拉角表达式通过特定的差值规则来控制旋转，其实物体在实际情景下的旋转过程是多方位的旋转，在转动过程中并不只是在绕某一个旋转轴匀速旋转，而是不断在改变旋转轴和速度。截取一个尽可能短的时间段，可以把这个时间段的旋转近似看成不变的，可以使用四元数表达式和欧拉角来表达此时的旋转，这个动作就可以看成旋转轴在不断旋转，旋转速度不断变化的旋转组合，同时把这些旋转看成旋转轴也在不停地旋转。使用四元数表示旋转，可以使用四元数特有的加减乘除运算法则来计算出每个时段旋转的四元数最终表达，在三维场景中使用这个最终表达来设置物体在对应时段的旋转状态，就可以达到对物体旋转的很好控制，可以对四元数运用一些现有的插值算法来控制物体平滑旋转。而欧拉角并不能够像四元数这样找出规律并应用运算规则，旋转中，欧拉角三个值都在不停变换，仅仅表示一个旋转状态，用来描述和控制物体旋转过程很难找出其特定的规律。

与欧拉角相比四元数描述旋转的优势如下：插值结果为线性轨迹，没有万向节锁，具有唯一表达式。而欧拉角旋转顺序不同会有多种不同的表达式。

选用四元数法来控制物体的旋转，只需要对物体的旋转状态和最终旋转状态的四元数表达式进行线性插值，场景在渲染每一帧时为物体应用每一个插值点的四元数变换，就能保证物体旋转的平滑过渡。

4 实验与分析

本文测试的数据是一个某小城市的数据，范围大小为10平方公里，模型数量超过5 000个，其中矢量面拉伸生成的模型1 421个，导入外部模型3 600多个，按平台设计需要还包含每个建筑物的高程数据、模型参数(路径、大小、旋转)、道路宽度、建筑物名称等必要属性数据。

(1) 二、三维空间数据同步分析 利用二、三维空间数据同步算法计算出二维地图当前显示范围的场景中相机对应的位置，同时利用三维对象运动控制算法对相机的运动过程进行插值计算。让场景中的相机能够动画过渡到根据二维地图显示范围计算出的相机位置。从而实现视图同步。二、三维视图同步效果如图6所示。

图6 二、三维空间数据同步效果

(2) 运动轨迹分析对比 用路径分析生成的路线来测试运动轨迹，图5中展示了采用普通样条插值处理和CatmullRom样条插值处理的不同效果。从图7(a)中可以看出,普通样条插值处理的效果，体现为折线，特别是在转角处的处理比较粗糙，没有完全经过控制点，只是接近。从图7(b)中可以看出，CatmullRom样条插值处理的效果较好，体现了平滑的路径曲线，并且通过了每一个路径坐标控制点。

(a) 普通样条插值处理

(b) CatmullRom样条插值处理图7 三维对象运动轨迹处理效果

5 结 语

本文在基于WebGL的实现三维GIS技术基础上，对二、三维空间数据同步算法、三维对象运动轨迹处理算法和三维漫游处理算法进行了分析和研究。 分析了二、三维视图同步算法的原理，并设计了对应的模型和算法；分析和研究了轨迹处理的算法；详细分析了三维漫游处理算法和实现过程。最终通过实验分析和数据对比，证明了本文设计和研究算法的科学性，同时通过展示的效果，证明了本文研究的场景控制算法达到了预计的效果。本文研究的三维视图算法具有实际应用和研究的价值，实现的技术为三维数字城市的开发提供了技术参考和理论依据。