待定系数法在不等式中的应用
广东省中山纪念中学(528454) 邓启龙
在处理一些复杂的不等式问题时,往往难以直接应用均值不等式或柯西不等式等已有的不等式,这就需要根据题目的结构特点来进行适当的配凑, 待定系数法就这样产生了.本文就来例谈待定系数法在不等式中的应用.
首先给出本文要用到的不等式.
1.均值不等式:
2.柯西不等式:
(1) a1,a2,b1,b2∈R,
(2) a1,a2,a3,b1,b2,b3∈R, (a1b1+a2b2+a3b3)2
3.柯西不等式的推论:
(1) a1,a2∈R,
(2) a1,a2,a3∈R, b1,b2,b3>
下面通过例题来说明待定系数法在不等式中的应用.
首先来看三元不等式中待定系数法的应用.
例1设a,b,c>0,且a2+b2+c2=1,求的最大值.
解由对称性引入参数x ∈(0,1), 则a2+b2+c2=由得
于是

注: 由对称性引入参数,将条件中的a2,b2,c2进行拆分和配凑,然后利用均值不等式,并由系数的比例关系求出参数,进而解决问题.
例2设a,b,c>0,且a2+b2+c2=1,求的最小值.
解引入参数x>0,则

接下来看二元不等式中待定系数法的应用.
例3设a,b>0,且求a2+b2的最小值.
解假设当a=x,b=y 时, a2+b2取最小值, 引入参数由a3+x3+x33x2a得同理可得所以由x3: y3=8 : 1且得x=10,y=5.于是a2+b2所以a2+b2的最小值为125,当且仅当a=10,b=5 时取最小值.
注: 通过假设a2+b2取最小值时a,b 的取值引入参数,并利用结构特点和取等条件构造不等式,最后由系数的比例关系和参数满足的条件求出参数,进而解决问题.
例4设a,b>0,且a+2b=1,求的最小值.
解假设当a=x,b=y 时,取最小值,引入参数x,y > 0,且x+2y=1.由a2+x22xa 得a22xa−x2,同理可得b22yb−y2.所以

5000y5−7000y4+3250y3−500y2+36y−9=0,解得于是
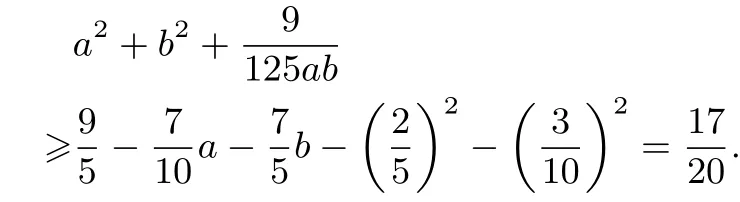
例5设a,b>0,且求的最小值.
解假设当a=x,b=y 时,取最小值,引入参数x,y >0,且得同理可得所以

由(1−2x3):(1−2y3)=(−20):1 且得于是
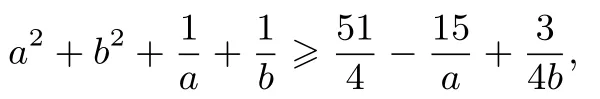
例6设a,b>0,且a+2b=1,求的最大值.
解引入参数x ∈(0,1),由

得
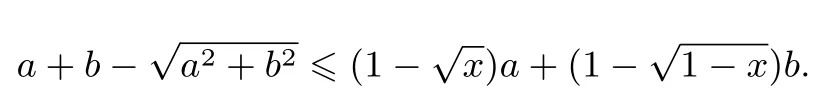
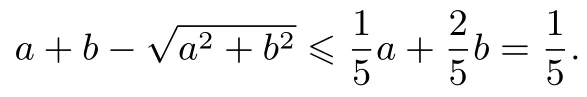
以上的例子都是有两个或三个变量的不等式问题,其实求函数最值也可以利用不等式,若不能直接应用均值不等式或柯西不等式,则可以引入参数,应用待定系数法解决问题.下面给出两个例子,说明待定系数法在求函数最值中的应用.
例7设x>0,求函数的最小值.
解引入参数λ>0,由
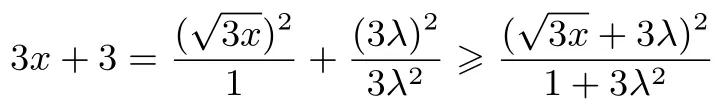
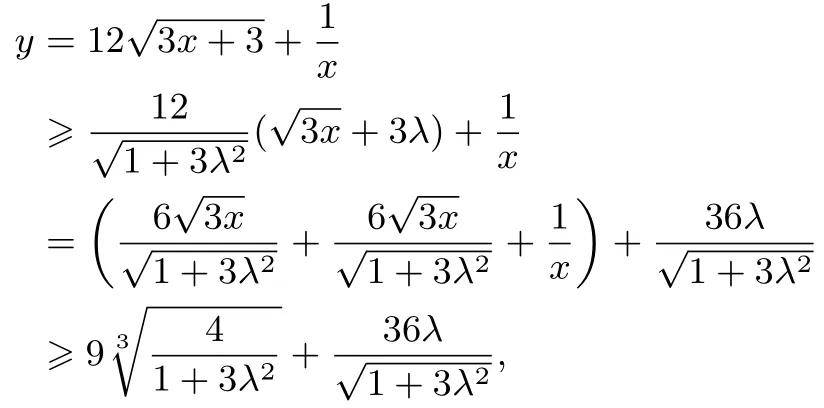
例8求函数的最大值.
解引入参数λ,µ>0,
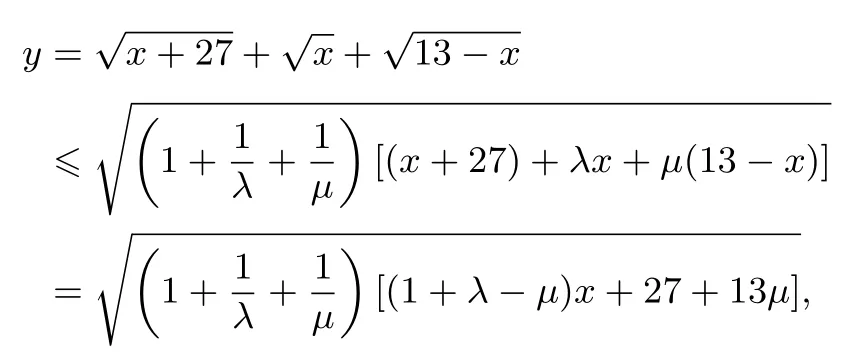
由取等条件得
x+27=λ2x=µ2(13−x), 且 1+λ−µ=0,消去x,µ 得13λ4+26λ3−54λ2−80λ−40=0, 解得λ=2,µ=3,x=9.于是