巧用数形结合解题

广东省佛山市罗定邦中学(528300) 龙 宇

我国著名数学家华罗庚曾说过:“数缺形时少直观,形少数时难入微;数形结合百般好,隔离分家万事休”.数学中,数和形是两个最主要的研究对象,它们之间有着十分密切的联系,在一定条件下,数和形之间可以相互转化,相互渗透.

数形结合的基本思想,就是在研究问题的过程中,注意把数和形结合起来考察,斟酌问题的具体情形,把图形性质的问题转化为数量关系的问题,或者把数量关系的问题转化为图形性质的问题,使复杂问题简单化,抽象问题具体化,化难为易,获得简便易行的成功方案.

1.构造三角形

(1) 利用正、余弦定理构造三角形

利用三角形的正、余弦定理,可将某些算式转换为三角形的边及角度问题.

例1设正实数a,b,c 满足求a,b,c 的值.

解析如图1: 以点O 为出发点, 做长度为a,b,c 的三条边长OA, OB, OC, 且使得∠AOB=90◦,∠AOC=120◦,∠COB=150◦.结合余弦定理可得:所以∠CAB=90◦, 过O 作OM⊥AC,ON⊥AB.设AM=m, AN=n.又由∠ABO =∠OAM, 所 以即有在△AOC 中, tan(∠OAC+∠OCA)=tan 60◦=即有:化简得:所以

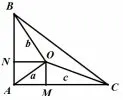
图1

例2已知非负实数a,b 满足3a2+ab+b26,求M =a4+b4的最值.

解析设a2+ab+b2=c2,3c26, 可转换为c2=a2+b2−2ab cos 120◦,可以视为由a,b,c 构成一个最大角为120◦的三角形.如图2 所示:设∠B =θ,

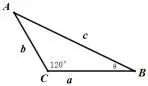
图2

原问题就转换为求函数: f(θ)=sin4+sin4θ =sin4θ+cos4的最值.对函数求导得:

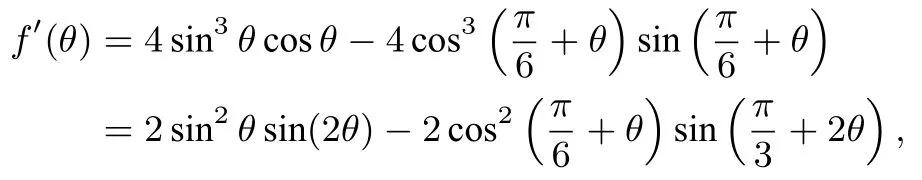
其中:

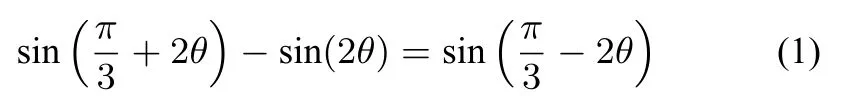
变式读者也可在题干的条件下,求a+2b,a2+b2等的范围.

(2) 利用向量构造三角形

例3已知|a|=2,向量b 满足2|b−a|=b·a,当b,a的夹角最大时,求|b|的值.

解析如图3,设因 为b · a=|b| ·且 有|a|=2可得:由2|b−a|=b · a 可 得:其中表 示 向 量b 在 向 量a 方向上的投影.连接点A,B, 过点B 作OA 的垂线, 垂足为C.即有|OC|=|AB|.设|OC|=|AB|=x ∈(0,2], 在Rt△OBC 及Rt△CBA 中分别使用勾股定理得:|OB|2=|OC|2+|BC|2=|OC|2+|BA|2−|AC|2, 即有b2=x2+4x−4,显然可得当x=|OC|=|AB|=2 时,|b|取到最大值

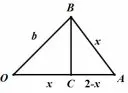
图3

(3) 利用距离公式构造三角形

例4(2016年全国高中数学联赛辽宁预赛,3)函数

则f(x,y)的最小值为____.

解析化简f(x,y)的表达式得:

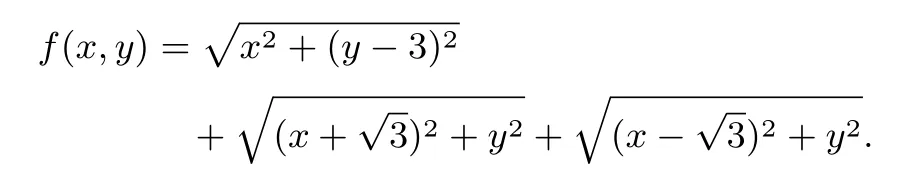
2.构造圆锥曲线

(1) 构造圆

例5(2013年高中数学联赛, 7) 若实数x,y 满足则x 的取值范围是______.

解析令b(a,b0),此时x=a2+b2.条件中的等式化为: a2+b2−4a=2b,整理得:(a−2)2+(b−1)2=5(a,b0).如图4,在平面aOb 中,点(a,b) 的轨迹为以(2,1) 为圆心,为半径的圆在a,b0 的部分, 即点O 与弧ACB的并集.而表示点(a,b) 到原点的距离, 所以所以x=a2+b2∈{0}∪[4,20].

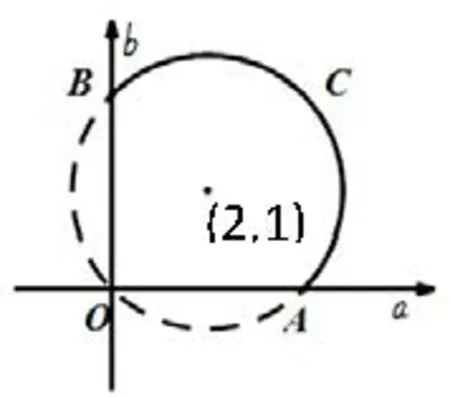
图4

(2) 构造椭圆

例6(2013年高考课标全国卷I 理科第12 题) 设△AnBnCn的三边长分别为an,bn,cn, △AnBnCn的面积为Sn,n=1,2,3,···.若b1>c1,b1+c1=2a1,an+1=an,则( ).

A.{Sn}为递减数列

B.{Sn}为递增数列

C.{S2n−1}为递增数列,{S2n}为递减数列

D.{S2n−1}为递减数列,{S2n}为递增数列

解析因为an+1=an=an−1=···=a1, 所 以△AnBnCn的一个边是固定的, 又因为可通过数学归纳法证得: bn+1+cn+1=bn+cn=···=b1+c1=2a1.即△AnBnCn另两条边之和为定值.如图5,对△AnBnCn而言,以BnCn的中点O 为原点,OCn为x 轴,过O 做OCn的垂线为y 轴.点Bn的坐标为点Cn的坐标为设点An的坐标为(x,y),因为AnBn+AnCn等于定值,所以点An的轨迹为椭圆(去掉两个端点).显然可得:所以当n 增大时,点An向椭圆的上顶点靠近,所以{Sn}为递增数列.

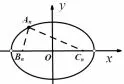
图5

(3) 构造抛物线

例7求函数的最小值.

解析构造点

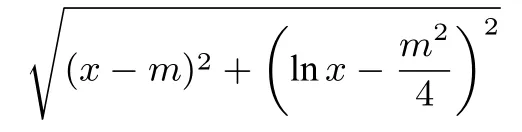
3.构造基本初等函数

例8(2009年高考辽宁卷)若x1满足2x+2x=5,若x2满足2x+2 log2(x−1)=5,求x1+x2的值.

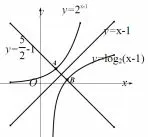
图6

分析观察两方程可知,两方程都是超越方程.所以不可能分别将x1,x2求解出来.对两个方程变形: 2x+2x=5 ⇔2x=5−2x ⇔2x−1=2x+2 log2(x−1)=5⇔2 log2(x−1)=5−2x ⇔log2(x−1)=如图6,x1即是曲线f(x)=2x−1与曲线交点A 的横坐标,x2即是曲线g(x)=log2(x−1)与曲线h(x)交点B 的横坐标.且有曲线f(x) 与曲线g(x) 关于直线l :y =x−1 对称.显然直线h(x)与直线l 相互垂直.即有点A 与点B 关于直线l 对称.联立h(x)与l 求得交点即有

例9(2008年高考重庆卷理科) 求函数f(x) =的值域.

分析此题在当时是以选择题的形式出现的,也许是出题者考虑到本题的难度, 考生可以通过“特殊值”法选出答案.如果应用导数求解,计算过程复杂,且不易发现极值点.改变题目的形式,应用其几何背景构造三角函数求解.

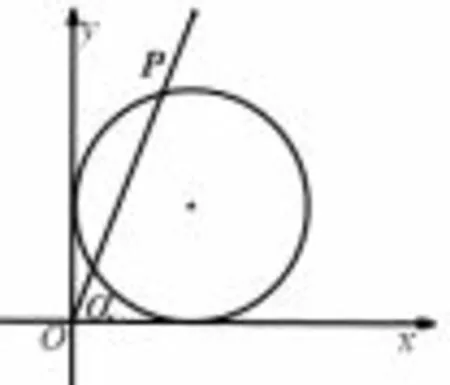
图7

解析3−2 cos x−2 sin x=(1−sin x)2+(1−cos x)2,设点(1−sin x,1−cos x)为点P(m,n),则有点P 的轨迹为圆可以表示为以OP 为终边的角的正弦值的相反数即−sin α.如图7 所示:−sin α ∈[−1,0],所以f(x)的值域为[−1,0].

4.构造直线

例10已知求tan α 的值.

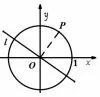
图8

解 析由化简得:表示点P(sin α,cos α) 到直线l :的距离为1.如图8: 点P ∈圆x2+y2=1.当OP⊥l 时, 点P 到直线l 的距离为1.因为即有所以tan α=

5.练习

2.设x,y,z >0.证明:

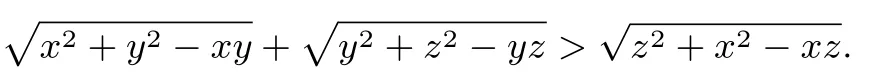
提示: 构造三角形,利用边长基本关系: 两边之和大于第三边.

3.(2018年浙江省温州市摇篮杯高一数学竞赛,9)已知平面向量满足若t ∈[0,1],则有的最小值为______.

4.(第十八届加拿大国际数学奥林匹克竞赛试题)求所有的实数x,使得

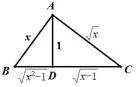
图9