基于EMD-RVM的短期光伏发电系统功率预测

桑康伟，王 坤，高文根

（检测技术与节能装置安徽省重点实验室，安徽工程大学，安徽 芜湖241000）

引言

随着能源短缺与环境污染问题的日益突出，光伏发电作为一种清洁的可再生能源得到了快速的发展，但由于外界不确定因素的影响使它具有波动性、间歇性等缺点，大规模的光伏并网会对电力系统的安全和稳定运行造成影响。因此，提高光伏发电功率预测的精确度对系统安全稳定运行、维护电能质量和太阳能的有效利用具有重大意义［1］。

根据国内外光伏发电预测方法的研究可知，光伏发电预测方法一般可分为基于系统输出功率的直接预测和基于太阳辐射强度的间接预测两大类。文献［2］利用天气数据将天气类型划分为晴、阴、多云和雨四类，建立SVM预测模型，选出与待预测日特征相似的相似日数据集进行训练，然后预测未来一天06∶00～19∶00每小时输出功率，预测的误差为10%～20%。文献［3］利用动态贝叶斯网络建立预测模型对未来一天各时刻的发电功率进行预测，该模型可以有效地反映出不同影响因素间的内在联系，预测精度比较高，但当预测日天气类型发生较大改变时预测效果会明显下降。文献［4］利用改进后的BP神经网络建立预测模型，把历史相似日输出功率数据值、历史气象信息和待预测日气象信息当作输入变量对输出功率进行直接预测。以上的预测方法在短期光伏发电功率预测中普遍具有预测精度不高的缺陷，尤其在早、晚或者下雨天气时预测误差较大。

经验模态分解（Empirical Mode Decomposition，EMD）是一种新的自适应信号时频处理方法，特别适用于分析处理非平稳、非线性数据序列的复杂信号，它可以依据信号自身的特点自适应地产生合适的表示函数，而不需要提前选择基函数，这些函数可以较好地反映信号的本质和真实信息［5］。相关向量机（Relevance Vector Machine，RVM）是2001年由Tipping在贝叶斯框架的基础上提出来的，它不仅具有支持向量机的一些优点，同时，也弥补了支持向量机的一些缺点，如RVM提供了概率解释，不需要估计正则化参数，其核函数也不需要满足Mercer条件，需要更少的相关向量等［6］。因此，本文借鉴文献［7］的思想，提出了一种把EMD与RVM相结合的光伏发电功率预测方法（EMD-RVM）。首先把历史输出功率数据依据天气类型进行归类，用欧氏距离筛选出待预测日的相似日数据，随后用EMD将原始光伏发电输出功率序列分解成不同频率且相对稳定的本征模态函数（IMF）分量，再对各个IMF分量分别建立RVM模型进行预测，最后将各分量的预测值等权值求和得到最终的预测值。

1 EMD与RVM理论基础

1．1 经验模态分解

经验模态分解（EMD）是1998年由Norden E.Huaug等人提出的，它将信号分解成不同频率的本征模态函数（IMF）。通常认为本征模态函数IMF需要满足两个条件：（1）在整个信号上，极值点的数量和过零点的个数相等或至多相差一个；（2）在任何时候，由局部极大值和局部极小值点分别形成的上、下包络线的均值为零，也就是说，上包络线和下包络线相对于时间轴局部对称。其分解流程如图1所示，具体步骤为：

（1）假设原始信号是x（t），找到所有局部极大值和局部极小值点，并将所有局部极大值点用三次样条函数连接作为上包络线，连接所有局部极小值点得到下包络线，上、下包络线包含了全部数据。

（2）求出上、下包络线的均值m1，原始信号x（t）与m1差为h1＝x（t）－m1。如果h1是IMF，那么它就是第一个分量。

（3）若h1不是IMF，那么将h1当做原始信号处理，再一次进行上述步骤，便可得到h11＝h1－m11，m11即是h1上包络线与下包络线的均值。经过反复筛选k次以后，若h1k满足了IMF的条件，那么它就成为IMF，即h1k＝h1（k－1）－m1k，c1＝h1k是原始信号的第一个IMF成分，代表x（t）最高频率的分量。

（4）从x（t）中可分离出c1，然后得到r1＝x（t）－c1。把r1当作原始信号重复进行上述过程，便能够得出信号x（t）第二个IMF成分c2。重复上述过程n次，便能够得出n个IMF分量：r2＝r1－c2，…，rn＝rn－1－cn，当rn是单调函数或是一个极小的常量时，就表明无法再提取IMF分量，分解过程结束，得到：

式中：残差rn是信号向x（t）的集中趋势，IMFs（c1，…，cn）分别包含了不同时间特征尺度的信号分量，它们的尺度由小到大，因此，各分量便包含了从高到低的不同频率段的成分。每个频率段所含有的频率成分是不一样的，它们随x（t）的改变而改变。

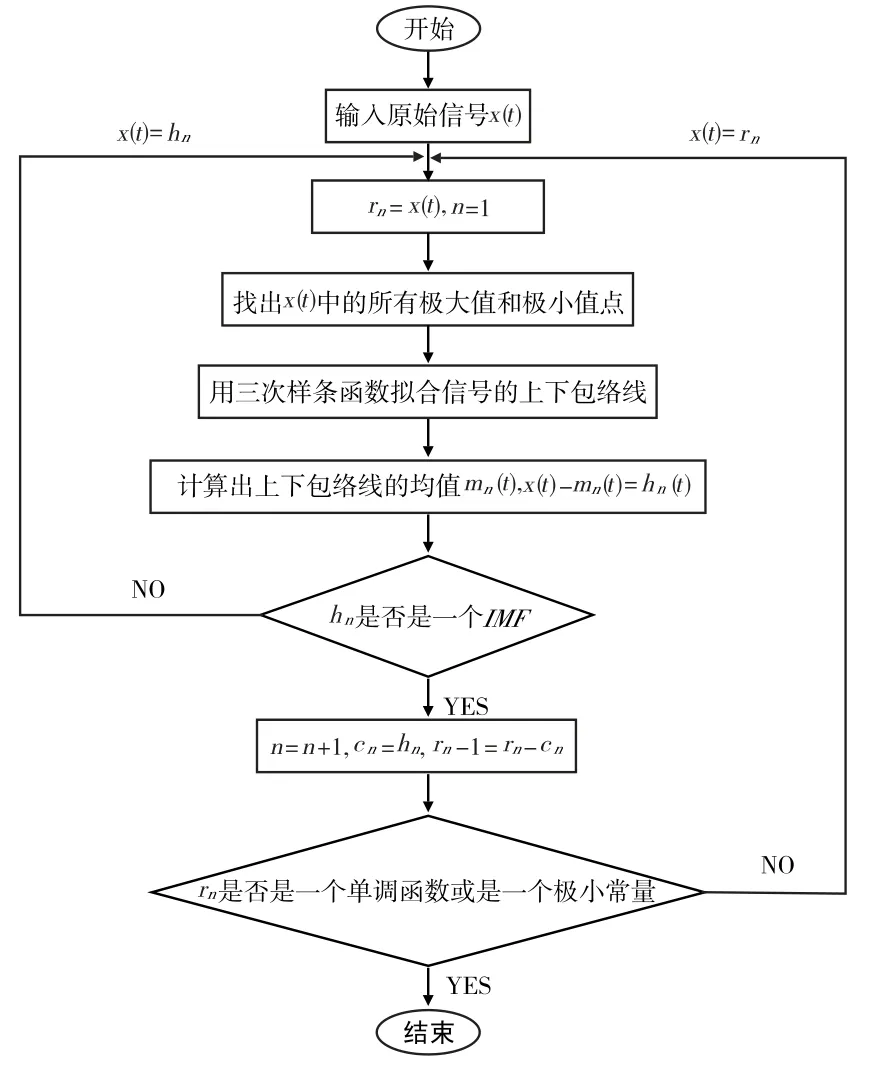
图1 EMD算法流程图

1．2 相关向量机

相关向量机（RVM）是在2000年由MicnaclE.Tipping提出的一种和支持向量机（Support Vector Machine，简称SVM）类似的稀疏概率模型［8］。它不仅拥有SVM的优点，还弥补了SVM的不足之处，如RVM在选择核函数时不受梅西定理的限制，可以构建任意的函数；不需要人为设置惩罚因子，参数自动赋值；RVM稀疏测试时间较短，更适合用于在线预测，这些对解决实际问题具有重要意义［9］。RVM基本原理为：

给出训练样本集｛xn，tn｝Nn＝1，其中x是N维输入向量，t是输出标量，则定义RVM回归模型为：

式中：ω是权参数向量，ω＝（ω0，ω1，…，ωN）；ξn是服从Gamma分布的零均值高斯噪声，其方差是σ2；核函数φi（x）≡K（x，xi）。

假设tn是相互独立的，那么训练集的似然函数为：

p（t／ω，σ2）＝

式中：

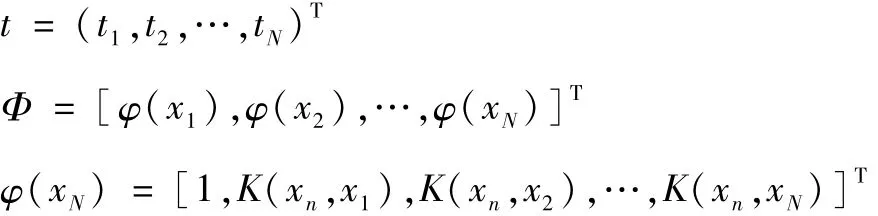
模型中有较多参数，通过式（3）把似然函数最大化求得的参数ω和σ2容易出现模型过学习，因此，利用稀疏贝叶斯原理赋予ω零均值高斯先验分布，可得：

式中：α为N＋1维的超参数向量，这样每个权重都会和一个超参数单独对应，进而控制各参数受到先验分布的影响，确保了相关向量机具有稀疏性。

在定义完先验概率分布和似然分布之后，依据贝叶斯原理推导便能求得全部未知参数的后验概率分布，即：

令A＝diag（α0，α1，…，αN），则后验协方差矩阵表示为：

通过迭代算法求得超参数的最优值来确定模型权值，即：

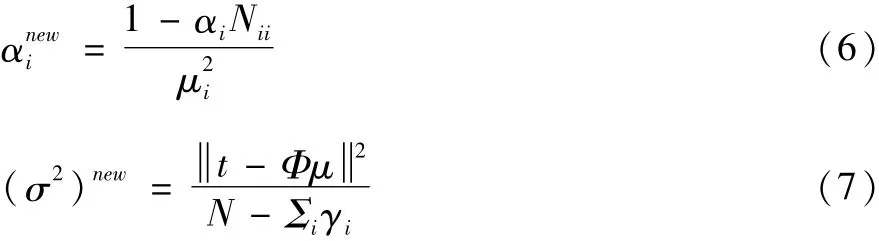
式中：μi表示第i个后验平均权；Nii表示后验协方差矩阵中的第i个对角元素；N表示总体样本数据的个数。

若设定x为新的输入值，那么对应的输出概率分布服从高斯分布，即：

式中：预测均值y*＝μTφ（x*），即为t*的预测值。

2 EMD-RVM预测模型

预测模型将用到日最高温度、日最低温度、日期、光伏发电输出功率值等数据。由于光伏发电系统的输出功率会受到天气变化的严重影响，所以本文依据天气类型把光伏发电输出功率分为晴天、晴转多云（多云转晴）、多云、阴天、雨天（雪天）五种类型［10］，从而得到五种历史数据集；然后筛选出和待预测日天气类型、日期、气温等数据相似的日期作为相似日，再通过相似日数据进行预测，从而提高模型的预测精确度［11］。

由于光伏发电系统具有一定的随机性、间歇性，因此其输出功率为非平稳信号。本文利用EMD对原始信号进行分解，可得到若干个IMF分量，从而可明显地反映出原光伏发电系统输出功率的周期性、随机性、趋势性；进而很好地掌握原始信号的特性，如图2所示。

综合光伏发电系统输出功率具有间断性、不确定性和周期性等特点，另外，系统输出功率与各个影响因子之间表现为非线性关系［12］，因此本文首先利用RVM对所有IMF分量在各时刻t进行预测，然后对所有IMF分量t时刻的预测值等权值求和，即可得到光伏发电系统在t时刻的输出功率预测值。

图2 EMD分解图

本文根据所研究的发电站实际情况，定义06∶00～20∶00为发电站的系统功率输出时间段。每次采集数据的时间间隔为15 min，可得到57个数据点，建立模型步骤如下：

（1）数据处理

由于本文中利用的数据取值范围相差大且单位不同，因此把数据通过公式（9）进行归一化处理，可以使全部数据统一到相同参考范围内，进而使预测的效率及精确度得到提高。

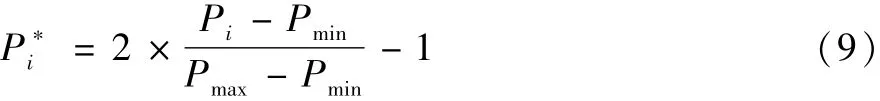
式中：Pi表示第i个时间点（1≤i≤57）的功率输出值；Pmax和Pmin为输出功率序列中的最大值和最小值；P*i为归一化的功率序列值。

通过公式（10）可对温度数据进行归一化处理。

式中：T为待处理的温度值；Tmax和Tmin为温度序列中最大值与最小值；T*为处理后的温度序列值。

对日期的归一化公式为：

式中：n为年序日。

（2）通过EMD对归一化处理后的系统输出功率数据进行分解，根据经验模态分解终止准则最多可得到IMF1、IMF2、IMF3、IMF4、IMF5以及R6等六个分量。

（3）筛选出相似日数据

D为包含相同类型的n天历史数据集合，通过公式（12）可得待预测日i的欧氏距离集合为｛di1，di2，…，dik，…，din｝，然后将该集合中的数据从小到大排序，筛选出和待预测日最相似的5天历史数据用来模型训练［13］。

式中：Xi1、Xi2、Xi3分别为待预测日的最高温度、最低温度以及日期；Xk1、Xk2、Xk3分别为样本集合中第k天的最高温度、最低温度以及日期。

（4）模型训练

对分解后的每个IMF分量分别利用RVM预测模型采用多输入、单输出方法进行预测。以晴天为例，利用RVM模型对IMF1分量在t时刻的输出值IMF1（t）进行预测，训练过程如图3所示。

图3 RVM1（t）训练流程图

图3 中，IMFi（1，1，t）、IMFi（1，2，t）、IMFi（1，3，t）、IMFi（1，4，t）和IMFi（1，5，t）为晴天样本集中与待预测日最相似的5天所对应t时刻的IMF1分量值，其中1≤t≤57。经过较多数据训练后，可得到晴天t时刻IMF1的预测模型RVM1（t）。同理可得其他天气类型下的预测模型。

（5）预测流程

通过以上步骤可得到与待预测日同天气类型下t时刻的各分量预测值为IMF1（t）～IMF6（t），随后将各预测值进行等值加权求和，最后再进行反归一化可得到待预测日对应t时刻的预测值，如图4所示。

图4 EMD－RVM预测流程图

图4中，IMF（1，β，t）～IMF（6，β，t）是五个相似日数据的不同IMF分量对应t时刻的数据集合，其中1≤β≤5，即为5个相似日。

3 实例分析

本文的历史发电数据来源于国内某一装机容量为400 kW的光伏发电站，文中所用到的训练数据是2013－2015年每日气象数据和每日06∶00～20∶00采样的57个光伏出力数据。为了验证建立的预测模型，将2016年的光伏出力数据当作测试数据。本文选用2016年2月5日、5月14日、8月8日、10月24日以及12月19日当作待预测日，把每日最高温度、每日最低温度、日期、5个与待预测日天气类型一样的相似日数据用作模型的输入，进而预测待预测日的光伏发电系统输出功率，预测结果如图5所示，图中实线为光伏发电系统的实际输出功率值，虚线为作为对比的小波-LSSVM预测模型的预测值，“*”线为本文建立的EMD-RVM预测模型的预测值。

图5 光伏发电系统输出功率预测结果图

然后利用通过公式（14）与公式（15）计算得到的归一化平均相对误差（MRE）和归一化均方根误差（RMSE）来对预测的效果进行评价，见表1。

式中：Pforecasting为光伏出力预测值；Ptrue为光伏出力真实值；Ptotal为光伏发电站装机容量值；t为时间；N为预测值样本数。

表1 预测误差比较

从图5和表1可知，相对小波-LSSVM而言，利用本文方法求出来的相对误差较小，且波动范围不大；本文方法的平均MRE误差范围为2.21%～9.18%，平均值为4.06%，而小波-LSSVM方法的平均MRE误差范围为2.32%～17.12%，平均值为9.03%；本文方法的平均RMSE误差范围为2.92%～12.82%，平均值为5.66%，而小波-LSSVM方法的平均RMSE误差范围为2.75%～18.24%，平均值为10.20%；用单一RVM方法预测得到的误差值也皆大于本文方法的同类型误差值。因此，较小波-LSSVM和单一RVM两种方法而言，本文所提出的预测方法的预测精度更高，且能够较好地应用于非线性、非平稳时间序列预测。

4 结论

（1）相似日期的光伏出力曲线具有很高的相似性，本文考虑了相同天气类型的日最高温度、日最低温度、日期数据等因子，然后采用欧氏距离从样本集中筛选出5个相似日数据对模型进行训练，可使预测精度得到一定的提高。

（2）利用经验模态分解法对历史发电数据序列进行平稳化处理得到多个IMF分量，能够突显原始序列的局部特征，并且可以减少不同特征信息间的相互干扰，进而可以减小建模的难度。

（3）分别对各个IMF分量建立RVM预测模型，然后将各分量对应时刻的预测值进行求和可得到最终的预测值，这样可以把光伏发电站输出功率的非线性与非平稳性对预测结果的不良影响大大降低。

（4）实例验证结果显示EMD-RVM能够有效地预测光伏发电系统的输出功率，与小波-LSSVM方法相比较，其预测精度更高，且误差范围更小。