基于电价响应模型的电动汽车充电优化策略

汝改革，刘世林，陈 徽

（检测技术与节能装置安徽省重点实验室，安徽工程大学，安徽 芜湖241000）

引言

随着化石燃料枯竭和环境问题的不断加剧，电动汽车作为新能源汽车，在减少环境污染和温室气体排放方面有巨大潜力［1-2］。然而，随着接入电网充电的电动汽车的数量增多，电动汽车的充电计划安排不合理可能会对电网系统的安全运行和经济效益产生较大影响［3］。因此，合理安排电动汽车有序充电成为当前的主要研究趋势。目前，国内外学者提出了许多有序充电的研究方法，归结起来主要分为两种：直接负荷控制和电价指导控制。

第一种方法由配电网调度中心或充电站控制充电桩的充电功率大小，在满足系统安全和车辆充电需求的基础上进行有序充电。文献［4－5］通过分析影响电动汽车充电负荷的因素，建立了考虑电动汽车充电不确定性的电网调度优化调度模型。文献［6］提出了插电式混合动力汽车充电对日负荷曲线和配电网线损影响的优化策略。文献［7］提出了在线控制和离线控制两种模式相结合的充电控制方法，通过控制充电功率进行有序充电。

第二种方法是基于经济激励引导电动汽车响应电价机制有序地接入电网，减少电网的峰谷差，降低充电站的控制难度。文献［8－11］中，考虑到用户对电价的响应规律，构建了峰谷电价优化模型，以引导电动汽车用户在低谷时段充电，减少用户的充电成本，同时削减电网的负荷高峰。大部分文献考虑了充电成本和控制难度方面，却未提及小区变压器容量和用户满意度的问题。文献［12－14］提出了一种有序充电控制方法，在不增加变压器容量的情况下满足电动车辆的充电需求和用户满意度。文献［15－16］在充分考虑了用户的充电需求、充电起始时刻、变压器容量等约束条件的基础上，提出了一种充电站有序充电调度的优化策略，提高了配电网运行的稳定性。

本文与以上论文的不同之处在于，在充分满足电动汽车用户和电网需求的同时，又保证了充电站在优化前后收益不受损的情况下，制定了保证用户侧、电网侧以及充电站侧三方共赢条件下的电价定价模型。该优化模型不仅减小了电动汽车充电对配电网负荷的影响，还降低了电动汽车用户的充电成本，有利于能源节约方面控制策略的发展研究。

1 电动汽车充电需求特性

大规模的电动汽车接入电网，根据用户的充电习惯、用车习惯、以及用户对充电电价的承受程度，通过数据统计结果，可得到近似的分布规律。采用2011年美国交通部对全美家用车辆出行进行统计的结果［17］，将数据归一化处理，结果显示，电动汽车接入充电站时刻和出站时刻均服从正态分布，平均电动汽车每日行驶里程数服从对数正态分布。

电动汽车接入充电桩的充电时刻，概率密度函数为：

式中：x为起始充电时刻；μs＝17.6；σs＝3.4。

电动汽车离开充电站后的时刻，即电动汽车拔掉充电桩时刻，其概率密度函数为：

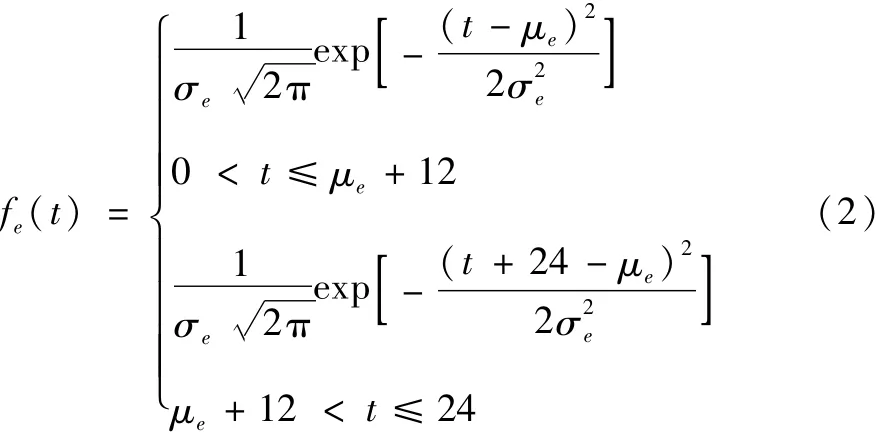
式中：t表示充电结束时刻；μe＝9.24；σe＝3.16。

电动汽车的日均行驶里程数，即电动汽车每日出行行驶距离服从对数正态分布，其概率密度函数为：

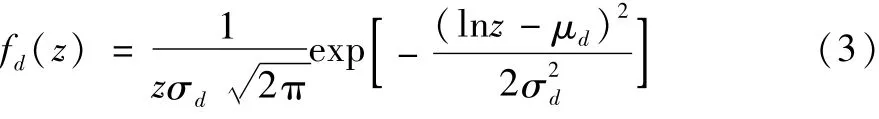
式中：z表示电动汽车日行驶里程；μd＝3.2；σd＝0.88。

充电站根据每辆电动汽车的荷电状态以及车主所需要的期望状态来安排相应的充电计划，保证在充电结束后达到用户的充电需求。

式中：Tc为电动汽车充电所需时长；d为电动汽车的日行驶里程；E100为电动汽车行驶100 km的耗电量；Pc为电动汽车充电功率。

在无引导机制情况下，电动汽车处于无控制充电状态。设置εt＝1表示电动汽车处于充电状态，εt＝0表示电动汽车处于非充电状态，即电动汽车t时刻充电概率为：

式中：FTSTC表示电动汽车处于充电状态下的概率分布函数；PE，t表示一台电动汽车在t时刻的充电功率。

本文采用蒙特卡洛模拟法模拟电动汽车1天内充电情况，并计算出电动汽车无序充电和有序充电下的充电负荷。通过模拟仿真结果发现，有序充电对电网合理运行有积极作用。

2 电动汽车有序充电模型

2．1 有序充电目标函数

本文从提高系统稳定性以及能源节约的角度出发，与传统有序充电模型中以功率为控制量不同，提出的模型以每时段的电动汽车充电投入数量为控制变量，选择负荷峰谷差最小为优化目标，通过将1天划分为96个控制时间段，在每个时间段的尾部时刻接入电动汽车的充电计划。有序充电控制策略目标函数为：

式中：LP－V为负荷峰谷差；i、j分别代表负荷最高时刻和最低时刻；L0，i为时段i的常规负荷；PE，i为电动汽车时段i内的充电功率；ai表示第i时段充电站电动汽车充电数量；Pc为电动汽车的充电功率。

2．2 有序充电控制约束条件

（1）电动汽车充电数量约束：任意时刻处于充电状态的电动汽车数量不能超过电动汽车总数量。

式中：N为电动汽车总充电数量。

（2）变压器容量的约束：电动汽车的充电负荷与基本负荷之和需小于配电网变压器可用容量。

式中：Ptrans表示系统变压器容量。

（3）电动汽车充电需求的约束：电动汽车充电结束时的荷电状态不小于用户期望的荷电量。

式中：Ssoc，k表示第k辆电动汽车充电完成后的荷电状态。

2．3 优化模型求解

采用遗传算法对优化模型进行求解，以15 min作为时间间隔，一天分为96个时间段，编码为96个编码基因，负荷峰谷差作为遗传算法的适应度函数，比较每个个体的适应度值，采用最小适应度值代替所有种群的适应度值，同时保留最小适应度值下的每时段最优状态下的电动汽车充电数量，通过各时段充电数量得出整天的负荷曲线。具体计算过程如图1所示。

图1 遗传算法求解流程

电动汽车的最优充电策略将决定控制目标下的充电负荷分布，可以为引导电动汽车群体进行有序充电的分时电价机制制定研究方案。

3 基于电价响应的充电站经济调度模型

3．1 基于峰谷分时电价用户侧响应模型

根据电量与电价的响应关系，假设电动汽车用户对充电电价的变化高度敏感，则充电时段电价下降时，用户充电数量随着增加，充电时段电价上升时，电动汽车充电用户数量减少。所以，充电站设置合理的充电电价至关重要，不仅可以引导电动汽车用户合理充电，降低充电站管理难度，同时用户充电成本也会降低［18］。

式中：Qf、Qp、Qg分别表示实施分时电价后的峰、平、谷各时段充电电量；Q1、Q2、Q3分别表示在固定充点电价时段下的充电电量；ΔC1、ΔC2、ΔC3分别表示实施分时电价前后时段的电价变化量；C为实施前的充电电价。

建立电动汽车充电数量与充电站提出的充电电价之间的联系，主要依靠电量电价规律来确定。依照用户的电动汽车充电习惯，大多数用户选择在电价较低时段进行充电，充电时段的电价越低，电动汽车充电数量也会越多，因此，在负荷峰谷时段下的充电电价与电动汽车充电数量之间关系为：

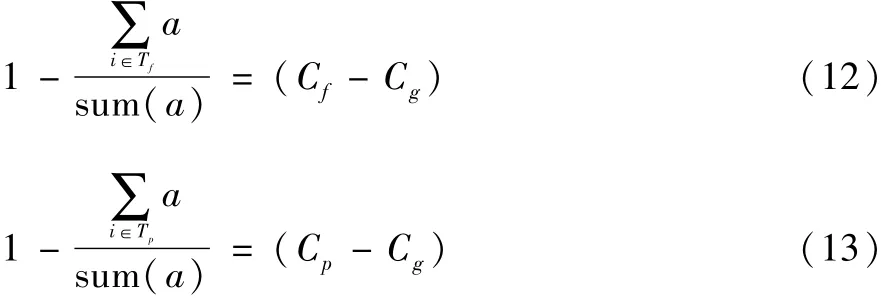
实施分时电价策略不仅要考虑用户的充电电价，同时充电站的利益也不能受损，保证充电站实施分时电价前后的充电电价水平应该大致相当，即充电前后平均电价保持不变。

式中：C为优化前的电动汽车充电电价。

由式（12）～式（14）可知，在已知每时段最优电动汽车充电数量的基础上，可求得峰、平、谷各时段电价Cf、Cp、Cg，根据式（7）计算每时段处于充电状态下的电动汽车数量，进而得到系统最优状态下的负荷曲线。

3．2 电网公司对缩小峰谷差所给予的激励模型

由于充电站制定的充电电价机制，电动汽车用户往往会选择从较高电价的充电时段转移至谷时段进行充电，这一方面用户可以降低充电成本，另一方面也在一定程度上降低了系统的负荷峰谷差，但充电站可能会因为充电负荷的转移而减少了充电站的整体收益，这对于充电站来说是难以接受的。假设电网公司依据充电站优化的电网的负荷峰谷差给予相应的激励来弥补充电站的损失，可以在很大程度上提高充电站实施分时电价机制的积极性。充电站获得激励设置如下：

式中：L0P－V为优化前负荷峰谷差；L1P－V为优化后负荷峰谷差；k3为激励系数。

充电站实施分时电价后，总的售电收益与购电收益之差不能低于优化前的总收益。设优化前后充电站日总收益分别为C*0、C*，为了保证实施分时电价后，充电站的基本收益不受损，则有约束条件：C*＋RP－V≥C*0。

4 算例分析

4．1 参数设置

假设小区配电变压器容量为Ptrans＝1600 kVA，小区内电动汽车保有量是100辆，电动汽车的电池容量均为SB＝32 kW·h，耗电量为每行驶100 km的耗电为15 kW，充电功率Pc＝5 kW，采用恒功率充电方式。本文记录居民小区全天96个时段负荷数据，时间间隔为15 min，绘制了常规负荷曲线。实行峰谷电价之前，小区内电动汽车充电费用为1元／（kW·h），电网公司依据负荷峰谷差的变化所设置的激励系数为1.5元／（kW·h）。充电站向电网购电电费采用工业电价，电价及时段划分见表1。

表1 分时电价及时段划分表

4．2 仿真过程及分析

本文采用Matlab R2014a对电动汽车的充电负荷进行仿真实验，分别在无序充电和有序充电两种模式下对电动汽车安排充电。无序充电是指电动汽车在无引导机制下的随机充电，有序充电是指电动汽车按照充电站所提出的控制策略安排充电，通过仿真结果分析优化前后的系统负荷情况，如图2所示，仿真结果体现了电动汽车在无序充电和有序充电情况下的负荷情况。

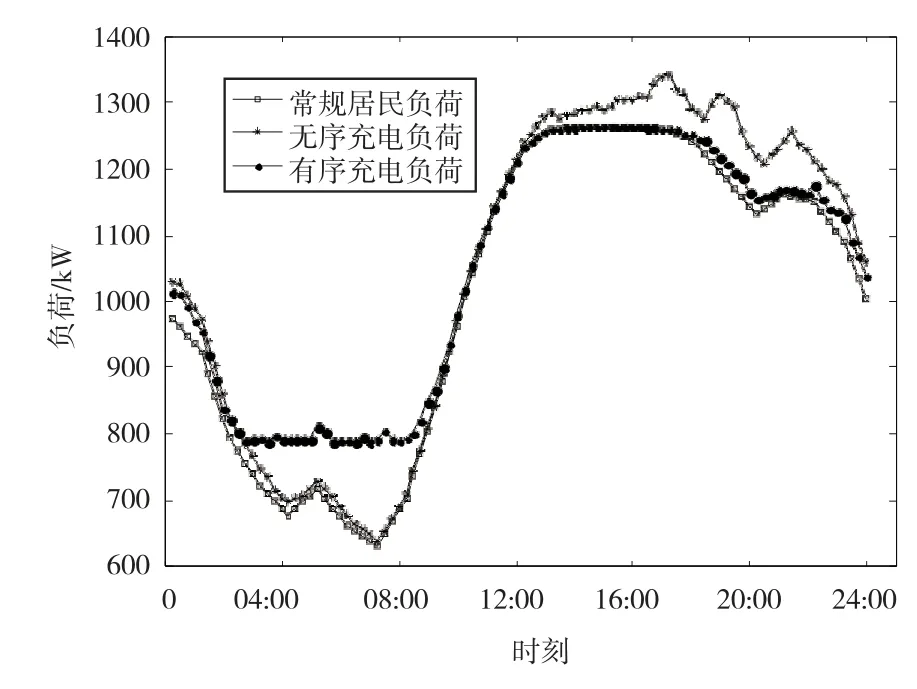
图2 有序充电和无序充电负荷曲线

从图2可知，在充电站实施分时电价前后，负荷峰值有明显的降低，负荷谷值得到了有效填充，既降低了充电站的优化控制和规划难度，同时提高了系统运行的经济性和安全性。

无序充电情况下汽车数量分布如图3所示。

图3 无序充电电动汽车数量分布

从图3可知，在无序充电情况下，大部分用户选择即时充电的方式，充电负荷主要集中在常规用电高峰期，造成充电负荷与基本负荷的叠加，这势必会影响系统运行的稳定性。

有序充电时汽车随时段分布情况如图4所示。

从图4可知，在有序充电情况下，用户由于对分时电价的响应，电动汽车主要集中在夜间时段进行充电，这样不仅可以降低用户充电费用，同时也转移了电网的负荷压力。

优化前后配电变压器负荷变化情况见表2。

图4 有序充电电动汽车数量分布

从表2可知，通过对规模化入网的电动汽车充电进行有序充电，配电变压器峰荷较优化前仅仅减小了3.82%，配电变压器谷荷较优化前增加了22.3%，峰谷差较优化前减小了28.33%，说明在一定程度上实现了配电变压器的削峰填谷，所需充电的电动汽车较多转移至谷时段进行充电。

表2 负荷优化前后配电变压器负荷峰谷差及变化率

结合式（12）～式（14）的电动汽车充电数量与电价之间的响应关系，可得出负荷优化前后各时段电价及电价变化率，见表3。

表3 负荷优化前后各时段充电电价及变化率

从表3可知，对于电动汽车充电优化后，峰时段电价较优化前显著增加了31.98%，平时段较优化前增加了27.15%，谷时段较优化前降低了59.13%，且谷时段下降较为明显。

表4列出了两种模式下负荷峰谷差的分布和100个电动汽车用户充电成本以及充电站收益的对比。

从表4可知，用户整体充电费用较优化前变化较大，降低了39.18%，极大地降低了用户侧充电成本，对用户侧响应分时电价的响应力度产生了较大的意义；充电站购电总费用较优化前降低了40.64%，虽然充电站整体收益较优化前变化不大，仅增加了3.7%，可是充电站的整体利益得到了较大的提高。因此，通过实施峰谷分时电价，既能降低系统的峰谷差，又能降低电动汽车用户的充电成本，同时也提高了充电站的整体利益，具有可行性。

表4 有序充电前后用户充电成本及充电站成本及收益

5 结束语

本文构建了基于峰谷分时电价用户和充电站及电网同步响应模型。在考虑了电动汽车的充电需求、配电变压器容量约束以及充电站优化前后总收益不受损的前提下，以负荷峰谷差最小为优化目标，采用遗传算法对负荷模型进行求解，得到每时段电动汽车的最优充电计划。同时根据电动汽车充电数量与充电价格的响应模型，求解出充电站的合理定价机制，所提的控制策略对系统安全以及能源节约方面具有显著的促进作用。