双重Stone代数的O理想

赵秀兰，史永杰

（1.黄河科技学院数理部，郑州450063；2.汕头大学理学院，广东 汕头515063）

引言

Ockham代数是格与序代数理论的一个重要领域，它是定义在分配格上的一类序代数［1］。布尔代数、Stone代数、MS代数等是Ockham代数的子代数，Ockham代数的部分研究成果见文献［1-4］。在分配格代数研究领域，利用代数的理想和滤子研究代数的结构及其特征是比较常用的一种方法，特别是利用不同定义、不同结构的理想和滤子来研究代数结构是常用的手段，其中常用的理想和滤子就包括有素理想、核理想、余核滤子、O理想等。例如，文献［5］给出了格的反软理想新概念，证明2个反软理想分别在软集的限制并和“或”运算下仍然是反软理想。文献［6-7］利用滤子讨论了Bl代数的性质。文献［8］利用素理想将代数系统分划为若干块，并用素理想刻画代数同余关系。文献［9-13］在相应的代数类上引入理想与滤子，以核理想与余核滤子为载体刻画相应代数同余结构。O理想就是一类特殊的核理想，是W.H.Vornishz在研究分配格时首次提出的，通过O理想得出了关于分配格性质的若干结论［4］，这极大地丰富了分配格理论。之后许多学者开始研究O理想，杨云在文献［15］中将分配格中的O理想推广到伪补分配格，给出伪补分配格的理想是O理想的判别条件；文献［16］利用了O亮素理想刻画出了几乎分配格的代数结构及其特征。

本文以文献理论为基础，将O理想引入到双重Stone－代数上，综合考虑双重Stone代数的运算特征，讨论双重Stone代数上O理想和核理想的关系，从而刻画双重Stone代数的内部代数结构。

1 预备知识

定义1［1］一个伪补代数（简称p代数）是一个分配格（L；∨，∧），它具有一个最小元0及一个映射*：L→L，使得

一个伪补代数（L；∧，∨，*，0，1），如果运算*满足条件：∀x∈L，x*∨x**＝1，则称（L；∧，∨，*，0，1）为Stone代数。

对偶地，附加的一元运算＋：L→L，使得x＋＝min｛y且运算＋满足条件∀x∈L，x＋∧x＋＋＝0，则称（L；∨，∧，＋）是对偶Stone代数。

定义2［1］设（L；∧，∨，0，1）是一个有界分配格，其上赋予两个一元运算*，＋，并且（L；∨，∧，*）是Stone代数，（L；∨，∧，＋）是对偶Stone代数，则称（L；∨，∧，*，＋）是一个双重Stone代数。

引理1［1，17］设（L；∨，∧，*，＋）是一个双重Stone代数，任意的x，y∈L，则有：

定义3［1］设（L；∨，∧，*，＋）是一个双重Stone代数，θ是L的格同余关系，若（x，y）∈θ⇒（x*，y*）∈θ，（x＋，y＋）∈θ，则称θ是L的同余关系，符号Con（L）表示L的全体同余关系构成的集合。

定义4［1］设（L；∧，∨）是一个格，I是格L的子格，若x，y∈L，y≤x∈I总有y∈I，则称子格I是格L的理想。对偶地，F是格L的子格，若x，y∈L，y≥x∈F总有y∈F，则称子格F是格L的滤子。

定义5［1］设（L；∨，∧，*，＋，0，1）是一个双重Stone代数，对于L的理想I，若存在L的一个同余关系φ，使得I＝Ker（φ），其中Ker（φ）＝｛x∈L x≡0（φ）｝，则称理想I为L的核理想。对于L的滤子F，若存在L的一个同余关系φ，使得F＝CoKer（φ），其中，则称滤子F为L的余核滤子。

为便于阐述，假定L是双重Stone代数，a，b∈L，F⊆L，符号θ（a，b）和θlat（a，b）分别表示包含a，b的最小同余与最小格同余（即由a，b所生成的主同余和格主同余）；用θ（F）和θlat（F）分别表示包含F的最小同余与最小格同余（即由F所生成的主同余和格主同余）。

定义6［14］设（L；∨，∧，*，＋，0，1）是一个双重Stone代数，I是L的一个理想，若存在L的一个滤子F，使得I＝Ker（θ（F）），则称I是L的一个O理想。

引理2［9］设（L；∨，∧，*，＋，0，1）是一个双重Stone代数，I是L的理想，则I是核理想的充要条件是（a∈L）a∈I⇒a**∈I。

引理3设（L；∨，∧，*，＋，0，1）是一个双重Stone代数，F是L的滤子，则F是余核滤子的充要条件是（a∈L）a∈F⇒a＋＋∈F。

证明

证明充分性。若F是L的余核滤子，则存在φ∈Con（L），使得F＝CoKer（φ）。设a∈F，故a≡1（φ），从而a＋＋≡1（φ），所以a＋＋∈F。

证明必要性。设a∈L，a∈F蕴涵a＋＋∈I。在L上定义一个等价关系RF如下：

（x，y）∈RF⇔（∃i∈F）x∧i＝y∧i易得RF是一个格同余。

证明RF∈Con（L）。设（x，y）∈RF，则存在i∈F，使得x∧i＝y∧i，从而有x*∨i*＝y*∨i*，x＋∨

i＋＝y＋∨i＋，i**∧（x*∨i*）＝i**∧（y*∨i*），i＋＋∨

（x＋∧i＋）＝i＋＋∨（y＋∧i＋）。由引理1知，i*∧i**＝1，i＋∧i＋＋＝1，根据双重Stone代数运算的分配性可得i**∧x*＝i**∧y*，i＋＋∧x＋＝i＋＋∧y＋。在双重Stone代数中，由引理1知任意的x∈L，x＋＋≤x≤x**，所以可得i＋＋∧x*＝i＋＋∧y*，由题设知i＋＋∈F，所以（x*，y*）∈RF，（x＋，y＋）∈RF，因此RF∈ConL。

证明F＝CoKer（RF）。设x∈CoKer（RF），则（x，1）∈RF，故存在i∈F，并有x∧i＝i，从而x≥i∈F，因此x∈F，从而CoKer（RF）⊆F。再设i∈F，因为i＋＋∈F，且由引理1知i≥i＋＋，故i∈CoKer（RF），因此F⊆CoKer RF，所以F＝CoKer（RF）。

设（L；∨，∧，*，＋，0，1）是一个双重Stone代数，I是L的核理想，定义FI＝｛x∈L（∃a∈I）x≥a*｝，显然，FI是L的滤子，现有如下结论。

引理4［9］设（L；∨，∧，*，＋，0，1）是一个双重Stone代数，I是L的核理想，则

θ（I）＝θlat（I）∨θlat（FI）

引理5［9］设（L；∨，∧，*，＋，0，1）是一个双重Stone代数，I是L的核理想，则：

（x，y）∈θ（I）⇔（∃a，b∈I）（x∨a）∧b*＝

（y∨a）∧b*

引理6［9］设（L；∨，∧，*，＋，0，1）是一个双重Stone代数，I是L的核理想，x，y∈L，则下列命题等价：

（1）（x，y）∈θ（I）；

（2）（∃a∈I）x∨a＝y∨a；

（3）（∃a，b∈I）（x∨a）∧b*＝（y∨a）∧b*。

设（L；∨，∧，*，＋，0，1）是一个双重Stone代数，F是L的余核滤子，定义IF＝｛x∈L（∃a∈F）x≤a＋｝，显然，IF是L的理想，现有如下结论。

引理7设（L；∨，∧，*，＋，0，1）是一个双重Stone代数，F是L的余核滤子，则θ（F）＝θlat（F）∨θlat（IF）。

证明 设a，b∈L且a≤b，由文献［2］与定理1知：

θ（a，b）＝θlat（a，b）∨θlat（b*，a*）∨

θlat（a**，b**）∨θlat（b＋，a＋）∨θlat（a＋＋，b＋＋）

由引理3知，a＋＋，b＋＋∈F，又因a＋＋≤a≤a**，a＋≥a*，b＋＋≤b≤b**，b＋≥b*，故：

a，b，a＋＋，b＋＋，a**，b**∈F

a*，b*，a＋，b＋∈IF

故θlat（a，b），θlat（a**，b**），θlat（a＋＋，b＋＋）≤θlat（F），θlat（b*，a*），θlat（b＋，a＋）≤θlat（IF），于是θ（a，b）≤θlat（F）∨θlat（IF）。

又由文献［1］知，θ（F）＝∨｛θ（a，b）a，b∈F｝，所以θ（F）≤θlat（F）∨θlat（IF）。

再因θlat（F）≤θ（F）。设a，b∈IF且a≤b，由IF的定义知，存在c∈I，使得c＋≥b≥a。由于（c，1）∈θ（F），故（c＋，0）∈θ（F），从而 有（a∧c＋，a∧0）∈θ（F），（b∧c＋，b∧0）∈θ（F），于是（a，0）∈θ（F），（b，0）∈θ（F），所以（a，b）∈θ（F）。

为了探讨双重Stone代数核理想与O理想的关系，需要下面的引理。

引理8设（L；∨，∧，*，＋，0，1）是一个双重Stone代数，F是L的余核滤子，则：

（x，y）∈θ（F）⇔（∃a，b∈F）（x∧a）∨b＋＝

（y∧a）∨b＋

证明 定义L上一个等价关系φ为：

（∃a，b∈F）（x∧a）∨b＋＝（y∧a）∨b＋从中易见φ是一个格同余关系。

下证φ∈Con（L）。

设（x，y）∈φ，则（∃a，b∈F）（x∧a）∨b＋＝（y∧a）∨b＋，故：（x*∨a*）∧b＋*＝（y*∨a*）∧b＋*，（x＋∨a＋）∧b＋＋＝（y＋∨a＋）∧b＋＋。根据运算的分配性有：

（x*∧b＋*）∨（a*∧b＋*）＝（y*∧b＋*）∨（a*∧b＋*）（x＋∧b＋＋）∨（a＋∧b＋＋）＝（x＋∧b＋＋）∨（a＋∧b＋＋）

由引理1知，a＋≥a*，b＋*＝b＋＋，于是由（x*∧b＋*）∨（a*∧b＋*）＝（y*∧b＋*）∨（a*∧b＋*），可得（x*∧b＋*）∨a＋＝（y*∧b＋*）∨a＋，又因b＋*＝b＋＋，而a＋∧b＋＋＝（a∨b＋）＋，故a∨b＋≥a∈F，又因F是L的余核滤子，由引理3知，b＋＋∈F，所以（x*，y*），（x＋，y＋）∈φ，因此φ∈Con（L）。

再证φ＝θ（F）。

设（x，y）∈φ，则存在a，b∈F，使得（x∧a）∨b＋＝（y∧a）∨b＋。因为（a，1）∈θlat（F），（b＋，0）∈θlat（IF），所以（x，x∧a）∈θlat（F），（（x∧a）∨b＋，x∧a）∈θlat（IF），因此（x，（x∧a）∨b＋）∈θlat（F）∨θlat（IF）。同理可得，（y，（y∧a）∨b＋）∈θlat（F）∨θlat（IF），所以（x，y）∈θlat（F）∨θlat（IF），即φ∈θlat（F）∨θlat（IF），由引理7知，φ≤θ（F）。

另设（x，y）∈θlat（F）∨θlat（IF），则存在x＝x0，x1，．．．，xn－1＝y且（xi，xi＋1）∈θlat（F）或者（xi，xi＋1）∈

θlat（IF）（i＝0，1，2，．．．，n－2）。

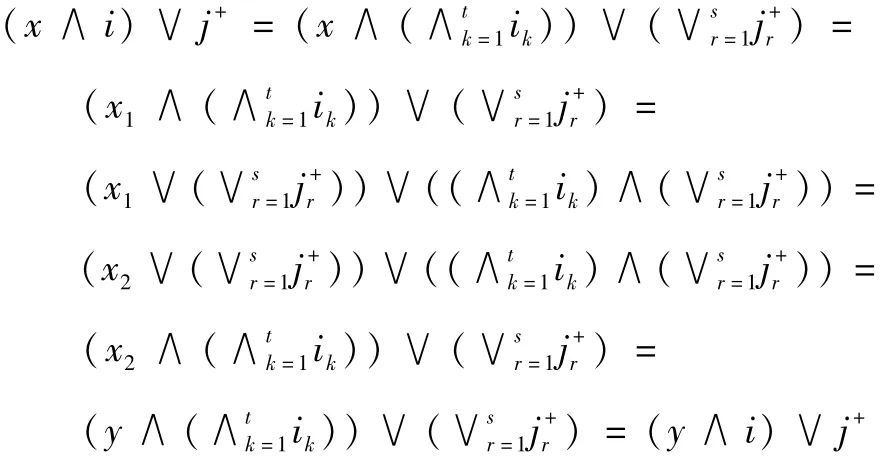
因此（x，y）∈φ，故θ（F）≤φ。定理得证。

引理9设（L；∨，∧，*，＋，0，1）是一个双重Stone代数，F是L的余核滤子，x，y∈L，则下列命题等价：

（1）（x，y）∈θ（F）；

（2）（∃a∈F）x∧a＝y∧a；

（3）（∃a，b∈F）（x∧a）∨b＋＝（y∧a）∨b＋。

证明 易得，（2）⇒（3）。

由引理8得，（1）⇔（3）。

下证（3）⇒（2）。设存在a，b∈F，使得（x∧a）∨b＋＝（y∧a）∨b＋。因此（（x∧a）∨b＋）∧b＋＋＝（（y∧a）∨b＋）∧b＋＋，根据Stone代数运算的分配性及运算性质b＋∧b＋＋＝0，所以有：x∧a∧b＋＋＝y∧a∧b＋＋。又由引理3知，b＋＋∈F，又因a∈F，故a∧b＋＋∈F，所以（2）成立。

以上述引理为理论基础来探讨双重Stone代数核理想与O理想的关系。由核理想与O理想的定义知，O理想一定是核理想。那么，核理想是否一定是O理想呢？下面的定理4对此给出了答案。

2 主要结论

设（L；∨，∧，*，＋，0，1）是一个双重Stone代数，a∈L，定义有下列性质。

定理1设（L；∨，∧，*，＋，0，1）是一个双重Stone代数，I是L的一个核理想，x∈L，令σ（I）＝｛x∈，则σ（I）是L的一个O理想。

证明 由于任意的x∈L，有x≤1，且0*＝1，故0∈σ（I）。

设x，y∈σ（I），即（x*］∨I＝L，（y*］∨I＝L。下证x∧y，x∨y∈σ（I）。根据引理1可得：

（（x∧y）*］∨I＝（x*∨y*］∨I＝

（（x*］∨I）∨（（y*］∨I）＝L

（（x∨y）*］∨I＝（x*∧y*］∨I＝

（（x*］∨I）∧（（y*］∨I）＝L

从而有x∧y，x∨y∈σ（I）。

再设y∈L，x∈σ（I）且y≤x，由双重Stone代数的运算性质得y*≥x*，故（y*］∨I≥（x*］∨I＝L，所以（y*］∨I＝L，所以y∈σ（I），故得σ（I）是L的一个理想。

下证σ（I）是L的一个O理想。

令F＝CoKer（θ（I）），下证σ（I）＝Ker（θ（F））。

先证F是L的一个滤子。

设x∈F，y≥x，则（x，1）∈θ（I），由引理4知，存在i∈I，有x∨i＝1∨i＝1，从而y∨（x∨i）＝y∨1∨i，则y∨i＝1∨i，因此（y，1）∈θ（I），即y∈CoKer（θ（I）），于是y∈F，所以F是L的一个滤子。

再证F是L的一个余核滤子。

令x∈F，则（x，1）∈θ（I），由同余关系的定义以及双重Stone代数的运算性质引理1可得（x＋＋，1）∈θ（I），因此x＋＋∈F，由引理3知，F是L的一个余核滤子。

下证σ（I）＝Ker（θ（F））。

设x∈σ（I），则（x*］∨I＝L，从而存在a∈（x*］，b∈I，使得a∨b＝1。又因b∨b＝0∨b＝b，故（b，0）∈θ（I）。因此（a∨b，a∨0）∈θ（I），即（a，1）∈θ（I），故a∈F。又因a∈（x*］，则a∧x＝0，于是a∧x＝0∧a＝0。

又因a∈F，又由引理9知，（x，0）∈θ（F），故x∈Kerθ（F），所以σ（I）⊆Ker（θ（F））。

另一方面，设x∈Ker（θ（F）），即（x，0）∈θ（F），由引理9知，存在j∈F，使得x∧j＝0∧j＝0，从而j∈（x*］。

又因F＝CoKer（θ（I）），故（j，1）∈θ（I），由引理6知，存在i∈I，使得j∨i＝1∨i＝1，因此（x*］∨I＝L，即x∈σ（I），所以Ker（θ（F））⊆σ（I）。

综上得σ（I）＝Ker（θ（F）），所以σ（I）是L的一个O理想。

为了论证双重Stone代数上核理想和O理想的关系，需要下面定理2与定理3。

定理2设（L；∨，∧，*，＋，0，1）是一个双重Stone代数，I是L的核理想，则I＝Ker（θ（I））。

证明 先证Ker（θ（I））为L的核理想。

设x，y∈Ker（θ（I）），下 证x∧y，x∨y∈Ker（θ（I））。

由于（x，0）∈θ（I），（y，0）∈θ（I），由同余关系的定义得（x∧y，0）∈θ（I），（x∨y，0）∈θ（I），从而x∧y，x∨y∈Ker（θ（I））。令x∈Ker（θ（I）），y≤x，则（x，0）∈θ（I），从而（x∧y，0∧y）＝（y，0）∈θ（I），故y∈Ker（θ（I））。所以Ker（θ（I））为L的理想。

设x∈Ker（θ（I）），则（x，0）∈θ（I），故（x**，0）∈θ（I），所 以x**∈Ker（θ（I）），由 引 理2知，Ker（θ（I））为L的核理想。

下证I＝Kerθ（I）。设x∈Ker（θ（I）），则（x，0）∈θ（I）。由引理6知，存在i∈I，使得x∨i＝i，从而x≤i，所以x∈I，因此Ker（θ（I））⊆I。

另一方面，若x∈I，由于I是L的核理想，由引理2知，x**∈I。又由引理1知x≤x**，故x∨x**＝0∨x**＝x**，所以x∈Ker（θ（I）），即I⊆Ker（θ（I）），所以I＝Ker（θ（I））。

设（L；∨，∧，*，＋，0，1）是一个双重Stone代数，I是L的核理想，定义显然，FI是L的滤子，现有如下结论。

定理3θ（I）＝θ（FI）。

证明

先证FI为L的余核滤子。设x∈FI，则存在a∈I，使得x≥a*，从而x＋＋≥a*＋＋。由引理1知，a*＋＝a**，因此a*＋＋＝a**＋＝a***＝a*，故x＋＋∈FI，所以由引理3知，FI为L的余核滤子。

设（x，y）∈θ（I），由引理6得，存在i∈I，使得x∨i＝y∨i，又因i≤i**，故x∨i**＝y∨i**，所以i*∧（x∨i**）＝i*∧（y∨i**）。再因i*∧i**＝0，因此x∧i*＝y∧i*。又因i*∈FI，所以由引理9知，（x，y）∈θ（FI）。因此，θ（I）⊆θ（FI）。

另一方面，设（x，y）∈θ（FI），由引理9得，存在j∈FI，使得x∧j＝y∧j。又由j∈FI，则存在a∈I，使得j≥a*，于是x∧a*＝y∧a*，所以（x∧a*）∨a**＝（y∧a*）∨a**。由引理1知，a*∨a**＝1，从而x∨a**＝y∨a**。又因I是L的核理想，且a∈I，故由引理2得a**∈I，所以（x，y）∈θ（I），因此θ（FI）⊆θ（I）。

综上可得，θ（I）＝θ（FI）。

由定理2和定理3，可得双重Stone代数上O理想判别定理。

定理4设（L；∨，∧，*，＋，0，1）是一个双重Stone代数，I是L的核理想当且仅当I是L的O理想。

证明

必要性证明。由核理想和O理想的定义即得。

充分性证明。由定理2和定理3知，I＝Ker（θ（I））＝Ker（θ（FI）），且FI为L的余核滤子，由O理想的定义得I是L的核理想，则I是L的O理想。

3 小结

本文提出了双重Stone代数的O理想的概念，借助O理想与核理想的关系，利用双重Stone代数的核理想与余核滤子同余关系的表达式，给出了双重Stone代数的理想成为O理想的充要条件，这些结论丰富了分配格理论，为其它分配格代数类O理想性质的研究提供了方法。