个体观测次数与协变量个数都趋于无穷的二值数据GEE估计的渐近性质
孙 晗,尹长明,靳永涛
(广西大学数学与信息科学学院,南宁530004)
引言
广义线性模型(Generalized Linear Model,GLM)最早被Nelder和Wedderburn[1]于1972年所引进,用于解决因变量y取离散值的情况。而广义估计方程(Generalized Estimation Equation,GEE)是Liang和Zeger[2]在1986年的一篇具有开创性意义的文章中引入的,作为对广义线性模型相关数据的有用扩展,主要用于分析纵向数据(Longitudinal Data))或集团数据(Cluster Data)。而纵向数据一直是近些年来被研究的热点之一[3]。在应用中,广义估计方程被广泛应用于生物统计、临床试验、车险定价及理赔等领域。张敏等[4]在高血压研究案例当中,以高血压的四类并发症拟合四个常数项,构建广义估计方程,用以计算各并发症在基线水平上的发生概率。Wu等[5]通过收集中国高速公路出口坡道的四年碰撞数据来进行建模,将GEE与传统的GLM进行比较,发现前者可以很好地适用于碰撞频率数据。李静等[6]通过采用GEE方法建立了不同孕周的体重常模。康萌萌和刘素春[7]将GEE应用到车险定价中,与GLM相比,得到的变量更准确。除此之外,GLM和GEE不再仅限于二值数据,在多分类问题中业已广泛应用,详见文献[8-12]。
Wang[13]证明了在个体观测次数有限的情况下经典Logit广义估计方程估计的渐近性质。而随着时代的发展,对个体观测的次数会越来越多,甚至趋于无穷。因此,本文将观测次数由有限推广到了无限,在相近的条件下证明了经典Logit广义估计方程估计的渐近性质。
1 模型介绍
设在试验中对第i个个体的第j次观测,得到二进制响应变量Yij和pn维协变量Xij,其中i=1,…,n;j=1,…,m。对于来自不同个体的观测值,假设其相互独立,而来自相同个体的观测值则认为是相关的,但相关系数未知。令Yi=(Yi1,…,Yim)T表示第i个个体的响应变量,并且Xi=(Xi1,…,Xim)T为m×pn协变量矩阵。假设Ε(Yij,其中h的反函数g为联系函数(Link Function)。对于经典Logit模型来说,联系函数为,βn是一个pn维的参数向量。此外,有:

详细情况可参考文献[14-16]。
在应用中,工作相关矩阵的提出对于分析纵向数据具有重要的意义。但由于受到扰动参数τ的影响,工作相关阵并不容易得到,于是Xie和Yang[17]以及Balan和Schiopu-Kratina[18]假设τ已知,并提出一个非随机的正定矩阵并给出了估计方程:


式中,表示为的真实相关阵且为未知。
Wang[1]定 义 了GEE估 计 量的解,其中R^是工作相关阵,并在一定条件下证明了协变量个数趋于无穷时β^n的渐近性质。本文在其基础上将条件放宽,对个体观测次数也不再设置上限(即趋于无穷),并证明的渐近性质。本文不同位置的C代表不同正常数;对任意矩阵A=(aij),范数为Frobenius范数[13],即:

2 主要结果
为了后文定理叙述的简洁,引入以下假设条件[13]:

(A2)未知参数βn属于紧子集B⊆Rpn,真实参数值βn0是集合B的内点,且∃c1,c2>0,使得c1≤λmin(Ai(βn0))≤λmax(Ai(βn0))≤c2,其中λmin,λmax分别表示矩阵的最小、最大特征值;
(A3)∃c3,c4>0,满足:
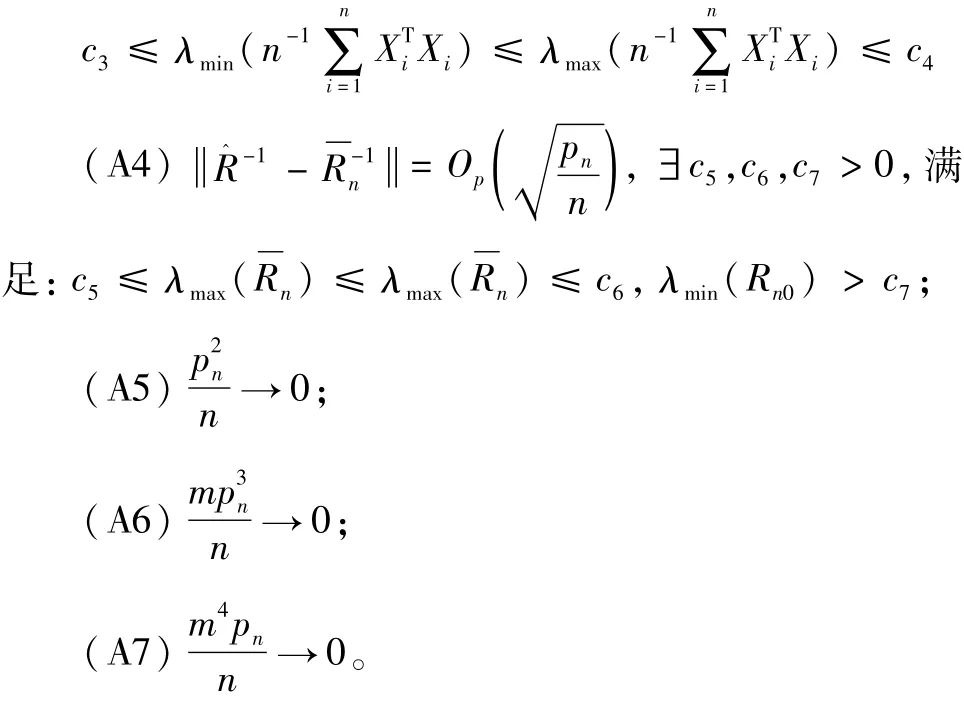
定理1关于渐近存在性和相合性。对于经典Logit模型,假设(A1)~(A7)成立,则方程Sn(βn)=0存在一个根β^n,且β^
n满足:
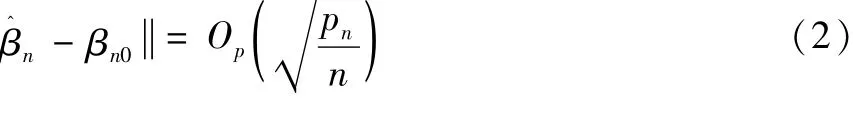
定理2关于渐近正态性。对于经典Logit模型,假设(A1)-(A7)成立,则,有:
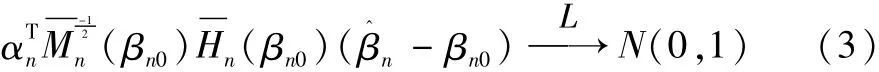

3 定理的证明
关于定理的证明需要用到以下引理。
引理1式中:


ej为第j个元素、为1,其他均为0的m维列向量。引理2假设条件(A1)~(A5)成立,则:

引理3假设条件(A1)~(A5)成立,则∀Δ>0,bn∈Rpn,有:

引理4假设条件(A1)~(A4)以及(A6)成立,则∀Δ>0,bn∈Rpn,有:

引理5假设条件(A1)~(A5)成立,则∀Δ>0,bn∈Rpn,有:

引理6设G是Rn中的有界开集,记G的闭包和边界分别是,∂G。若函数F→Rn是连续的,并且对某个x0∈G和所有的x∈∂G有(x-x0)TF(x)≤0,则F(x)=0有一个根在中。参见文献[19]。
引理7假设条件(A1)~(A5)成立,则∀αn∈Rpn,αn=1,有:

定
?理1的证明 由微分中值定理和引理1,可得:

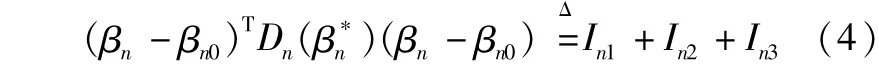
式中,β*n在βn和βn0连线内。
首先估计In1。由引理2及(A7)可得:

其次估计In2,对求期望,即:
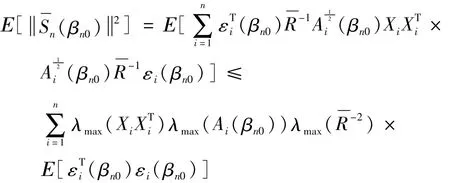
由(A1)-(A4)可知:

所以有:
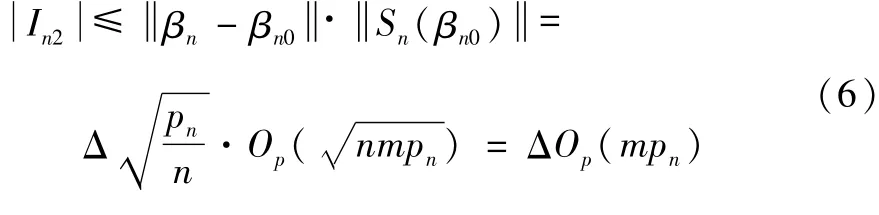
对于In3有:
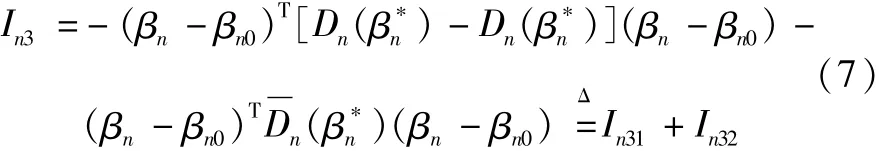
由引理3和(A6)可得:

由(A2)-(A4)可得:
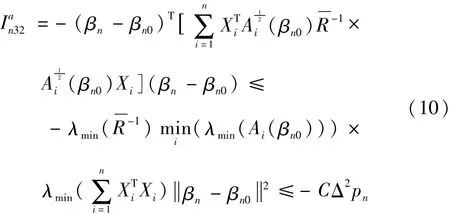
而由引理4、引理5以及(A5)、(A6)可得:

由式(7)~式(12)可知In3≤-CΔ2pn,再由式(5)、式(6)可知:


最后,根据引理6可知式(5)成立,于是定理1得证。
定理2的证明 由定理1可知,Sn(β^n)=0。根据拉格朗日中值定理可得:

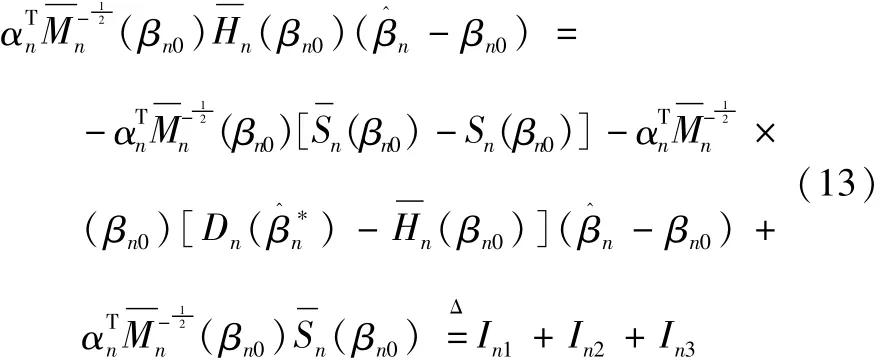
由(A2)、(A4)和式(1)可知,对于∀bn∈Rpn且bn≠0,
有:

则根据Rayleigh-Rize定理以及(A3)可知:

首先证明In1=op(1)。由Cauchy-Schwarz不等式、引理1、
式(14)以及(A5)可得:

其次证明In2=op(1),由于
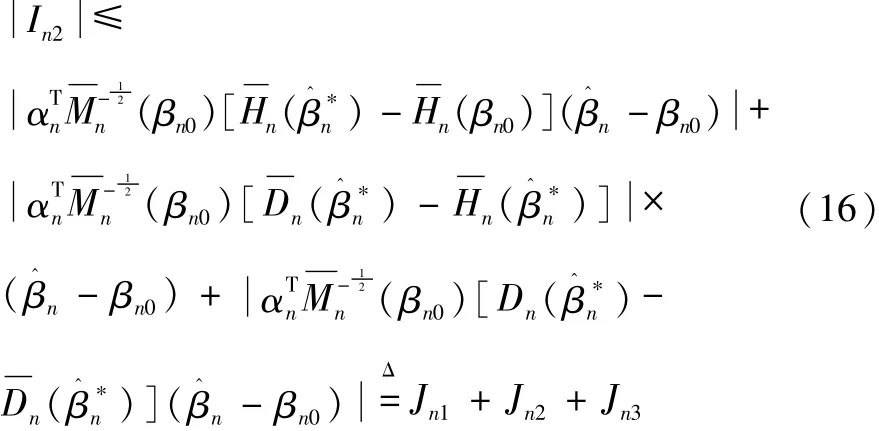
故需依次证明Jni=op(1),i=1,2,3,首先证明Jn1=op(1)。

以及(A5)可得:
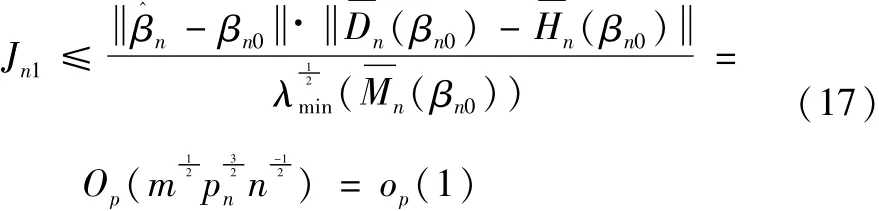
同理,运用引理3、引理4,式(3)以及(A3)、(A6)可得:

由式(15)-(19)可得,In1=In2=op(1)。最后根据引理7,式(13)和Slutsky定理可知式(3)成立,即定理2得证。
4 实例分析
例1对于经典Logistic回归模型产生的纵向数据:

魏强强[20]通过随机模拟,产生了个体观测数n为20,每个个体观测值m为15次,且协变量维数pn为4的数据,根据Newton-Raphson迭代法选取初值βn0=经过15次迭代收敛到β^n=,偏差较小。由此可得,当条件(A1)~(A7)成立时,有:

例2为了研究某种新型的治疗精神抑郁病药物是否有更好的疗效,某研究中心将其与标准药物进行对比,做了如下试验。该试验是由340位病人共同参与,并根据各个体抑郁症的严重程度进行划分,且每组分别被随机地指定服用新型药或标准药,分别记录个体接受治疗后在1、2和4周的情况,按精神抑郁的程度,各个体被划分为正常(N)或异常(A),具体数据见表1,数据来自Biometric Society。

表1 抑郁的三次响应对治疗和抑郁严重程度的交叉划分
表1给出了基于独立工作关联的GEE估计。而对于该数据来说,GEE估计等于通过经典Logit模型,将3×340=1020个观测值当做非独立的观测,进而得到回归结果。通过运算分析可以得出抑郁严重程度、药物治疗方式以及时间都对正常响应具有实质影响。最初,两种药物的药效相似,均随着时间而增长,但新型药物的药效增长幅度更大。随着观测次数(周数)的增多,所得到的效果也会更加稳定。详细请参考文献[21]。由此可见,观测次数的适当增加,可使得试验结果更加理想。

