基于Matlab的六自由度工业机器人运动学逆解分析及仿真

丁志鹏，江 明，游 玮，梁兆东，冯海生，葛景国

（1.安徽工程大学电气工程学院，安徽 芜湖241000；2.埃夫特智能装备股份有限公司，安徽 芜湖241000）

引言

近年来，工业机器人发展迅猛，各行各业中对工业机器人的需求不仅从数量上大幅度提高，对其性能要求也越来越高，必须不断提高对机器人的控制精度，才能满足企业对于制造能力和效率的要求，所以有必要对工业机器人的运动学进行研究。机械臂作为强耦合性、高复杂性的机械系统，只有准确分析其末端执行器在空间中的位置和姿态，才能让其完成预想的轨迹运动［1］。

机器人运动过程中，受到生产现场实际条件约束，如操作空间中存在奇异点，影响其实际运动。传统解析法求解逆运动学方法的计算量大，易受非线性影响，存在无解或者少解的情况，因此拟采用几何法来求解逆运动方程，提高求逆解运算速度，避免奇异点对逆运动方程的解造成不良影响。

目前，国内许多学者已在寻求更好的运动学求逆解方法上做了不少研究。四川大学韩兴国［2］提出一种基于动态模糊神经网络进行求逆解的方法，建立了运动学逆解预测模型；上海交通大学朱晓龙［3］根据其提出的末端姿态描述，得到一种对五自由度机械臂运动方程求逆的几何方法。

Matlab环境下的机器人仿真功能十分强大，本文基于此建立仿真模型，模拟机器人在操作空间中的轨迹运动，能为研究机械臂运动过程中的平稳性提供有力依据。

1 机器人结构及坐标系的建立

ER7B-C10机器人是一款埃夫特公司生产的可用于装配和物料搬运等的多功能六自由度工业机器人，其本体结构如图1所示。进行机器人正运动学分析之前，首先分析其机械臂结构，这对于关节链中如何在每一个连杆上建立合适的坐标系十分重要。D-H方法由Denavit和Hartenberg于1955年提出，其参数使用连杆参数来描述机构运动关系［4］。按照D-H规则来定义连杆坐标系，对求解机器人运动学能带来较大的便利。D-H方法具体建立过程为：

图1 ER7B-C10机器人本体结构

步骤1：从低序到高序来寻找定义关节轴，将轴的方向设为z0，…，zn－1。

步骤2：选择坐标系0，将原点定于轴z0上，并选择x0和y0构成右手系。

步骤3：将原点Oi定位于轴zi、轴zi－1和zi公垂线的交点。对于转动关节，如果轴zi和zi－1平行，则建立原点使得偏置为0；对于移动关节，则将原点建立在关节延伸范围的某一个参考点上。

步骤4：将xi轴建立在轴zi－1和zi公垂线上，其方向由关节i指向关节i＋1。

步骤5：根据右手定则，由xi轴和zi轴的方向确定yi的方向。

步骤6：坐标系n的建立由关节n的类型决定，对于转动关节，则按照zn－1来设置zn；对于移动关节，则任意选择zn的方向。按照上述方法建立坐标系如图2所示。

图2 关节坐标系位置示意图

臂结构运动学分析中，D-H法巧妙地运用4个基本参数αi、ai、di、θi来描述机械臂中的连杆，其中αi和ai描述了关节i和关节i－1之间的关于z轴的结构关系，而di和θi则描述了两个关节之间关于x轴的位置关系。图中Li表示机器人各关节间的连杆偏移量参数，ER7BC10机器人的D-H参数见表1。

表1 机器人D-H参数

2 运动学方程的建立

2．1 正运动学方程

建立正运动学的目的是通过各个关节变量的值计算出机械臂末端执行器在笛卡尔空间的位置和姿态，描述末端执行器与基坐标之间关系的齐次坐标变换矩阵可由D-H法得到［5］。根据D-H法定义的规则，坐标系i－1与坐标系i之间的关系可描述为坐标系i沿轴zi－1平移di，并绕轴zi－1旋转θi，之后再沿轴xi平移ai，旋转αi，得到如下齐次变换矩阵：

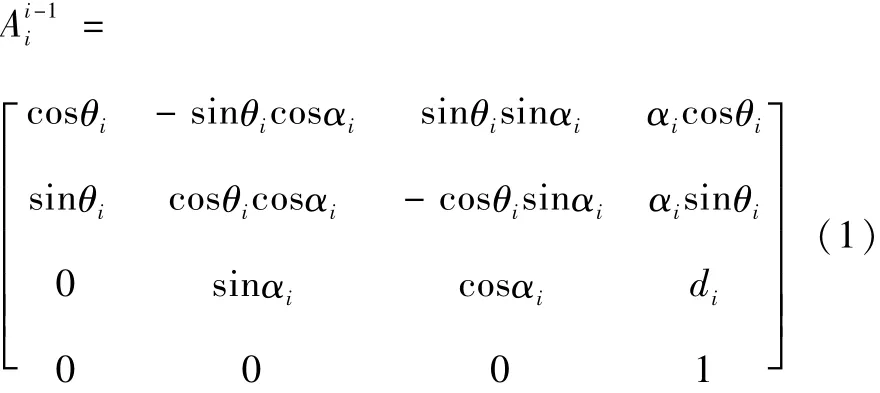
将表1中的参数αi、ai、di、θi带入齐次变换矩阵（1），可得到机械臂中相邻两个关节坐标系之间的变换关系：

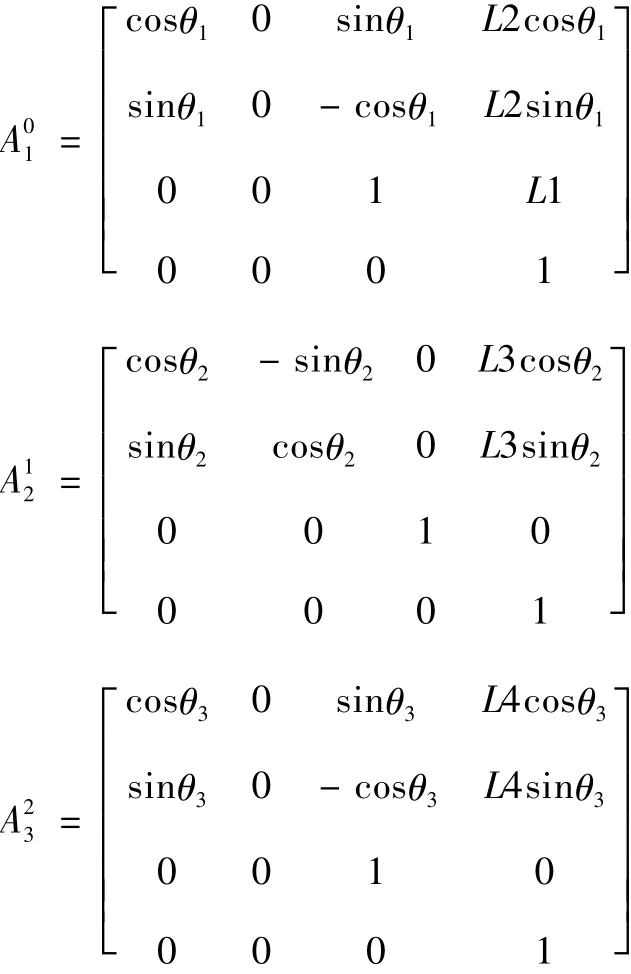
末端执行器与基坐标之间的齐次变换矩阵T06是由机械臂中从低序到高序的所有相邻坐标系之间的变换关系Aii－1依次相乘而得：

T06即为末端执行器的位置和姿态在基坐标系下的表示，该机器人正运动学模型可以被划分为两个部分：（a）机器人手臂部分T03（qA）和机器人手腕（工具）部分

其中：

若机器人末端执行器实际位置和姿态与式（4）中所计算出的结果有偏差，那么说明机器人运动过程并未绝对按照轨迹到达目的点，这可能是受到误差影响，因此需要对机器人在投入使用前进行标定并运用修正误差模型来校正其在操作空间的位姿［7］。

2．2 逆运动学方程

与正运动学相反，逆运动学主要解决的是由机器人末端执行器在操作空间中的位置和姿态来逆向推导出机械臂上各个关节变量的值［8］。逆运功学问题较正运动学问题更为复杂，其原因主要有：（1）计算过程中较多出现非线性方程；（2）计算结果存在多种情况，多解或无穷多解；（3）机器人操作空间存在奇异点导致方程无解或漏解［9］。所以计算逆运动学需要选择正确合适的方法，才能简化其复杂的计算过程。

总的来说，解决机器人逆运动学问题的方法主要有两大类［10］：封闭解和数值解。前者可分为解析法和几何法进行求解，目前引用较为广泛的方法为解析法，但是解析法的缺点是解析中代数较多、求逆复杂、计算量较大，因此本文采用几何法对该逆运动方程进行求解，计算过程中所涉及参数均在图3中标注。

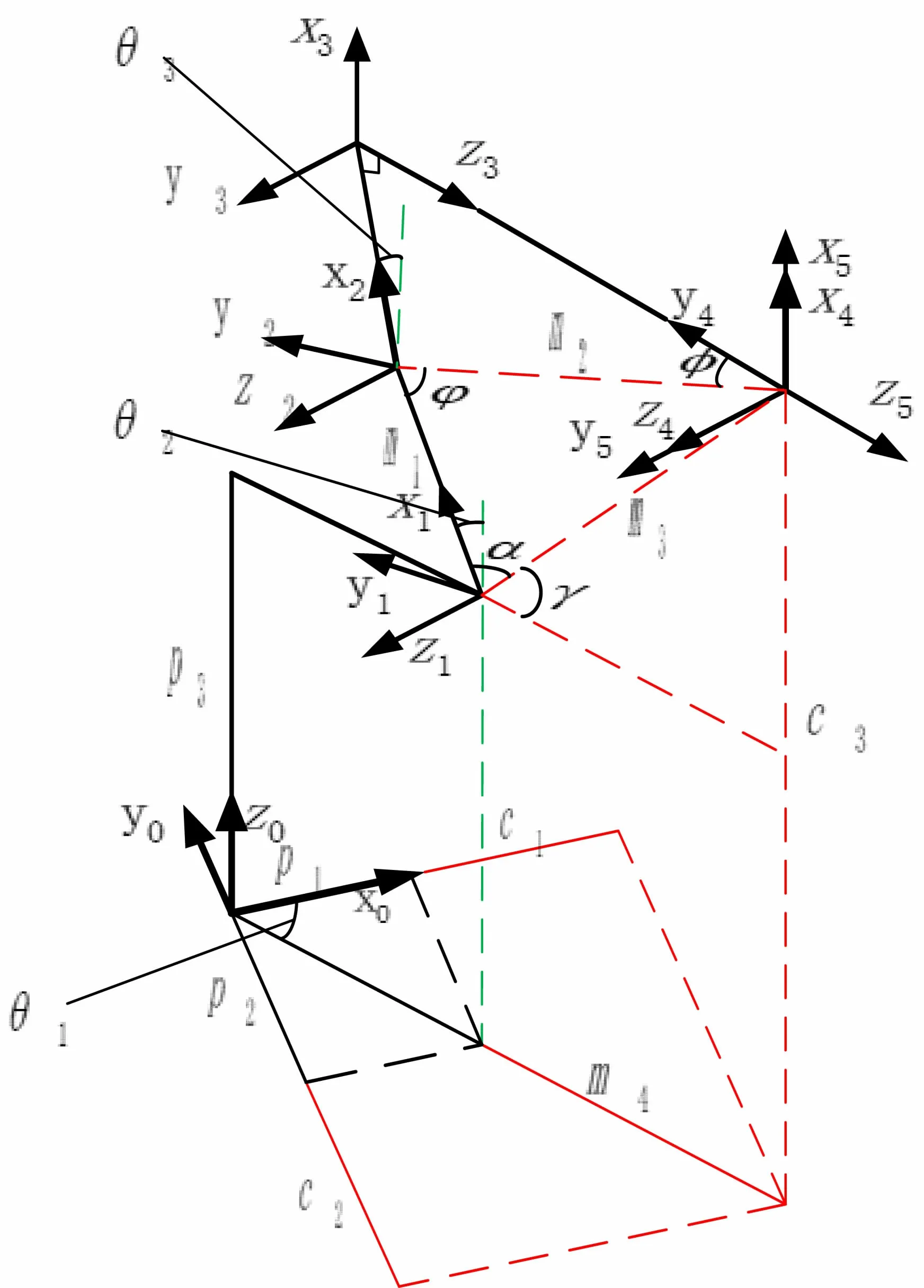
图3 机器人坐标系逆解几何图

先对机器人手臂部分关节变量θ1、θ2、θ3进行求解，再对机器人手腕部分变量θ4、θ5、θ6进行求解，这既可以逐步减少变量、减少计算，又充分利用了前3个关节与位置相关而后3个关节与姿态有关的特性，减少了变量之间相互的影响［11］。cosθ1、cosθ2、cosθ3的值可在关节5于笛卡尔坐标系中的位置关系中求得。

则关节变量θ1有：

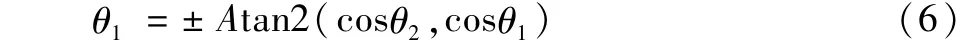
根据图中几何关系，通过相似定理和余弦定理很容易得到：

则关节变量θ3：

同理可以计算出：

则关节变量θ2：

求出前3个关节变量后，将θ1、θ2、θ3作为已知量带入到T03中，由T06右乘T03的逆矩阵后得到球形手腕齐次矩阵T36

T36中各元素为计算后常数值，仅与3个关节变量θ4、θ5、θ6有关，求法如下：

根据式（4）中关于手腕部分正运动方程的表达式可以求得T36内包含θ4、θ5、θ6的关系式，带入A34、A45、A56中进行推导可求得：

3 基于Matlab的运动学仿真

3．1 机械臂模型的建立

Matlab是Mathworks公司开发的功能强大的工程计算应用软件，配备了强大的矩阵计算能力，其软件中的Robotics Toolbox工具箱不仅可以实现对机器人运动学的可视化仿真，还可以对手工计算正逆解结果进行验证［12］。

通过调用建立连杆函数指令Link将表1中D-H参数输入到仿真机械臂模型中，再通过SerialLink函数建立模型，如图4所示，模型与机器人实物大小比例为1∶100。ER7B-C10机器人连杆的实际参数见表2。

图4 ER7B-C10机器人仿真模型

表2 ER7B-C10连杆参数（单位：mm）

3．2 正逆运动学仿真验证

调用Robotics Toolbox中的fkine函数，可以对上述建立的正运动学模型进行正确性验证［13］。将操作空间中末端点位姿所对应的关节变量值targ_ang带入模型中，若所得结果与fkine函数所得解相一致，则说明正运动学模型建立正确，重复多次验证可保证结果准确可靠。

调用Robotics Toolbox工具箱中ikine逆解函数指令来验证运动学逆解的方法存在一定的局限性，这是由于ikine函数运用的是迭代法来求解逆运动学，迭代的收敛性将可能引起无解或者漏解的情况［14］，不能完成上述运动学逆解验证的任务。因此，拟采用代入验证的方式来验证几何法计算运动学逆解是否正确，设计验算流程如图5所示。将预设位姿的值代入运动学逆解计算，得到的关节变量代回上述验算正确的正运动学模型中，只要得到的正运动学模型的解与预设位置的误差在合理的范围内，则说明上述几何法计算运动学逆解公式的推导正确。

图5 验证逆解流程设计

对运动学逆解需要充分考虑其存在性，即所取预设位姿的值必须在机械臂可达工作空间内才能够实现对运动学逆解的验证。4组在可达工作空间内的位置坐标见表3。

表3 预设位置坐标

将预设位置坐标代入上述几何法求解运动学逆解的公式中，所求得的各关节变量见表4。

表4 预设位置运动学逆解

在Matlab中使用验证正确的运动学正解模型来计算，由逆解计算出来的各个关节的关节变量带入正解模型，得到4组关节变量对应的位姿矩阵。

由位姿矩阵分析可得，所得位姿的第4列元素与给定位置Px、Py、Pz相比较，结果见表5。

从表5可知，预设位置与计算位置存在一定误差，引起误差的可能原因为：计算过程中保留小数点位数，导致数值近似处理，最终计算结果存在偏差，见表6。

表5 预设位置与计算位置比较结果

表6 坐标位置绝对误差

从表6可知，4组坐标绝对误差不大且在允许的范围内，即可认为：上述通过解析几何法求解ER7B-C10机器人运动学逆运动方程可行。

3．3 机器人动态仿真

轨迹规划的目的是生成运动控制系统的参考输入，以确保机器人完成轨迹的规划。规划是一组由期望轨迹的内插函数所得到的时间序列值构成的［15］。调用Robotics Toolbox工具箱中jtraj函数指令，对机器人关节空间进行从初始点到目的点过程中的五次插值多项式进行机器人运动轨迹规划，主要研究了机械臂末端位姿与六个关节变量之间的关系［16］。选取机械臂末端初始位置A的各关节变量init_ang＝［0 0 0 0 0 0］，目标点B的各关节变量tag_ang＝［－1.46088－0.27699 0.455 0.31 0 1.4451］，其中目标点B为机械臂在操作空间中的非奇异点，且机械臂运动到目标点B的过程中各关节变化较为直观，便于观测其运动的可行性。机械臂仿真模型3维动态仿真和末端运动轨迹如图6所示。

图6 模型轨迹仿真结果

机械臂6个旋转关节的位移变化曲线、速度变化曲线、加速度变化曲线如图7所示。从图7可知，机械臂末端从初始点A到目标点B的运动过程中运行轨迹连续且平稳，6个关节的位移变化曲线平滑且持续稳定，说明机械臂实现了由关节空间关节量变化到末端执行器在笛卡尔空间进行起始点到目标点之间运动的转化；速度、加速度的初值和末端值均为零，则说明机器人在两个点之间可以平滑地起停，进一步证明了ER7B-C10机器人在工作空间内运动的可行性。

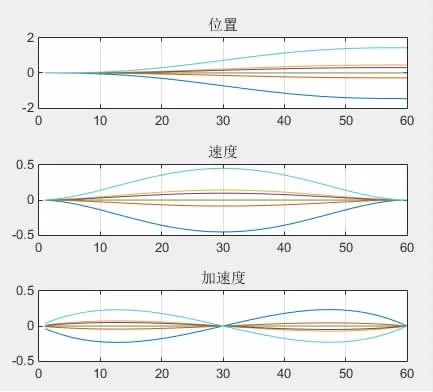
图7 关节位移、速度、加速度曲线

4 结束语

针对ER7B-C10机器人进行运动学分析，运用D-H法合理建立坐标系，推导出运动学正解，并针对解析法的计算量大、受奇异点影响大的缺点，选用另一种几何方法求解逆运动方程，利用Matlab进行机器人建模，设计运动学逆解验证方法。验证结果表明几何方法求逆可行，并在仿真中输出运动过程中各关节运动的位移、速度、加速度曲线。仿真结果表明了ER7B-C10机器人运动的可行性。本文研究为后续分析机器人动力学、轨迹规划提供了运动学参考。