附加黏滞和黏弹阻尼器的结构减震分析

田英侠，杨 萍

（西安工业大学建筑工程学院，西安710021）

引言

地震对建筑结构具有极强的破坏力，危害巨大，防震减灾工作仍旧是现今面临的一大难题，从传统的结构抗震研究到现在的隔震、减震研究都得到了专家们的关注。传统的抗震结构是通过增加建筑的结构刚度、承载力来改变其质量分布，从而达到“硬抗”地震的作用，这可保全结构不发生整体倾覆，却不能保证结构的经济安全。而黏滞阻尼器只为建筑结构提供阻尼，不提供刚度，不会导致结构自身周期缩短，而且其价格低廉、安装方便，国内代表性的消能减震应用实例有北京饭店、苏通大桥等［1］。

林绍明、周云［2］对附设阻尼器的结构进行分析，发现黏滞减震层布置在结构中部时，结构的顶层位移降低较为明显，布置在结构上部时，则底层剪力降低明显，研究在附设多个黏滞减震层时，采用计算公式对其位置和数量进行了优化布置。孟春光等人［3］以某不规则结构图书馆为例安装黏滞阻尼器，试验表明，黏滞阻尼器不仅在小震而且在罕遇地震作用时都有显著的减震效果，满足了大震不倒的抗震设防要求。沈绍东等人［4］以某RC框架结构为例，对设置屈曲约束支撑和附加黏滞阻尼器的减震效果进行了对比试验，结果表明在多遇地震下，黏滞阻尼器更能减少加速度的响应，而在罕遇地震下，黏滞阻尼器对结构内力的减少更为明显。周颖，张丹等人［5］做了关于在钢框架结构中设置黏滞阻尼墙的结构振动台试验，结果表明阻尼墙的附加阻尼对结构的位移提供了显著的控制能力，研究还发现有限元分析的结果和试验的结果是否吻合与响应对象和激励工况有关，Maxwell模型在阻尼墙中的运用有一定的局限性。兰香等人［6］推导了层间位移利用率与阻尼器布置位置和消能子结构梁柱刚度比两者间的关系，发现阻尼器居中布置时，层间位移利用率越大则附加阻尼越小。但该研究只考虑了阻尼器布置对层间位移的影响，没有选取对其他因素如层间剪力的影响来优化布置。季元景［7］提出以楼层剪力为减震目标，通过计算等效阻尼比来实现消能减震目标，研究指出设置黏滞阻尼器后可以均匀调谐各楼层的地震反应，避免有软弱层、薄弱层的出现。

韩建平［8］则对某一设有黏弹性阻尼器的16层RC框架结构和另一无控结构在多遇地震作用下的反应进行对比分析，发现前者的阻尼比得到显著提高，耗能能力增加，对地震的响应降低明显。李芮［9］通过分析得到了RC框架附加黏弹性阻尼器时，其钢支撑的动力响应、层间位移角、破坏过程及失效模式，研究具有非常重要的现实意义及广泛应用前景。陈敏［10］在论文中提出黏弹性阻尼器既为结构提供阻尼又提供刚度，因此黏弹性消能设计比黏滞阻尼器消能体系要复杂许多，研究从随机响应的方向出发，推导出黏弹性阻尼器在结构中的附加等效阻尼比的计算公式，使其消能减震特性可用阻尼比来表示，该方法能有效地简化附加黏弹性阻尼器的设计，与以往的方法相比，精确度更高也更安全。

周强、吕西林等［11］对三层单跨框架并联安装了金属阻尼器和黏滞阻尼器，并在此基础上进行了振动台试验，得出了两者的动力特性和减震效果。翁大根［12］针对附加金属消能器减震结构提出一种简化设计阻尼器的方法。王艮平等［13］为防止钢筋框架结构在地震作用下形成塑性铰，提出采用扇形黏弹性阻尼器，并通过低周反复加载试验，发现扇形黏弹性阻尼器能提高结构的水平承载能力，并能延缓塑性铰的出现。景铭等人［14］就提高黏滞阻尼器的性能、能量耗散能力，优化阻尼器位置布置，增大其受力抗变形能力等方面的问题进行了论述。M.Burgos［15］通过对某建筑进行非线性时程分析，以最大程度减小层间位移角、得到最高的附加阻尼比为目标进行了相关参数优化，发现将阻尼器安装在系统上部的减震效果优于安装在下部。I.Bras等［16］通过评估层间速度的功率谱来优化阻尼器在高层建筑中的位置。A.M.Puthanpurayil等［17］则提出了一种复合目标优化方法，该法同时考虑了初始成本与总体预期损失。乔峰等［18］人提出了基于实模态空间解耦极点配置算法来进行阻尼器优化设计，减少了阻尼器数量，降低了成本造价，达到了预期效果。消能减震器具有结构形式灵活、损伤部位可控、性能稳定等优点，将其设置到建筑结构中，可以直接提高其抗震能力。

综上所述，大多数研究仅用一种阻尼器，或者将黏滞阻尼器和金属阻尼器混合布置，而并没有对黏滞阻尼器和黏弹性阻尼器进行混合布置和相关参数优化。针对此，本文在建筑结构上结合附加黏滞阻尼器和黏弹阻尼器，研究不同安装位置的减震效果差异，寻求具有较好减震效果的布置位置。

1 阻尼器参数设置

本文将黏滞阻尼器和黏弹性阻尼器组合运用到建筑结构中，以减少其地震响应。一方面，黏滞阻尼器在给结构提供一定阻尼的同时不提供刚度，所以不改变结构的固有频率，此外还可以降低层加速度，但其价格昂贵，制作工艺繁琐且质量要求高，若整体建筑安装黏滞阻尼器会大幅增加造价。另一方面，黏弹性阻尼器虽然对层加速度降低不大，但安装简单方便，价格低且经久耐用，它不仅提供阻尼力，还因其本身有一定的刚度，能为结构提供抗侧移刚度从而减小结构周期。

1．1 黏滞阻尼器参数设置

黏滞阻尼器的筒内填充阻尼黏滞材料，筒内活塞上设置有少量小孔。在受到地震作用时，活塞开始移动，活塞与缸筒通过互相运动达到耗能的目的。黏滞阻尼器的耗能曲线图中，出力随指数α变化，这对耗能有较大的影响。黏滞阻尼器的耗能公式为：

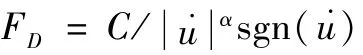
式中，C为黏滞阻尼器的阻尼系数，这里取3000 kN·S／mm2；˙u为阻尼器两端的相对运动速度；α为阻尼指数，这里取0.2。本文采用非线性流体黏滞阻尼器，使用斜撑布置。

1．2 黏弹性阻尼器参数设置

黏弹性阻尼器是由理想弹性元件和理想黏性元件串联或并联而得到的，其基本计算模型有：Kelvin模型，Maxwell模型，标准线性固体模型和Burgers模型。ETABS软件采用的是Maxwell模型，其总的应变为：

式中，γe为弹性元件的应变；γv为黏性元件的应变；γ为黏弹性阻尼材料的剪切应变。该模型的本构关系为：

式中，τ为黏弹性阻尼剪切应力；˙i、r为τ和γ的导数；p1和q1是由黏弹性材料确定的系数。在简谐应变激励下，由本构关系（2）可以导出：

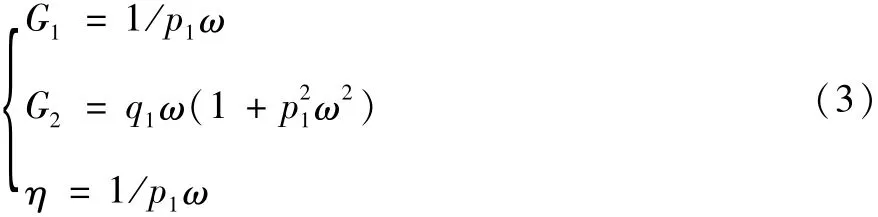
式中，G1为储存模量；G2为损耗模量；η为损耗因子。

黏弹性阻尼器的有效刚度Kd和有效阻尼Cd，通过下列公式求得：

式中，A和h分别为黏弹性层的剪切面积和厚度，这里A＝0.117 m2，h＝0.0025 m；ω为外部激励圆频率；储存模量G1＝2.068×103kN·m-2。由式（4）～式（5）可得：

G2＝2.294×103kN·m-2

Kd＝1.34×104kN·m-1

Cd＝0.59×104kN·m-1

将两种阻尼器混合的结构组合形式应用于框架结构的抗震中，使建筑在地震发生时减少结构振动，这不但可以克服单独设置黏滞阻尼器或黏弹性阻尼器的不足，而且有利于耗能减震设计，并能满足我国的相关规范原则，具有较好的理论和实际意义。而确定两种阻尼器最优的组合形式，具有较强的工程应用价值，能够促进减震技术在实际工程中的应用。

2 建筑结构模型

以9层钢筋混凝土（Reinforce Concrete Construction，RC）框架结构工程为例。该结构位于8度设防区，场地类型为II类，整体抗震等级为二级，抗震设计分组为第一组。柱混凝土为C45，梁和板为C40，梁柱纵筋均为HRB400，楼板厚为100 mm，其一层平面图如图1所示，三维实体结构图如图2所示。

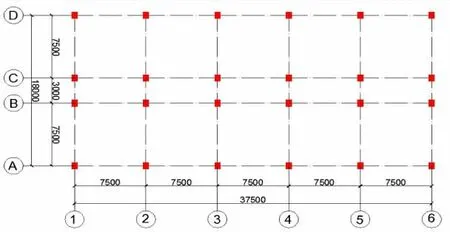
图1 9层RC框架结构工程的结构平面图（单位：mm）

图2 9层RC框架结构工程的三维结构模型图

使用PKPM软件对该建筑结构进行建模（无控结构），同时利用ETABS软件另建立了3种模型，分别为模型a（无控结构）、模型b（附加黏滞阻尼器）和模型c（附加黏弹性阻尼器），这4种模型的振型结果见表1。

将表1中四种模型的振型结果作对比分析。PKPM无控结构模型与ETABS模型a（无控结构）的最大振型差＝（0.919－0.843）／0.919×100%＝8%，说明使用ETABS软件进行分析可取得较精确的结果；ETABS模型b（附加黏滞阻尼器）与ETABS模型a（无控结构）的最大振型差＝（1.093－1.012）／1.093×100%＝7%，说明附加黏滞阻尼器后，结构的自振周期有一定缩短，但变化幅度不大；ETABS模型a（无控结构）与ETABS模型c（附加黏弹性阻尼器）的最大振型差＝（1.093－0.94）／1.093×100%＝13%，说明附加黏弹性阻尼器后，结构的自振周期缩短较明显。

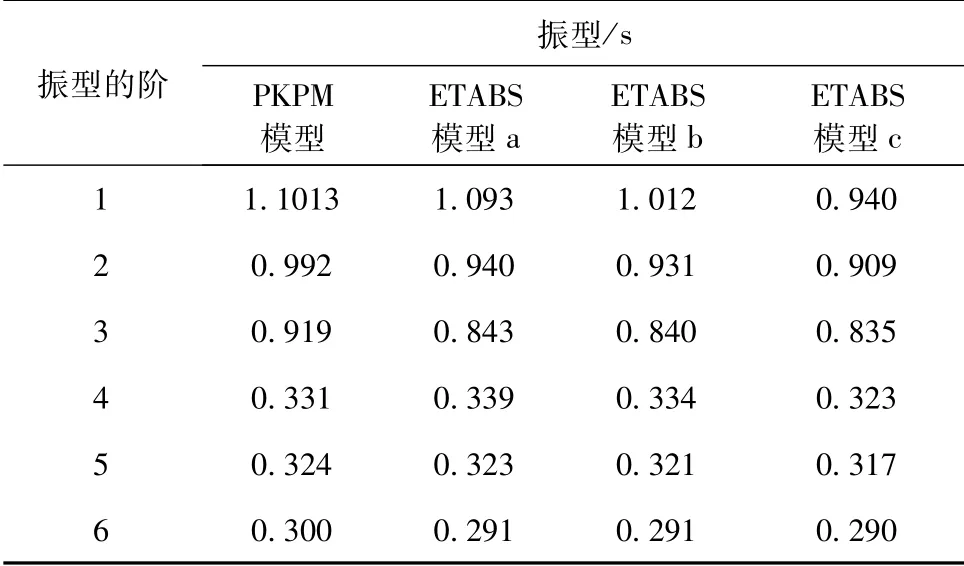
表1 PKPM模型与ETABS模型的振型结果

3 地震波选取

按照抗震规范的要求，从太平洋抗震研究中心（PEER）强震数据库中，选取适用于该结构类型的二类场地的五条地震动记录以及使用simqke软件生成的人工波，各地震波反应谱如图3所示，其中图3（a）为EI centro波截取前50 s加速度最大的时段，图3（b）为Taft波截取前30 s加速度最大的时段，图3（c）为人工波截取前40 s加速度最大的时段。人工波拟合曲线如图4所示。

从图3（a）～图3（c）可知，各地震波加速度最大值都在70 g左右。从图4可知，人工波反应谱与规范反应谱较吻合。

4 阻尼器布置

用有限元分析软件ETABS建立结构模型，按规则设置了黏滞阻尼器，通过设置非线性LINK单元来模拟消能器，此单元包括三个属性，分别为刚度K、阻尼系数C和阻尼指数α。此外，ETABS软件通过两个非线性连接单元来模拟黏弹性阻尼器，分别考虑阻尼和刚度两个性能，在X向或Y向布置单个黏弹性阻尼器，将附加阻尼（Cd＝0.59×104kN·m-1）和附加刚度（Kd＝1.34×104kN·m-1）这两者的非线性连接通过并联来模拟黏弹性阻尼器。通过以上方法建立了5种模型，各模型的阻尼器设置形式见表2。对这5类模型分别输入实强地震动和人工地震动，分析地震作用下结构模型的位移角变化。

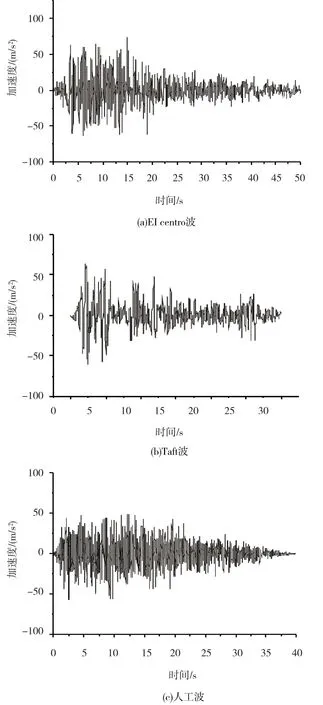
图3 各地震波反应谱

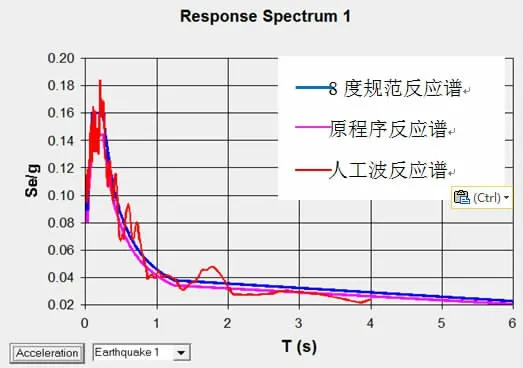
图4 地震波拟合曲线

表2 阻尼器布置类型

5 结果分析

分别向上述五种模型中输入各种类型地震波（人工波、EI centro波和TAFT波），得到各模型的层间最大位移角和层间最大位移，如图5～图7和图8所示。其中，图5～图7依次分别为人工波、EI centro波和TAFT波作用下的位移角，图8为最大层位移（以人工波为例）。

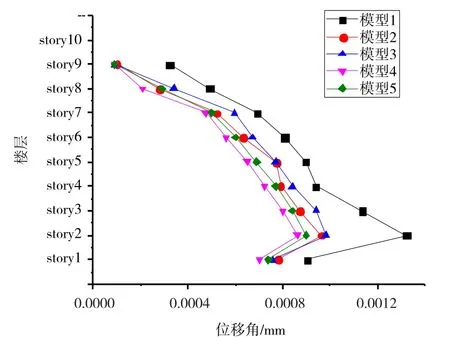
图5 人工波作用下的位移角

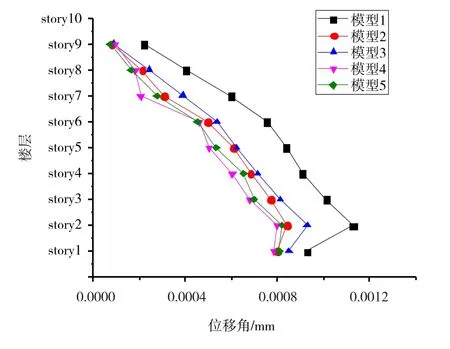
图6 EIcentro波作用下的位移角

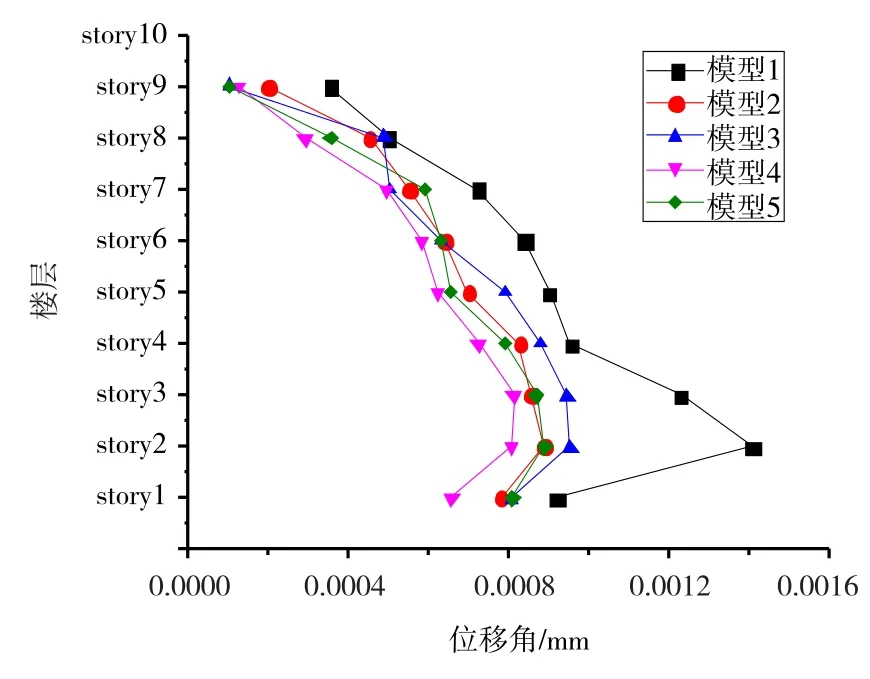
图7 TAFT波作用下的位移角

从图5可知，人工波作用下，各模型的最大位移角发生在二层；无控结构（模型1）的位移角为1.3×103mm，比其他模型的都大，但也能满足抗震规范的要求；结构单独设置黏滞阻尼器（模型2）的最大位移角为9.61×10－4mm，比无控结构的减少了27.2%；单独设黏弹性阻尼器（模型3）的最大位移角为9.8×10－4mm，比无控结构减少了25.7%；上层布置黏弹阻尼器结合下层布置黏滞阻尼器（模型4）的最大位移角为8.61×10－4mm，比无控结构的减少了34.7%；上层布置黏滞阻尼器结合下层布置黏弹阻尼器（模型5）的最大位移角为9×10－4mm，比无控结构的减少了31.8%。由此说明：当结构单独附加黏滞阻尼器或时黏弹阻尼器时，都能不同程度的提高结构模型的减震效果；而当两者组合起来附加到结构上时，减震效果更好；其中上层布置黏弹阻尼器结合下层布置黏滞阻尼器（模型4）的减震效果最好，位移角比无控结构的减少幅度最大。

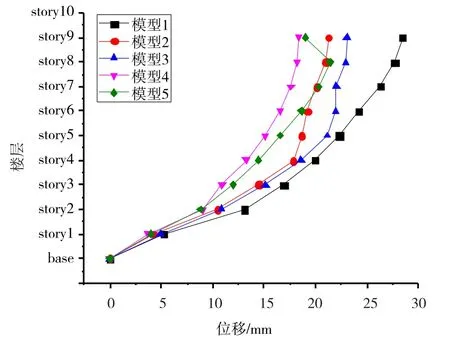
图8 人工波作用下的最大层位移

从图6和图7可知，在EI centro波和Taft波作用下，阻尼器布置位置对位移角的影响与人工波的影响在总体上相似，因此不再赘述。

从图8可知，人工波作用下，各模型都在第9层出现层间最大位移；无控结构（模型1）的最大位移为28.452 mm，是各模型中最大的；在结构中单独布置黏滞阻尼器（模型2）时，最大位移为21.240 mm，比无控结构的减少了25.3%；单独布置黏弹性阻尼器（模型3）时，最大位移为23.036 mm，比无控结构的减少了19.0%；上部布置黏弹性阻尼器结合下部布置黏滞阻尼器（模型4）时，最大位移为18.38 mm，比无控结构的减少了35.4%，减少幅度最大；上部布置黏滞阻尼器结合下部布置黏弹性阻尼器（模型5）时，最大位移为19.001 mm，比无控结构的减少了33.2%。由此说明：当结构单独附加黏滞阻尼器或黏弹阻尼器时，都能使其在遭遇地震时不同程度地减少最大位移；而当两者组合起来附加到结构上时，最大位移更小；其中，上层布置黏弹阻尼器结合下层布置黏滞阻尼器（模型4）时，最大位移最小，减震效果最好。

6 结束语

通过对附加阻尼器的RC框架结构的抗震性能进行分析，发现在结构中单独附加黏滞阻尼器的减震效果比单独附加黏弹性阻尼器的好；4种阻尼器布置模型（模型2～模型4）的建筑结构最大位移角和层间位移相对无控结构（模型1）的都有一定程度的减少，其中上层布置黏弹阻尼器结合下层布置黏滞阻尼器（模型4）的结构最大位移角和层间位移的减少幅值最大，说明模型4的阻尼器减震效果最明显。