资本性支出及折旧摊销预测模型——到期更新模型

■ 沈越火

资本性支出是指通过它所取得的财产或劳务的效益，可以给予多个会计期间所发生的那些支出。企业要维持目前的经营规模和经营活动的长期进行，到期的固定资产、无形资产等长期资产，应当进行更新。在企业价值收益法评估过程中，资本性支出常指机器设备、房屋建筑物、机动车辆、无形资产等长期性资本。资本性支出及折旧摊销，是企业价值收益法评估现金流量预测中的重要参数，固定资产权重比较大的企业价值的评估。

目前，对于资本性支出的预测，各评估机构的做法也不尽相同。有根据对历史资本性支出的分析，预测未来支出数；也有采用在可明确预测期，不考虑资本性支出，而在永续期，假设资本性支出等于折旧摊销数的方法；还有在基准日以后，假设资本性支出等于折旧摊销数；而对于折旧摊销的预测，各机构的做法基本一致，即根据被评估企业的折旧摊销政策，按基准日账面折旧摊销数预测。

我们知道，资本的折旧摊销年限，一般比资本的经济使用年限短。如果按基准日资本原值预测折旧摊销，会把折旧摊销年限到期日至资本更新日这段期间，本应不计提折旧摊销的资本，也进行了折旧摊销的计提，由于折旧摊销的抵税作用，虚增了企业的现金流量。

本文提出资本到期更新的资本性支出及折旧摊销预测模型，也就是资本的经济寿命年限一到期，马上进行更新；折旧摊销一到期，即刻停止计提折旧和摊销，并按新的资本性支出计提折旧和摊销。具体又分为两段式或年金式两个预测 模型。

企业价值收益法评估的收益预测期，评估机构采用的大多为两段式，第一段为可明确预测期，也就是基准日后的若干年作为一个期限，可明确预测期结束后作为另外一个期限，也就是通常说的永续期。为了便于理解，资本性支出及折旧摊销预测，相应也分为两段式，在可明确预测期和永续期分别制定不同的资本性支出和折旧摊销预测模型；所谓的年金式预测模型，也就是在基准日后，每年的资本性支出相等、每年的折旧摊销均相等的模型。

本文使用的字母所代表含义：C0—资本初始入账时原值；x1—资本购买时至评估基准日的时间；x2-可明确预测期时间长度；N-资本的经济寿命年限；n-资本的折旧摊销年限；g-资本物价增长平均指数；α-资本的年折旧摊销率（年折旧摊销金额与原值的比率）；DA-年折旧摊销金额；r-折现率。

一、两段式预测模型

（一）资本性支出预测两段式模型

在可明确预测期资本性支出的预测与估计，按照该项长期资本已经使用年限与剩余经济寿命来判断是否更新。如果N-x1≤0，即可更新，资本性支出=C0(1+g)N，否则，不需进行资本更新。下面重点介绍在永续期资本性支出预测模型。

1.如果第一次资本更新在可明确预测期之后，即x1+x2≤N。更新时间距离可明确预测期末的时间为t，资本性支出在可明确预测期末的现值为C。收益预测年限为无限期的情况下（下同），长期资本应该到期不断更新，以维持企业的永续经营。长期资本的更新第k次、更新价值Ck、更新距离可明确预测期末的时间t、在可明确预期期末的现值C，计算结果及情况如下表1：

表1

长期资本依次更新在可明确预测期末的现值，组成了等比数列，公比q=C2/C1=C3/C2=…Ck/Ck-1

=C0(1+g)2N(1+r)-(2N-x1-x2)/C0(1+g)N/(1+r)-（N-x1-x2）

=C0(1+g)3N(1+r)-(3N-x1-x2)/C0(1+g)2N/ (1+r)-(2N-x1-x2)

=…

=C0（1+g）kN（1+r）-(kN-x1-x2)/C0（1+g）（k-1）N/（1+r）-[(k-1)N-x1-x2]

通常，长期资产的长期平均物价增长率g会低于折现率r，所以，等比系数小于1（下同）。从而，某项长期资本到期不断更新时，在可明确预测期末的现值C1、C2、C3、…、CK-1、…组成了无穷递缩等比数列。其资本性支出在可明确预测期末的总现值S，可根据无穷递缩等比数列的求和公式求取：

将其变成年金，某项长期资本在永续期每一年的资本性支出C：

2.如果第一次资本更新在可明确预测期之前，即x1+x2＞N时，即资本的第一次更新在可明确预测期。永续期资本的更新第次k、更新价值Ck、更新距离可明确预测期末的时间t、在可明确预期期末的现值C，计算结果和情况如下表2：

表2

同样，资本在可明确预测期末的现值C2、C3、…、CK-1、…组成了无穷递缩等比数列。其资本性支出在可明确预测期末的总现值S，可根据无穷递缩等比数列的求和公式求取：

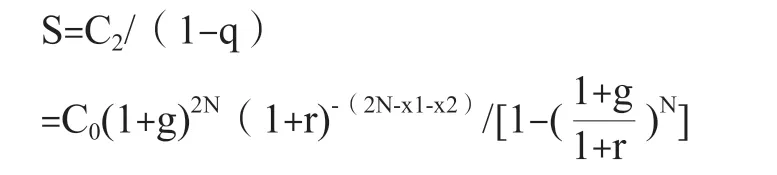
将其变成年金，某项长期资本在永续期资本性支出每年金额C：

（二）折旧摊销预测两段式模型

1.可明确预测期折旧摊销的预测

在可明确预测期的折旧摊销预测，结合相应的资本性支出预测进行。如果上一期资本没有更新，则本期的折旧摊销按原来的折旧摊销金额确定；如果上一期进行了资本更新，则按更新后的资本估计折旧摊销。在可明确预测期，运用逻辑函数进行运算就可以了。

2.永续期折旧摊销的预测

永续期折旧摊销的预测，分以下三种不同情况。

（1）如果第一次资本性支出在折旧摊销年限和经济寿命年限之间，即n＜x1+x2＜N时

1）第一次资本性支出金额C1=C0（1+g）N，年折旧摊销金额DA1=αC0（1+g）N，第一次资本性支出距离可明确预测期末的时间为N-x1-x2

第一次资本性支出所计提的折旧摊销在可明确预测期末的现值DA11=αC0（1+g）N/r×[1-（1+r）-n]×（1+r）-（N-x1-x2）

2）第二次资本性支出金额C2=C0（1+g）2N，年折旧摊销金额DA2=αC0（1+g）2N，第二次资本性支出距离可明确预测期末的时间为2N-x1-x2。

第二次资本性支出所计提的折旧摊销在可明确预测期末的现值DA22=αC0（1+g）2N/r×[1-（1+r）-n]×（1+r）-（2N-x1-x2）

3）第三次资本性支出金额C3=C0（1+g）3N，年折旧摊销金额DA3=αC0（1+g）3N，第三次资本性支出距离可明确预测期末的时间为3N-x1-x2。

第三次资本性支出所计提的折旧摊销在可明确预测期末的现值DA33=αC0（1+g）3N/r×[1-（1+r）-n]×（1+r）-（3N-x1-x2）

依次类推，第k次资本性支出所计提的折旧摊销在可明确预测末的现值DAkk=αC0（1+g）kN/r×[1-（1+r）-n]×（1+r）-（kN-x1-x2）

各次资本性支出所计提的折旧摊销在可明确预测期末的现值，也组成了公比q为首项为αC0（1+g）N/r×[1-（1+r）-n]×（1+r）-（N-x1-x2）的无穷递缩等比数列。根据无穷递缩等比数列求和公式，得出在永续期，各次资本性支出所计提的折旧摊销在可明确预测期末的现值之和S为：

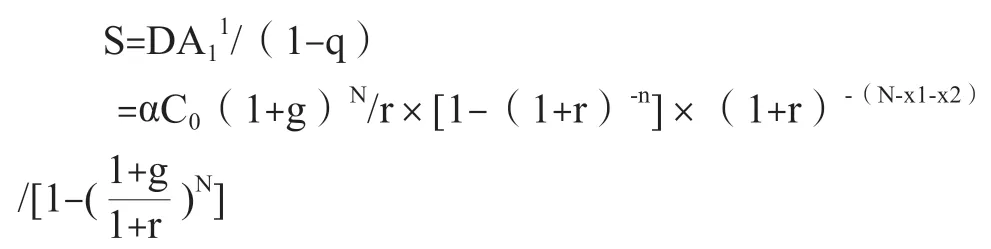
从而，在永续期，折旧摊销的年金DA：

（2）如果资本在可明确预测期末折旧摊销尚未计提完毕，在永续期还继续计提折旧或者摊销，即x1+x2＜n时，折旧摊销完毕至可明确预测期末的时间为（n-x1-x2），资本原值C0在永续期的折旧摊销在可明确预测期末的现值：

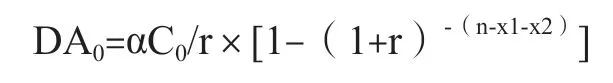
1）第一次资本性支出金额C1=C0×（1+g）N，其更新距离可明确预测期末的时间为N-x1-x2，年折旧摊销额DA1=αC0×（1+g）N。

第一次资本性支出所计提的折旧摊销在可明确预测末的现值DA11=αC0（1+g）N/r×[1-（1+r）-n]×（1+r）-（N-x1-x2）

2）第二次资本性支出金额C2=C0×（1+g）2N，其更新距离可明确预测期末的时间为2N-x1-x2，年折旧摊销额DA2=αC0×（1+g）2N。

第二次资本性支出所计提的折旧摊销在可明确预测末的现值DA22=αC0（1+g）2N/r×[1-（1+r）-n]×（1+r）-（2N-x1-x2）

3）第三次资本性支出金额C3=C0×（1+g）3N，其更新距离可明确预测期末的时间为3N-x1-x2，年折旧摊销金额DA3=αC0×（1+g）3N。

第三次资本性支出所计提的折旧摊销在可明确预测末的现值DA33=αC0（1+g）3N/r×[1-（1+r）-n]×（1+r）-（3N-x1-x2）

依次类推，第k次资本性支出金额Ck=C0×（1+g）kN，其更新距离可明确预测期末的时间为kNx1-x2，年折旧摊销额DAk=α×Ck=C0×（1+g）kN

第k次资本性支出所计提的折旧摊销在可明确预测末的现值DAkk=αC0（1+g）kN/r×[1-（1+r）-n]×（1+r）-（kN-x1-x2）

同样，可明确预测期之后，每次资本性支出所计提的折旧摊销在可明确预测期末的现值，也组成了公比q为首项为DA11的无穷递缩等比数列。所有资本性支出所计提的折旧摊销在可明确预测期末的现值之和S为：

从而，资本性支出所计提的折旧摊销，在永续期的每年金额DA：

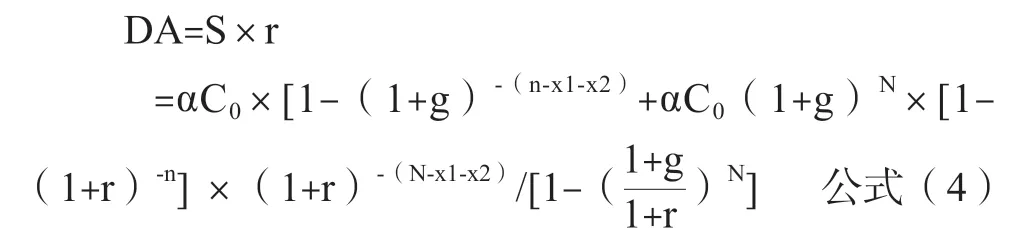
（3）当资本的第一次更新在基准日和可明确预期期之间，即x1+x2N时，资本的第一次更新距离可明确预测期末的距离为x1+x2-N。

1）第一次资本更新价值C1=C0（1+g）N，第一次更新的资本折旧摊销结束距离可明确预测期末的时间为n-（x1+x2-N）=N+n-x1-x2，资本年折旧摊销金额DA1=αC0（1+g）N

资本第一次更新在永续期折旧摊销价值在可明确预测期末的现值DA11=αC0（1+g）N/r×[1-（1+r）-（N+n-x1-x2）]

2）第二次资本更新价值C2=C0（1+g）2N，第二次资本更新距离可明确预测期末的时间为N-（x1+x2-N）=2N-x1-x2，年折旧摊销金额DA2=αC0（1+g）2N

资本第二次更新在永续期折旧摊销价值在可明确预测期末的现值DA22=αC0（1+g）2N/r×[1-（1+r）-n]×（1+r）-（2N-x1-x2）

同理，资本第三次更新在永续期折旧摊销价值在可明确预测期末的现值DA33=αC0（1+g）3N/r×[1-（1+r）-n]×（1+r）-（3N-x1-x2），第k次资本更新在永续期折旧摊销价值在可明确预测期末的现值DAkk=αC0（1+g）kN/r×[1-（1+r）-n]×（1+r）-（kN-x1-x2）。

从第二次资本更新开始，所有资本更新所计提的折旧摊销在可明确预测期末的现值，组成了公比q为首项为αC0（1+g）2N/r×[1-（1+r）-n]×（1+r）-（2N-x1-x2）的无穷递缩等比数列。利用无穷递缩等比数列的求和公式，求取从第二次资本性支出开始的所有折旧摊销在可明确预测期之和，加上第一次资本更新所计提折旧摊销的在永续期末的现值DA11，可得出资本在永续期所有的折旧摊销在可明确预测期末的现值之和S。

折旧摊销在永续期的年金DA=S×r

二、年金式预测模型

（一）资本性支出预测年金模型

假设某项长期资本第一次更新距离评估基准日的时间为N-x1，第一次更新价值C1=C0（1+g）N，第一次更新在评估基准日的现值C11=C0（1+g）N×（1+r）-（N-x1）；第二次更新距离基准日的时间为2N-x1，第二次更新价值C2=C0（1+g）2N，第二次更新在评估基准日的现值C22=C0（1+g）2N×（1+r）-（2N-x1）

依次类推，第K次资本更新在评估基准日的现值Ckk=C0（1+g）kN×（1+r）-（kN-x1）

评估基准日后资本更新在评估基准日的现值，依次组成了公比q为首项为C0（1+g）N×（1+r）-（N-x1）的无穷递缩等比数列。利用无穷递缩等比数列的求和公式，得出基准日后资本性支出在评估基准日的总现值S。

从而，采用年金法预测的基准日后资本性支出每年的金额C：

（二）折旧摊销预测年金模型

用年金法预测资本的折旧摊销，分以下两种 情况。

1.评估基准日折旧摊销已经完毕，即x1n，资本的第一次更新价值C1=C0（1+g）N，资本第一次更新距离评估基准日的时间为N-x1，资本第一次更新后年折旧摊销金额DA1=C0（1+g）N

第一次资本更新所计提的折旧摊销金额在评估基准日的现值DA11=C0（1+g）N/r×[1-（1+r）-n]×（1+r）-（N-x1）

资本的第二次更新价值C2=C0（1+g）2N，第二次更新距离评估基准日的时间为2N-x1，第二次更新所计提的年折旧摊销金额DA2=×C0（1+g）2N

第二次资本更新所计提的折旧摊销金额在评估基准日的现值DA22=αC0（1+g）2N/r×[1-（1+r）-n]×（1+r）-（2N-x1）

依次类推，第k次资本更新所计提的折旧摊销金额在评估基准日的现值DAkk=αC0（1+g）kN/r×[1-（1+r）-n]（1+r）-（kN-x1）

资本更新所计提的折旧摊销金额在评估基准日的现值，也组成了公比q为首项为C0（1+g）N/r×[1-（1+r）-n]×（1+r）-（N-x1）的无穷递缩等比数列。利用无穷递缩等比数列的求和公式，得出基准日后所有折旧摊销现值在评估基准日的总和S。

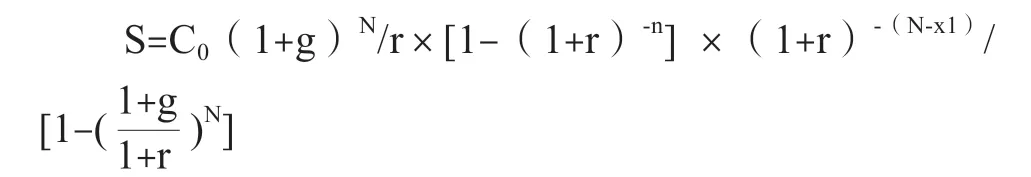
从而，评估基准日后所有折旧摊销预测的每年金额DA：

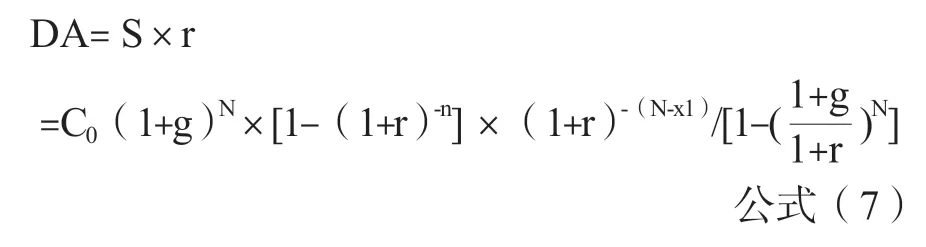
2.资本在评估基准日折旧摊销尚未完毕，即n＞x1，折旧摊销完毕距离评估基准日的时间为n-x1，按原始入账原值C0计算的年折旧摊销金额DA0=C0，按原始资本原值折旧摊销金额在评估基准日的现值DA00=C0/r×[1-（1+r）-（n-x1）]

第一次资本更新价值C1=C0（1+g）N，第一次资本更新距离评估基准日的时间为N-x1，第一次资本更新的年折旧摊销金额DA1=C0（1+g）N，第一次资本更新所计提的折旧摊销金额在评估基准日的现值DA11=C0（1+g）N/r×[1-（1+r）-n]（1+r）-（N-x1）

第二次资本更新价值C1=C0（1+g）2N，第二次资本更新距离评估基准日的时间为2N-x1，第二次资本更新的年折旧摊销金额DA2=C0（1+g）2N，第二次资本更新所计提的折旧摊销金额在评估基准日的现值DA22=C0（1+g）2N/r×[1-（1+r）-n]（1+r）-（2N-x1）

依次类推，第k次资本更新所计提的折旧摊销金额在评估基准日的现值DAkk=C0（1+g）kN/r×[1-（1+r）-n]（1+r）-（kN-x1）

各次资本更新所计提的折旧摊销在评估基准日的现值，也组成了公比q为首项为C0（1+g）N/r×[1-（1+r）-n]（1+r）-（N-x1）的无穷递缩等比数列。利用无穷递缩等比数列的求和公式，得出基准日后折旧摊销现值在评估基准日的总和S。

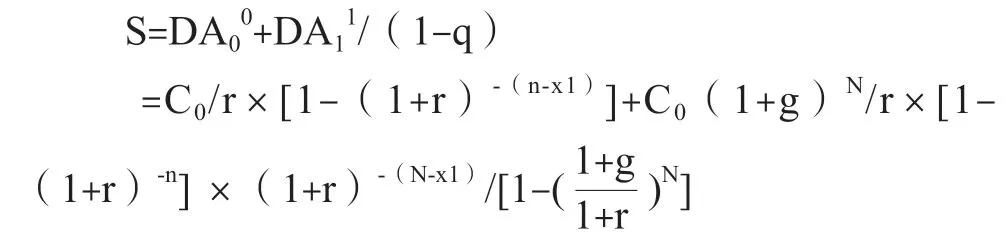
从而，预测的折旧摊销在评估基准日后的每年金额DA：

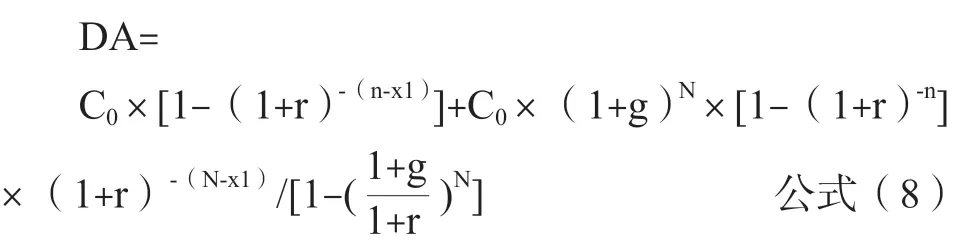
利用逻辑函数，把这些公式录入需要预测的资本所在的execl评估明细表，可以很方便地进行资本性支出和折旧摊销预测。