基于未确知测度理论与市场法的绿色翡翠手镯定价模型
■ 徐璐琳 李忠武
根据中国社科院发布的2017年《社会蓝皮书》,2016年1月至9月,全国居民人均可支配收入累计17 735元,同比名义增长8.4%。中国社会的总体收入差距2009年以来不断缩小,全国居民收入分配基尼系数从2008年的0.491下降到2015年的0.462。收入分配差距缩小,从社会阶层结构来说,意味着中等收入群体规模的扩大,因此也预示着人们对珠宝首饰的需求长期内应存在可持续增长。另一方面,据中宝协统计数据,2016年我国珠宝业终端市场销售额仍保持在5 000亿人民币以上,依然是世界主要珠宝市场之一。其中,翡翠玉石凭借其独特的艺术价值、文化价值及投资价值等尤其受国人偏爱。同时,作为资本密集型产业,珠宝业对资本有着巨大需求。随着其行业成长性逐渐受到社会认可,我国珠宝企业的融资需求和融资能力也在不断提升,而不论是抵押贷款还是更加前沿的资产证券化等渠道都要以其准确、可靠的价值评估为基础。因此,客观、公正、准确地进行翡翠价格评估有着其深远的现实意义。
一、国内外研究现状
(一)奢侈品定价研究现状
张鹏飞等(2013)通过珠宝与奢侈品在五个维度方面的比较,发现珠宝产品在稀缺性,给消费者带来的审美感受及耐久性等层面与奢侈品比较接近,而翡翠在我国需求较大,稀缺的高质量翡翠价格较高,是奢侈品类型的珠宝产品。[1]Yookyung Hwang等(2014)探讨了低、中、高价格对消费者奢侈品牌选择的影响,发现在购买名贵稀有奢侈品时,需求和价格呈现倒U型关系。[2]Erdös,P等(2010)采用基于非参数方法的方差比检验来检测美国艺术品拍卖价格的随机游走分量的大小,发现美国艺术市场的随机游走假说和弱有效性至少在过去的64年里是不能被拒绝的。[3]N.Anido Freire从工艺生产,原材料,工匠的知识、技能和艺术天赋的角度分析奢侈品价值。[4]Harris(2017)提出了一个黄金价格指数,该指数是以不同货币计价的黄金价格的几何加权平均值,其权重与全球黄金市场上每个国家的市场实力成正比,使市场参与者能够将全球汇率变化中黄金“内在”价值的变化分开。[5]
(二)翡翠定价影响因素及其量化探索研究现状
李济(2010)对翡翠的矿物组成、化学成分、结晶习性、结构、力学性质及翡翠的常规鉴定方法和红外光谱在翡翠鉴定中的应用进行了论述,提出了对翡翠的颜色、透明度、质地、净度、质量大小等进行品质分级并对其对价值评估的影响进行了阐述。[2]《翡翠分级》国家标准根据翡翠的颜色将翡翠分为翡翠(无色)、翡翠(绿色)、翡翠(紫色)、翡翠(红-黄色)几个类别,并从颜色、透明度、质地、净度四个方面对翡翠进行级别划分,并从材料应用设计和加工工艺两方面对翡翠的工艺价值进行评价。[7]
孙静昱等(2009)针对翡翠价格与其质量因素之间的复杂、不确定关系的特性,提出利用特尔斐法来判定各权重之间关系[8]张黎力等(2017)运用色度学HSL颜色空间模型通过一系列针对绿色翡翠颜色数据的分析归类,最终得到其各自HSL数值范围及阈值,然后再运用肉眼感官和Gemdialogue色卡进行分级验证。[9]许如彭等(2007)以翡翠作为混浊媒质建立数学模型,采用混浊媒质的库贝尔卡-芒克近似理论定理分析和计算其漫反射系数(S)、吸收系数(K)及材料无限厚度的光谱反射系数(R∞)量值来表征翡翠的颜色和透明度,从而进行翡翠品质的定量分析。[10]杨迪威(2010)构造了一个多影响因子的翡翠评价3层BP网络模型,对翡翠戒面样本进行了综合估价。[11]
二、基于未确知测度模型的翡翠手镯定价模型
未确知测度模型是基于随机统计和混沌理论的一种不确定性理论,该模型充分吸收行业专家的技术经验和主观测评,而对于被评价者的客观性指标,则能够不断获取其属性状态及其未确定程度,展开属性的未确知性测度,并根据各属性的重要性水平,设定属性的权重值,最终达成主观性指标与客观性指标的统一。[12]本文将利用未确知测度理论构建翡翠分级评价体系。
(一)确定翡翠手镯评价指标
基于《GB/T23885-2009 翡翠分级》的分级规则,选取颜色、透明度、质地、净度及工艺五个指标,对每个样品的五个指标参照国标以100分为满分进行评分。
(二)利用熵权法计算指标权重
根据熵的特性,我们可以用熵值来判断某个指标的离散程度,指标的离散程度越大,该指标对综合评价的影响越大。而在翡翠手镯的评估中,某一评价指标评分离散程度越大,则其越能够显示翡翠的异质性、区分翡翠等级,因此可根据各项指标的变异程度,利用信息熵这个工具,计算出翡翠手镯各评价指标的权重,为其多指标综合评价及后续定价提供依据。
1.原始数据的收集与整理
翡翠饰品种类繁多,如戒面、手镯、吊坠等,且对于不同品类的翡翠饰品,颜色、透明度等各项指标在价格评估时的权重不尽相同。因此,为了保证翡翠各评价指标权重的一致性以及运用市场法估价时,所选参照对象更具可比性,本文选择翡翠手镯这一特定品类的数据进行研究。从武汉某珠宝商城选取108件具有代表性及广泛性的样品,利用样品1至样品100建立翡翠手镯估价模型,并用该模型对样品101至样品108进行估价。
模型中,xi表示第i件样品,i=1,2,…,108;xi的5个指标变量分别为颜色(i1),透明度(i2),质地(i3),净度(i4)及工艺(i5),对每个样品的五个指标参照国标以100分为满分进行评分,如x11=88.1表示样品1的颜色得分为88.1。则形成的原始数据矩阵为:

2.数据标准化处理
由于各指标的量纲、数量及均有差异,所以为消除因量纲不同对评价结果的影响,需要对各指标进行标准化处理:
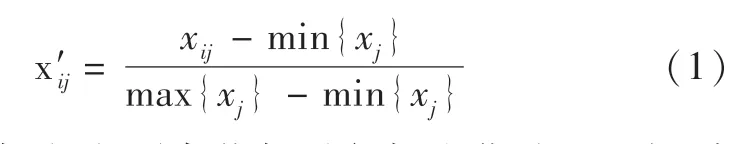
运用公式(1)对各指标进行标准化处理,得到矩阵:

3.计算第j项指标下第i个样品占该指标的比重
计算公式为:

运用公式(2)计算第j项指标下第i个样品占该指标的比重得到比重矩阵Y={yij}108×5

4.计算指标信息熵值e和信息效用值d
计算第j项指标的信息熵公式为:
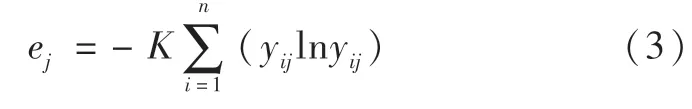

5.计算评价指标权重
第j项指标的权重为:

(二)运用聚类分析为待评估对象选择参照样品
聚类分析是将样品按照品质特性相似程度逐渐聚合在一起,相似度最大的优先聚合在一起,最终按照类别的综合性质多个品种聚合,从而完成聚类分析的过程。[13]市场法正是通过选择相同或相近的,近期已成交资产(作为参照物资产)的市场交易价格为基础,并对类似样品的其成交价格作适当修正进行估价。而利用聚类分析可以将相似样品聚合在一起,从而为寻找市场法所需的参照样品提供依据。
本文根据颜色、透明度、质地、净度、工艺的相似程度对108件翡翠手镯样品采用离差平方和法(Ward 法)进行个案(Q 型)系统聚类分析。聚类分析谱系图(图1)可知,在类间距离=2.5时,108个品种样品分为 7类,聚类结果如表1所示。
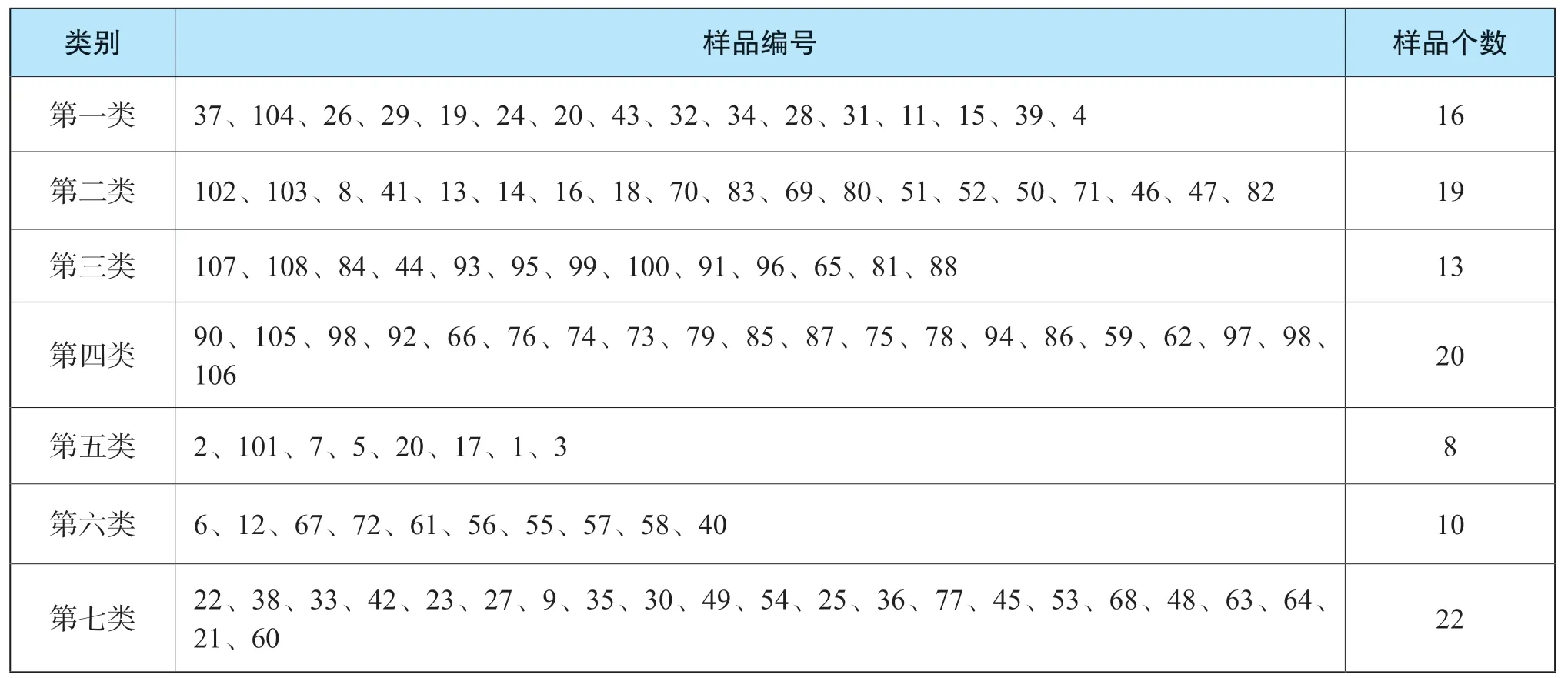
表1 样品系统聚类结果

图1 聚类分析谱系图
遵循市场法的基本原理,考虑待估样品实际情况,并结合聚类分析结果,为待估样品101至样品108分别选择同一类别最接近的三个参照样品,运用本文模型计算待估翡翠手镯价格,然后分析模型评估结果与手镯实际售价间的差异。待估样品和对应参照样品编号如表2所示。

表2 待估样品及对应参照样品编号
(三)运用层次分析法(AHP)计算市场法定价过程中各参照样品的权重
层次分析法是萨泰教授(A.L.Saaty)提出的一种综合定性与定量分析,模拟人的决策思维过程,以解决多因素复杂系统,特别是难以定量描述的社会系统的分析方法。在用市场法评估翡翠手镯价格时,因为各参照样品与评估对象的可比程度不同,因此若对参照样品的调整价格采取简单的算术平均作为最终估价难免造成误差,而AHP可以将各样品权重决策作为一个系统,按照分解、比较判断和综合的思维方式进行决策,并且将定性与定量分析相结合,在充分利用专家鉴定技术的同时又防止过分主观的判断。
1.建立层次结构模型
受文章篇幅所限,这里仅以样品101为例,详述运用层次分析法(AHP)计算市场法定价过程中各参照样品的权重,继而得到其评估价格的过程,其余样品仅给出计算结果。评估对象及参照样品各指标得分及在熵权法确定的指标权重下的加权平均分如表3所示。
则构造出层次结构模型如图2所示。
2.构造判断矩阵
记A1到A3分别表示样品2,样品5,样品7,通过样品各指标得分及加权平均得分相近程度及专家建议构造判断矩阵,如表4。
3.层次单排序及一致性检验

表3 评估对象及参照样品各指标

图2 层次结构模型

表4 矩阵表
(四)运用市场法确定待估样品价格
目前,翡翠饰品定价主要采用市场法。在运用市场法进行翡翠价值评估时需要确定各修正系数及各参照样品价值的权重。如果仅用算术平均法难免不够精确,因此本文通过熵权法确定翡翠饰品各分级指标权重,运用聚类分析选择参照样品并通过层次分析法确定各参照样品的权重,使翡翠饰品估价更加合理、客观、公正。
记各指标特征差额的权重分别为w1,w2,…,wn,则评估对象价值=参照物成交价格±基本特征差额1×w1×n±基本特征差额2×w2×n±…±基本特征差额n×wn×n。
通过熵权法计算出颜色、透明度、质地、净度和工艺五个指标的权重依次为:0.27,0.25,0.28,0.11和0.09,;通过层次分析法(AHP)计算出参照样品2、5、7的权重分别为0.59,0.32,0.09。
则,由样品2的价格通过修正后确定的估价为:


表5 待估样品模型估价与实际价格
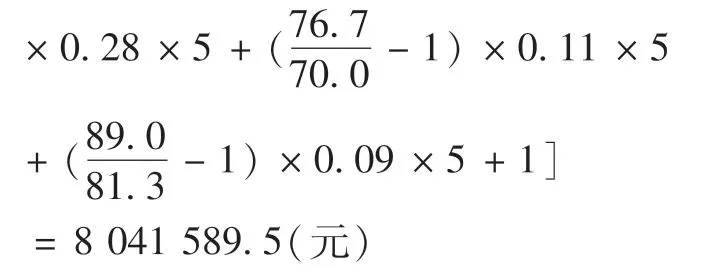
由样品5的价格通过修正后确定的估价为:

由样品7的价格通过修正后确定的估价为:

同理可得待估样品102至108的价格,同时计算出评估价格p与实际价格的差异百分比以分析模型评估价格与实际售价的差异:

三、结论与展望
本文以《翡翠分级》国家标准为依据,以中档绿色翡翠手镯为研究对象,选取颜色、透明度、质地、净度和工艺五项评估指标。以样品101至108作为待评估对象,并参照聚类分析结果选择各自参照对象,而后利用AHP的未确知测度模型确定各个参照样品的权重,最后得出待估样品的评估价格。从熵权法确定的各指标权重可以看出颜色、透明度及质地对翡翠手镯的价格影响较大。由于翡翠市场自身特点,其价格受到品牌溢价、价格协商等因素影响,浮动区间较大,从模型估价与实际价格的对比可以看出,部分翡翠饰品实际售价围绕其估价有较大浮动,但一般认为在同一数量级都是可以接受的,而大部分样品实际价格与模型评估价格接近,说明该定价模型不仅具有理论基础,与目前翡翠手镯市场定价实践也大致相符合。
为了对翡翠饰品价值评估的规范化、合理化、准确化进行探索,本文运用基于熵权-AHP的未确知测度模型,对市场比较法进行完善。并且,在翡翠分级、评估过程中,熵权法可以被进一步运用。例如,颜色指标又包含色调、彩度及明度三个二级指标,这些二级指标对其颜色评估的权重可以运用 熵权法进行确定;再如,工艺指标的确定可以采取以下方法:由多位专家对样品工艺进行打分,然后通过熵权法确定各专家评分的权重,继而计算出最终得分。

