基于动态摩擦因数磨损系数的先进高强钢模具寿命研究∗

聂 昕，王成龙

(湖南大学，汽车车身先进设计制造国家重点实验室，长沙 410082)

前言

为满足汽车轻量化和安全性能的要求，先进高强钢(AHSS)作为一类新材料，由于其比强度较大，被越来越多地应用于汽车白车身冲压件中。然而由于这类材料强度、硬度较大，在冲压成形时需要较大的成形力，同时出于对环境保护的考虑，须减少润滑介质的使用，导致成形过程中出现较大的成形摩擦力，因此先进高强钢使用量日益增加，会加剧模具的磨损，增大模具维修成本。模具磨损是影响模具寿命的主要因素，因此精确计算磨损成为预测模具寿命的必然途径。然而磨损是一个动态非线性过程，与工具几何形状、表面质量、材料性能、成形参数和润滑等因素有关。这些过程参数相互作用，使预测磨损成为一个很复杂的问题[1]。

对于磨损系数而言，目前常用的方法是通过实验测得一定条件下的磨损量而计算得到。P.P.Michael等[2]研究表明，整个冲压过程中接触压力是随着时间不断变化，且随着冲压过程的进行，板料成形的状态不断变化，因此会造成板料同一节点在不同时刻的应变速率不同[3]，即该节点相对于模具的速度不断变化。C.O.Paul等[4]通过实验测得不同速度下磨损率会发生变化，且在低速条件下变化比高速情况下更敏感。R.N.Rao等[5]利用销盘实验研究不同速度及压力条件下高强铝合金的磨损情况，发现压力和速度的变化对磨损系数的影响很大。F.E.Kennegy等[6]研究表明，不同速度下合金的磨损率变化很大，针对具体的冲压模具而言，因为冲压过程中磨损条件是不断变化的，所以只通过一组数据来预测磨损，精度不高。Wang C.S.等[1]根据磨损过程中磨损率的变化将磨损系数K分3阶段定义并通过销盘实验分别测得，提高预测精度。

传统的板料成形数值仿真过程多采用库伦摩擦模型，即将摩擦因数设定为一个恒定的值[7－8]，以此来简化计算。然而成形过程是动态变化的过程，在此过程中界面节点的正压力和相对滑动速度随着成形的过程不断变化，而正压力及滑动速度的变化会引起摩擦因数不断变化[9－10]。此外由于高强钢冲压过程中产生较大的界面压力，而当压力过大时使用库伦摩擦模型会因产生较大的剪切应力而失效[10]。

本文中针对冷冲压的动态变化过程，研究摩擦因数与磨损系数随正压力和相对滑动速度而变化的关系。提出摩擦因数和磨损系数随正压力与相对滑动速度动态变化的模型，同时结合模具表面镀层硬度动态变化的模型来计算磨损，进而预测模具寿命。

1 磨损模型与磨损计算方法

模具磨损失效有黏着磨损、磨粒磨损、氧化磨损和疲劳磨损等模式，而对于冷冲压模具的磨损失效主要由黏着磨损造成[11－12]。

1.1 黏着磨损

黏着磨损是在法向载荷作用下，两接触表面的半球状微凸起发生黏合，当两表面发生相对移动时，微凸起之间的合力大于材料分子之间的附着力，材料就会从一个表面转移到另一个表面而发生黏着磨损[13]。

黏着磨损常用的计算模型为Archard磨损模型，可简化为

式中：h为磨损深度；K为磨损系数；p为某节点正压力；v为相对滑动速度；H为被磨表面材料硬度。

1.2 镀层

对于先进高强钢冷冲压模具表面做镀层处理，而此时模具表面的综合硬度会受到镀层和基质材料硬度的影响，且随着磨损的进行镀层厚度减小，综合硬度也随之减小[13]。A.M.Korsunsky等[14]提出的较为合理的基于镀层系统综合硬度的计算方程为

式中：Hc为综合硬度；Hf为镀层表面硬度；Hs为基质硬度；k为厚度影响系数，由实验测得数据拟合得到；β为相对压痕深度，β＝t0/c，t0为实验中压痕深度，c为镀层厚度。

计算冲压成形过程中模具表面的综合硬度随磨损深度的变化，故此处压痕深度为磨损深度，可得

式中：α为镀层与基质表面维氏硬度之比；hi为第i次冲压节点的磨损深度。

1.3 动态摩擦因数和磨损系数

在冲压成形过程中模具受到的压力和板料相对滑动速度随冲压模具的运动而不断变化，而压力及相对滑动速度的变化会对模具与板料的摩擦因数和模具磨损系数产生影响。

以压力和相对滑动速度为变量进行摩擦磨损正交实验得到不同压力条件和速度下摩擦因数值，利用曲线拟合得到不同压力下摩擦因数随速度变化的关系式，即

利用拉格朗日插值法得到在速度v＝vτ条件下，摩擦因数随压力变化的函数为

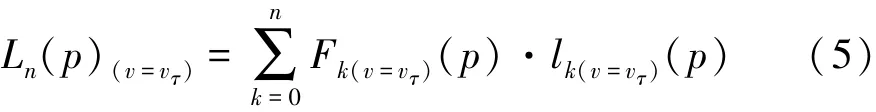
式中：lk为插值基函数，；n为正交实验中压力的变化个数，n＝1，2，3，…；p为正压力。

通过上述实验，测量并计算不同条件下的磨损系数和摩擦因数，并通过曲线拟合得到磨损系数随压力和相对滑动速度变化的关系式，即

式中：K为磨损系数；C1为常数；p为压力；v为相对滑动速度；x，y分别为拟合得到的压力和相对滑动速度的指数。

1.4 耦合磨损计算

将动态磨损系数模型、镀层硬度变化模型与Achard磨损计算模型进行耦合来计算磨损。将式(6)代入式(1)得到基于动态磨损系数的磨损深度计算模型：

将式(3)代入式(7)得

式中：r与t为表示位移与时间的参数；i表示第i次冲压；hi(r)表示模具型面上任意一点在第i次冲压过程中的磨损深度；pi(r，t)和vi(r，t)分别表示在第i次冲压过程中模具型面上任意一点在t时刻所受到的正压力及其相对于模具的滑动速度；ti表示第i次冲压过程的时间。则n次冲压累积磨损量为

1.5 计算流程

图1为基于动态摩擦磨损系数的模具寿命预测流程图。

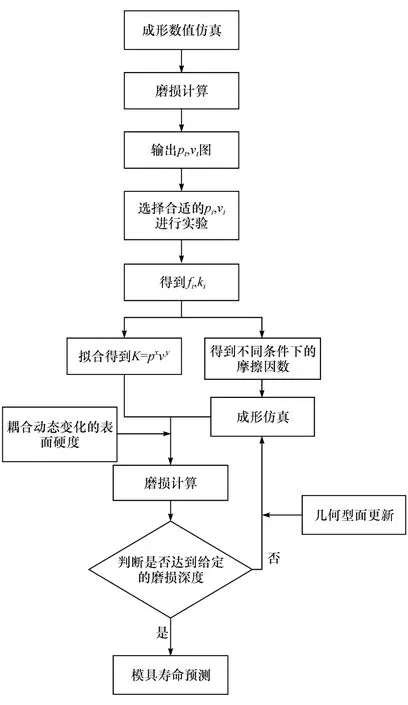
图1 模具寿命预测流程图

2 实验程序

为测得冲压成形过程中不同压力和速度条件下磨损系数和摩擦因数，须进行销盘摩擦磨损实验。

2.1 冲压仿真

以某车型左前纵梁加强板为例，进行冲压仿真。实际中为控制板料流动和节省时间进而提高生产节拍，模具在合模阶段为空行程，因此速度较快，为500 mm/s；而在拉延阶段，模具运动速度较慢，速度为200 mm/s。参照实际生产数据，分别设置模具合模和拉延速度。板料材料为先进高强钢DP780，板料厚度为1.0 mm。实际生产中，为降低模具磨损，提高板料流动性，会在模具表面喷洒润滑剂。对于先进高强钢的成形，由于其成形力较大，因此先进高强钢拉延模具的磨损常常发生于边界润滑状态中[15]，而边界润滑的摩擦因数在0.1～0.3之间，工程中对于高强钢冲压成形仿真中的摩擦因数经验值一般取0.15[10]。

图2和图3分别为利用LS-DYNA对该零件进行拉延成形仿真中某节点的压力和相对速度随时间步的变化关系。

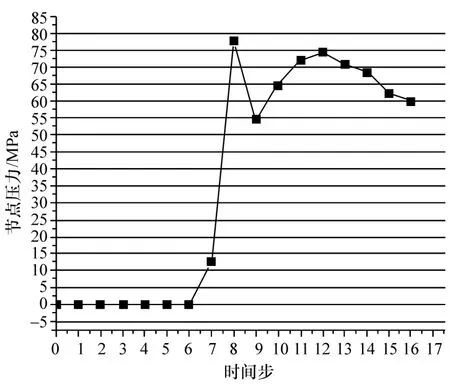
图2 节点压力随时间步的变化关系

图3 节点相对速度随时间步的变化关系

2.2 实验材料

以常用高强钢冲压模具材料Cr12MoV制作长度为15 mm、直径为5 mm、端头为1mm×45°倒角的销，要求硬度为58～62HRC。将销试样放入980～1 040℃的电阻炉中加热，使用油淬火。采用HVS-1000型显微硬度计和HR-150DT电动洛氏硬度计测量表面不同位置的硬度，至少测量3次，然后求出试样的平均硬度分别为305 HV和60.5 HRC。

实际生产中Cr12MoV材料模具虽然硬度很高，但用于高强钢冲压时仍有较大磨损，影响其使用寿命，因此工艺上需要对模具表面进行处理以提高其硬度和耐磨性能。渗硼设备为盐浴炉，盐浴成分包括供硼剂、还原剂和添加剂。当盐浴温度加热至约950℃时，将试样浸入盐浴中，保温6 h后取出，油淬，180℃回火2 h，即得实验所需的渗硼试样。对试样进行激光淬火，淬火方法参照文献[16]。淬火后使用HVS-1000型显微硬度计和HR-150DT电动洛氏硬度计测量试样表面不同位置的硬度，并求出平均值分别为1 303 HV和68 HRC。此外对淬火后的试样进行界面镀层厚度测量，得到镀层厚度约为52.8μm。

双相钢DP780作为一种比强度较高的先进高强钢，广泛应用于汽车车身加强件中。以DP780制作直径为40 mm、厚度为5 mm的销盘。图4为销盘磨损实验示意图，销磨损轨迹中心半径ro为15 mm。

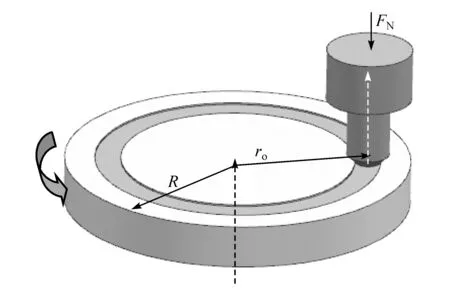
图4 销盘磨损实验示意图

两种材料的化学组成成分如表1所示。

2.3 实验步骤

根据图2和图3所示的某节点的压力及速度的变化关系取4组速度及其对应的压力作为变量进行摩擦磨损实验，所取速度分别为 47.12，94.25，141.37和 212.05 mm/s；所取压力分别为 4.95，24.76，42.44 和 70.74 MPa。

为实验方便，将线速度转化为角速度，对应的角速度分别为 π，2π，3π 和 4.5π s－1；利用式(10)和式(11)将压力转化为载荷，施加载荷分别取为140，700，1 200和2 000 N，实验中所设置的正交实验参数见表2。

表1 实验材料化学成分

式中：m与n分别代表实验变量载荷和速度的编号；F(m，n)为任意一组实验的载荷；p(m，n)为对应转化的压力(压强)；ω(m，n)为任意一组实验的角速度；v(m，n)为对应的线速度；A为实验中销与盘的接触面积，因材料磨损较小，故假设各组实验过程中销与盘的接触面积不变。

式中：ρ为材料密度，ρ＝7850 g/mm3；L(m，n)为各组实验磨损轨迹长度；t为磨损时间。

观察各组实验摩擦因数变化，待各组摩擦因数变化稳定后记录其平均值。

2.4 实验结果

实验结果见表3。

2.5 结果分析与曲线拟合

2.5.1 摩擦因数

基于表2中正交实验测得的各摩擦因数结果，得到不同压力条件下摩擦因数随相对速度的变化关

以上述4组速度和压力值为变化的实验条件进行摩擦磨损实验，其它实验条件保持不变，实验温度为室温(25℃)，相对湿度为 30%～33%。采用MMW-1A型多功能立式摩擦磨损试验机进行实验，每组数据进行3组实验，每组实验磨损1 h，实验前后每组的销在丙酮和乙醇中超声波处理，以去除表面附着物防止影响实验结果。

实验前后，使用最小刻度为0.1 mg的电子分析天平测量每组销磨损前后的质量变化量ΔM。假设忽略磨损材料密度的不同，由式(12)和式(13)求出每组实验黏着磨损系数为系，如图5所示。

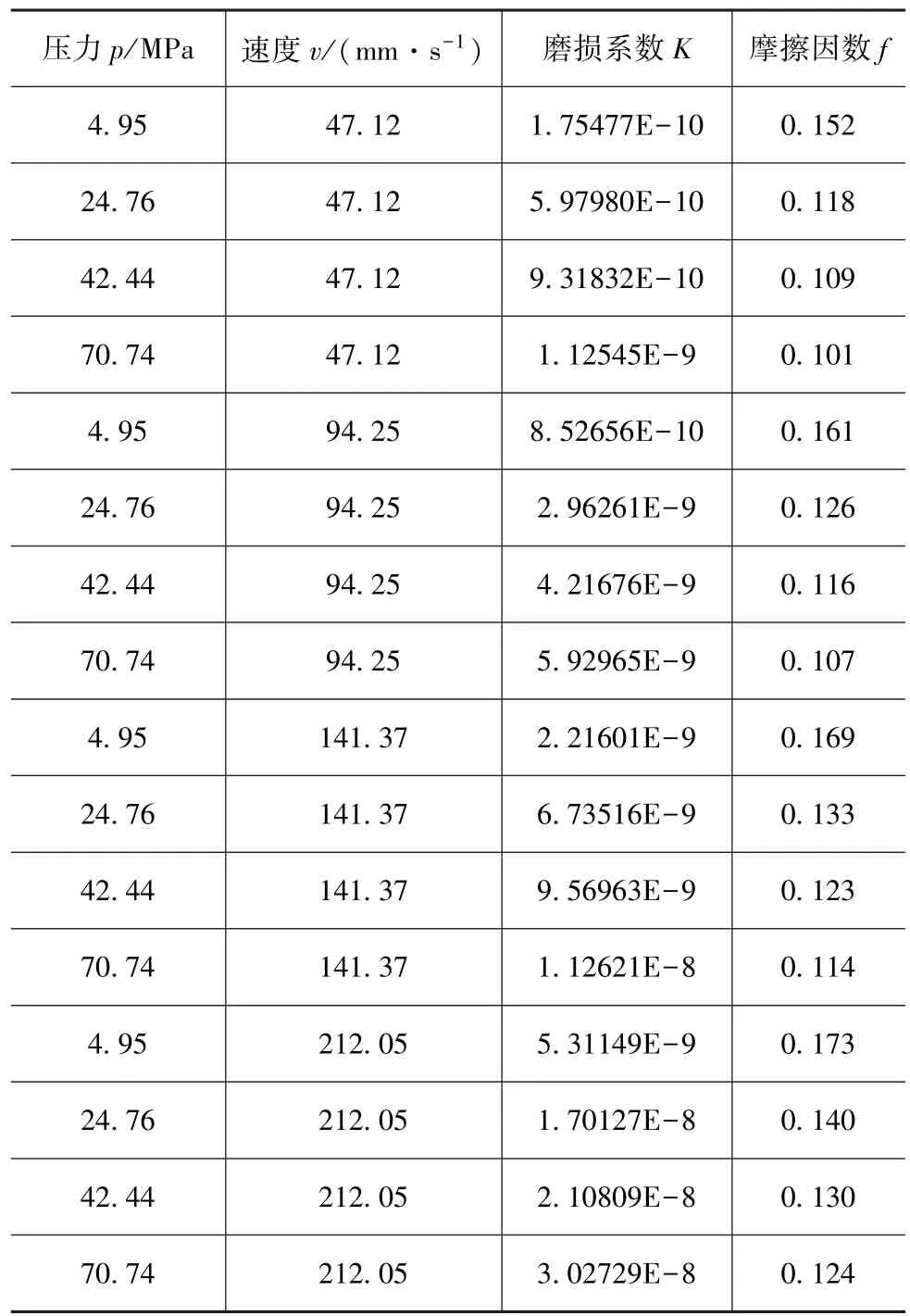
表3 正交实验结果

图5 各压力条件下摩擦因数随速度的变化关系

通过拟合得到不同压力下的摩擦因数随速度变化的公式为

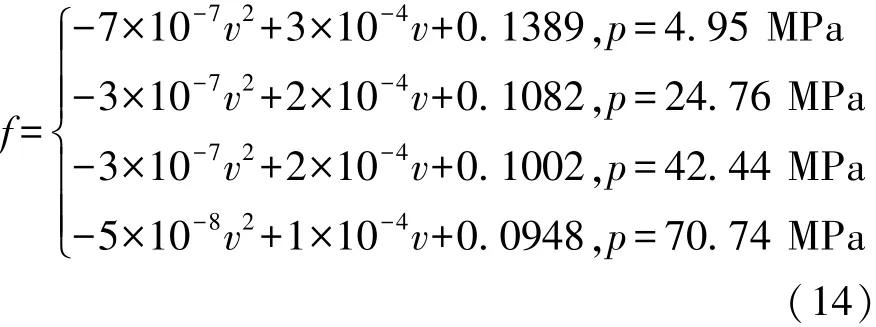
2.5.2 磨损系数

同理，由表2中正交实验所得的各种情况下磨损系数值，利用SPSS软件进行非线性回归分析。由式(6)可得

将表2中压力、速度和测得的磨损系数值代入式(15)线性回归分析式，此外为C1，x和y赋予一个大于0的初始值，并进行分析。

经计算得 C1＝ 6.747×10－13，x＝ 0.685，y＝2.180。因此可得到磨损系数随压力及相对速度变化的动态关系式为

由式(16)可知，相对滑动速度对磨损系数的影响比压力的影响大。

3 模具寿命预测

3.1 冲压仿真计算

如前所述，以某车型左前纵梁加强板为例进行模具磨损预测，该车型加强板材料为DP780，料厚为1.0 mm。

采用LS-DYNA进行冲压仿真，为实现摩擦因数随接触压力和相对滑动速度的连续变化，使用Fortran语言编写仿真子程序，该子程序采用前述拉格朗日插值法，在仿真时基于式(14)进行自动插值计算，求得所需的摩擦因数，从而得到摩擦因数随界面接触压力和相对速度的二维连续变化关系。

3.2 冲压仿真结果对比

将动态摩擦因数所计算的成形仿真结果与工程上将摩擦因数设定为恒定值0.15的仿真结果进行对比，图6所示为成形后零件上两点的厚度对比。

图7为修边冲孔后的零件，对零件相应部位进行现场实测，经过多个零件的多次测量，相应位置的厚度平均值分别为0.959和0.954 mm。因此相对于摩擦因数为定值，动态摩擦因数更接近真实成形状态。

图6 采用两种摩擦因数冲压成形后的节点厚度

图7 加工完成的零件

利用LS-DYNA进行冲压仿真后，须将计算所得的节点力文件导入后处理磨损计算程序中进行磨损计算。将式(16)代入式(8)，同时基于式(8)使用Fortran语言编写模具磨损子程序。

此外，因LS-DYNA计算磨损采用布氏硬度，故须将上述洛氏硬度转换为布氏硬度，其它参数如表4所示。

表4 模型参数

Cr12MoV钢材料的模具经渗硼处理耐磨性增加几倍[17]，因而模具单次磨损量非常微小甚至可忽略不计。此外如果每次计算结果都导出进行磨损计算，计算量大，可操作性不强。为简化计算方法，减少工作量，此处将1万次冲压作为一个单位，每进行一次冲压仿真后导出节点力，然后进行1万次的磨损计算，随后将1万次磨损计算的模具几何导出作为新一轮冲压仿真的输入，以此类推直至模具最大磨损量达到最大允许磨损量为止。

图8为运用动态摩擦因数磨损系数法(DF)与恒定摩擦因数磨损系数法(CF)进行磨损仿真所得到凹模的圆角处节点最大磨损深度对比。

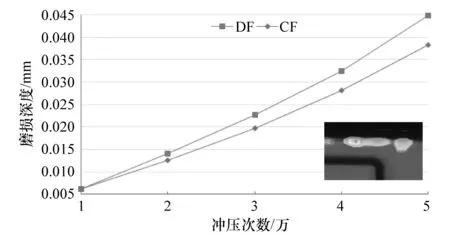
图8 两种方法计算得到的磨损深度对比

3.3 磨损测量与结果对比

图9 为该零件生产现场拉延模具图。模具磨损深度通过车间实测得到，利用激光扫描设备获得该零件拉延模具磨损后的三维实体数据，将扫描得到的数据与模具经CAD设计得到的原始数据同时输入计算机，并以原始数据作为基准来进行数据对比测量。图10为通过高精度扫描仪扫描得到该模具冲压43 252次后型面结果与模具原始几何对比图。由图可知局部区域磨损较大。

图9 左前纵梁加强板拉延模具

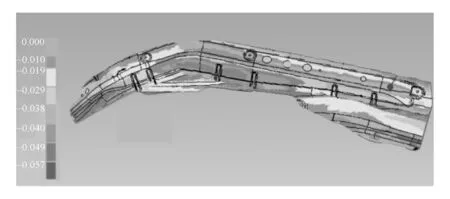
图10 模具型面扫描结果对比

图11 为该模具冲压43 252次后沿凹模圆角(局部图中直线所示方向)局部截面磨损对比。由图可知，经过43 252次冲压后以DF法仿真得到凹模圆角处最大磨损为0.038 7 mm(图中X轴向约5 mm处)，CF法得到该处磨损深度为0.032 5 mm，而该处扫描结果相对原始型面最大距离为0.041 2 mm，由此可见此处精确度提高约15.05%。

图11 冲压43 252次后凹模最大磨损处对比

3.4 模具寿命预测

保证模具质量是保证冲压零件精度的前提与基础，为保证冲压件精度，须在模具磨损一定量后及时对模具进行维修保养，因此在模具使用前期对模具的使用寿命进行合理的预测非常必要。

由上述计算可知，DF法计算模具磨损精度更高，因此以此方法预测模具磨损相对于传统方法更加精确。运用DF法冲压58 924次凹模最大磨损深度为52.76μm，如图12所示。由前面可知，镀层厚度为52.8μm，为防止模具进一步磨损，当模具磨损深度达到镀层厚度时，须进行修模，因此可知该模具的寿命约为5.9万件。

图12 冲压58 924次凹模最大磨损深度

4 结论

(1)冲压成形过程中，板料节点所受的压力及其相对模具的滑动速度不断变化，且二者对磨损系数都有影响，而节点相对滑动速度对磨损系数的影响更大，因此合理控制生产节拍对模具保养具有积极意义。

(2)运用动态的摩擦因数和磨损系数得到的计算方法对本例DP780材料拉延模具进行磨损计算，能明显提高计算精度，在冲压43 252次后精度比传统方法(CF法)提高约15.05%。

(3)运用该方法对某车型左前纵梁加强板拉延模具寿命进行预测，得到模具在表面镀层被破坏之前寿命约为5.9万件，因此在实际生产中应及时对模具表面镀层进行修复，以延长模具使用寿命。