基于时间系数的单点预瞄驾驶员模型分析∗
马芳武,佘 烁,吴 量,王佳伟,史津竹,代 凯
(吉林大学,汽车仿真与控制国家重点实验室,长春 130022)
前言
单点预瞄最优曲率驾驶员模型物理意义清晰,结构简单,计算量小,跟踪精度较高,能很好地反映真实驾驶员的驾驶行为[1]。对于该模型,研究人员提出了多种单点预瞄模型参数辨识的方法[2-5]。为提高轨迹跟踪精度,文献[6]中提出了稳态预瞄动态矫正假说,文献[7]和文献[8]中提出了从误差分析的角度研究确定驾驶员模型参数的解析方法(EAA),在此基础上,文献[9]和文献[10]中提出了位置加方位(position and orientation,PO)预瞄驾驶员模型中参数的确定方法。经过不断研究,即使在非线性区和极限工况下,现有的单点预瞄驾驶员模型都能准确地模拟真实驾驶员的转向操作,跟踪误差小,转向盘转角平顺。
虽然上述单点预瞄驾驶员模型在理论和仿真效果上都很完善,但尚存在以下问题:第一,模型中的输入和反馈量都基于绝对坐标,不能直接用于实际控制,仿真时须对车辆和道路进行精确定位和坐标转换,过程繁杂;第二,通过误差分析法可精确地确定控制参数,但须采集大量实车实验数据进行参数辨识,存在工作量大、辨识结果受工况影响等问题,且这种方法得到的控制参数对各工况的适应性还有待验证。
为此,本文中在单点预瞄驾驶员模型的基础上,对模型部分参数进行重新定义并加以改进,提出一种基于时间系数的单点预瞄驾驶员模型,以弧形道路为例,推导出模型参数的表达式,确定了模型控制参数的计算方法。
1 模型的提出
简化的单点预瞄驾驶员模型如图1所示。图中:v,i,L和 1/s分别为车速、转向系统角传动比、轴距和积分算子;T为预瞄时间;y为车辆实际的横向坐标;f(t)为车辆预期行驶路径上横向坐标与时间的关系;f(t+T)为车辆预期行驶路径上预瞄时间T时刻的横向坐标。f(t+T)为系统的输入,y为系统的输出,T为控制参数,整个控制过程可描述为通过控制预瞄时间T,使系统输出y尽可能跟踪预期行驶轨迹f(t),即y与f(t)之差尽可能小。
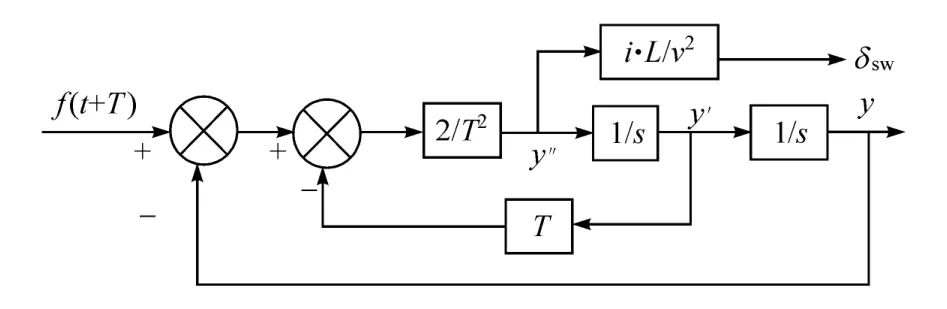
图1 简化的单点预瞄驾驶员模型

图2 新的单点预瞄驾驶员模型
在图1所示的单点预瞄模型基础上,本文中对其进行重新定义,增加误差反馈系数K;由于车辆相对于道路的侧向速度在实际过程中无法直接获取,其相对于预瞄时间的反馈实际上无法实现,所以删掉相对速度对预瞄时间的反馈,得到如图2所示的模型。如何变化,系统的输出ye尽可能接近零。整个系统表示的不再是轨迹跟踪问题,而是对扰动的抑制问题,将预瞄作用看成是外界的扰动,即无论预瞄点处的车辆质心横向位置误差多大,都要求当前的质心横向位置误差始终为零。可以看出,与之前模型不同的是,系统的输入和中间反馈量都是车辆坐标系下的相对量,表示的是车辆与道路中心线的相对位置关系。
以圆形弯道为例,对该模型进行如下分析。
在一定弯道半径R和纵向车速v的情况下,预瞄时间为T时,前方道路预瞄误差可分为3部分,如图3所示:由道路曲率所产生的预瞄误差fyr,即车辆质心位于车道中心线上、车辆坐标系的x轴与道路切线平行时的预瞄误差;由偏航角ϕe产生的预瞄误差fya;车辆当前的质心横向位置误差fyc。车辆预瞄点处的预瞄误差fy等于由道路曲率产生的预瞄误差fyr减去车辆航向角产生的预瞄误差fya和当前车辆质心横向位置误差fyc:

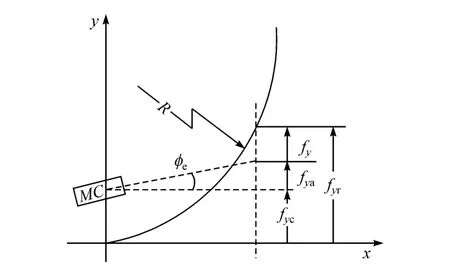
图3 车辆预瞄误差
对于圆形弯道,道路轨迹的横向坐标与时间的关系如图4所示,由道路曲率产生的预瞄误差为
图中:y″为预期的车辆横向加速度,ye″,ye′和ye分别为车辆相对于道路中心线的横向加速度、横向速度和横向位置或偏差;fe(t+T)为车辆纵轴上预瞄时间T时刻对应的预瞄点与道路中心线的横向距离,即横向预瞄误差;K为当前横向误差的反馈系数;ay(t)为跟踪当前道路中心线所需要的侧向加速度,可根据车速和弯道半径计算出来。fe(t+T)为系统的输入,ye为系统的输出,T和K为控制参数,整个控制过程可描述为通过控制预瞄时间T和反馈系数K,使得无论系统的输入fe(t+T)

图4 圆形道路下道路曲率预瞄误差fy r示意图
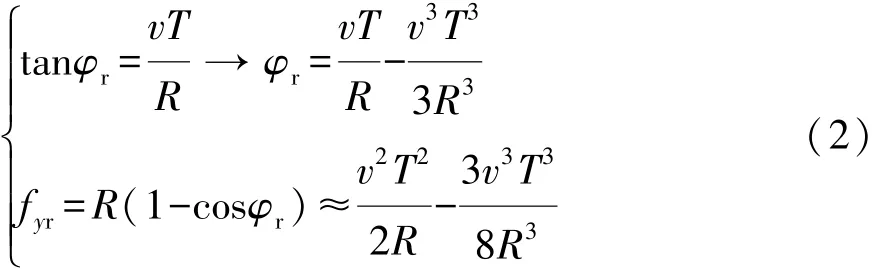
以圆形弯道作为输入对图2所示模型进一步具体化,考虑侧向加速度和横摆角速度对前轮转角的稳态增益,得到图5所示模型,图中H为不足转向系数。为便于后续分析,只考虑输出对输入的响应,故去掉转向盘转角分支,同时将v/Rs和v2/R简化到输入端,得到图6和式(3)。
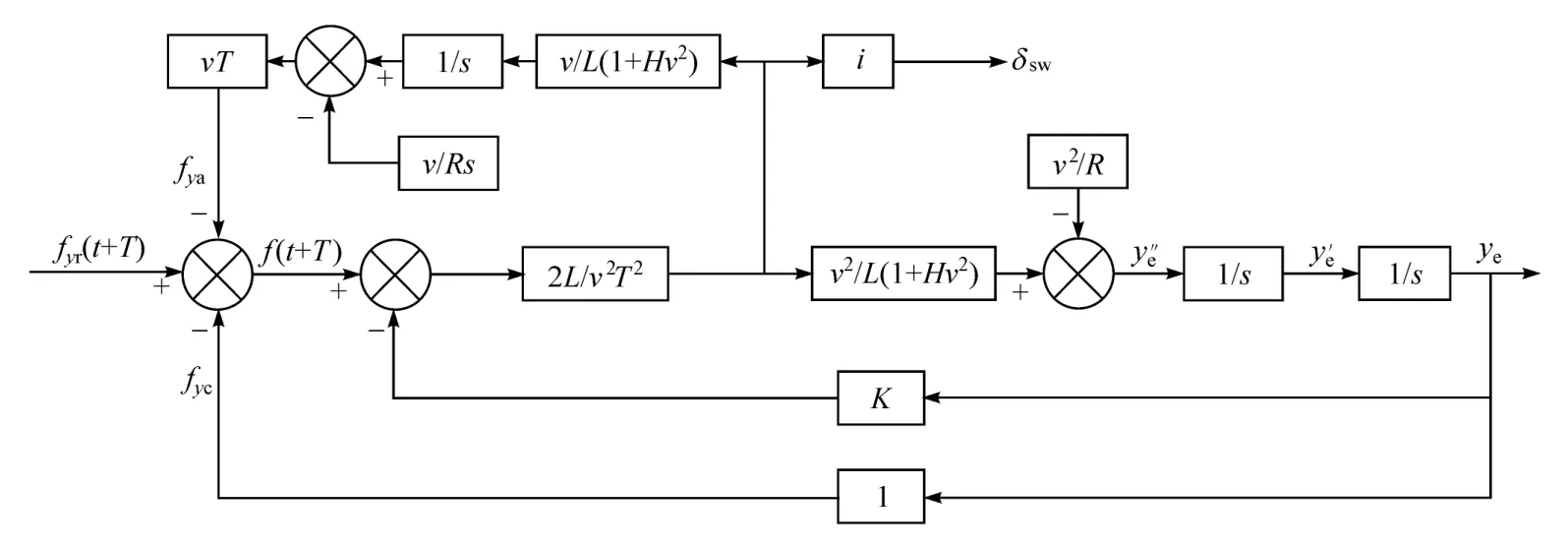
图5 圆形道路下的单点预瞄驾驶员模型
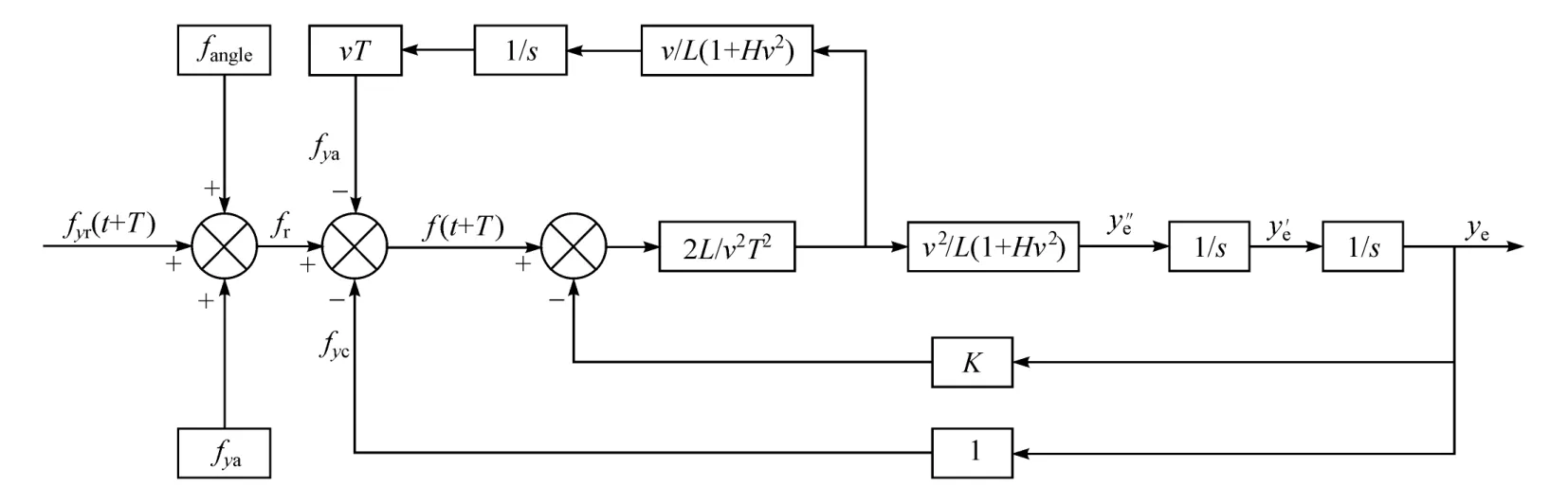
图6 简化之后的圆形道路下单点预瞄驾驶员模型
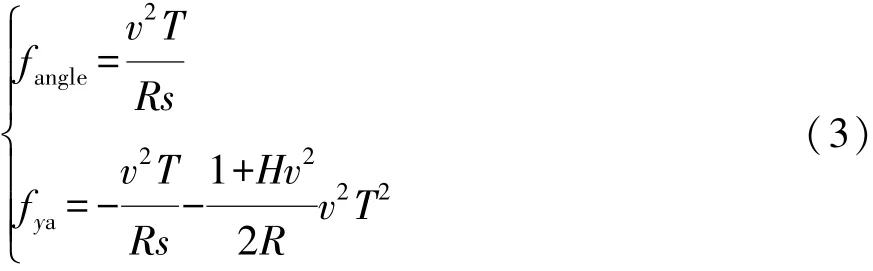
系统的等效输入如式(4)所示,为两个阶跃信号的组合。图6所示系统的分析结果如式(5)所示,依次为传递函数、系统固有频率、阻尼比和稳态误差。从式(5)可以看出:稳态误差与所需侧向加速度符号相反,说明车辆一直偏向于弯道外侧行驶;增加K可减小稳态误差,但会提高系统的振动频率;增大T会增大稳态误差,但可减小振动频率;车速升高,稳态误差增大,振动频率减小;所需侧向加速度增大,稳态误差也会增大。

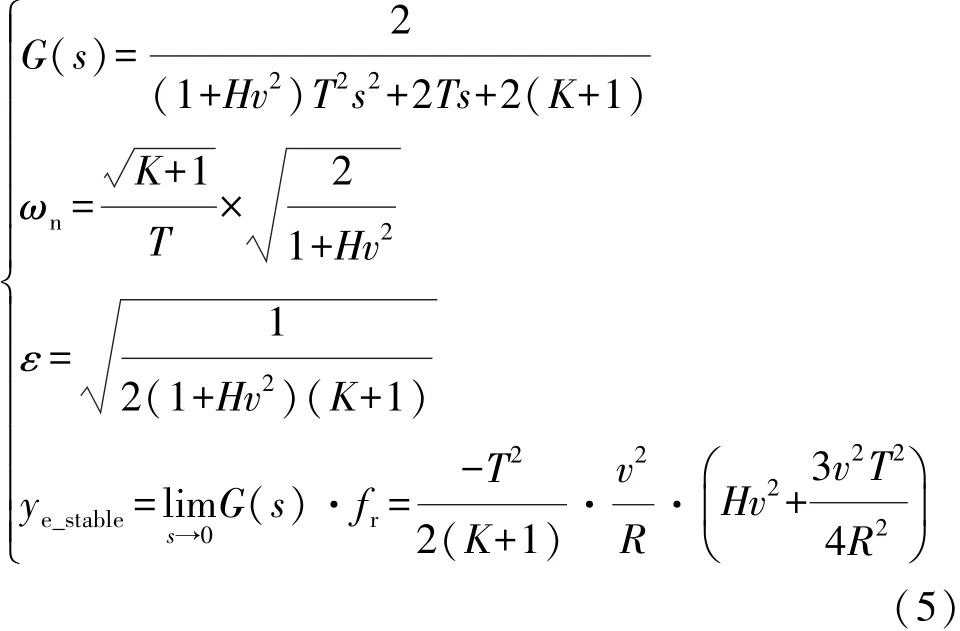
2 模型的完善
根据以上分析,通过调节预瞄时间T和反馈系数K可控制横向位置误差和转向盘转角的平顺性,由式(5)可以得到式(6),可以看出:系统固有频率的平方与车辆稳态横向位置误差的乘积、与所需侧向加速度成正比,且随着车速的升高和预瞄时间的增加而增大,当侧向加速度较大时,无法兼顾跟踪误差和转向盘转角控制的平顺性。

产生上述问题的原因分析如下:在转向开始时计算出的转向盘转角偏小,导致车辆偏向于弯道外侧行驶,在误差达到一定值时通过反馈系数K使稳定时的转向盘转角与当前弯道半径和车速相适应。直观地分析,可通过增加预瞄时间T使fyr增加(进而fr增加),使得算出的转向盘转角增加,但从式(7)可以看出(没有考虑偏航角导致的预瞄误差),改变T时,等式左右两侧均变化,无法直接调节稳态误差,最终还是通过ye增加来平衡等式。

根据以上分析,问题的根本在于计算出的侧向加速度偏小,原因是侧向加速时间偏长,即问题出在侧向加速时间T(式(7))与纵向预瞄时间完全相等,没有解耦。从物理意义上看,这两者没有必然联系,因而也没必要完全相同,基于此,在图6所示模型基础上,增设表征侧向加速时间与纵向预瞄时间的比例关系系数F,得到图7所示的新模型。
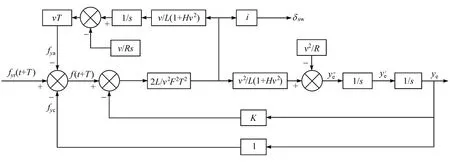
图7 二次改进后的圆形道路下单点预瞄驾驶员模型
按照上节相同的分析方法,得到式(8)和式(9),相对于式(5),可以看出:在预瞄时间T一定的情况下,通过合理设计时间系数F,可使系统的稳态误差为零;同时,由固有频率和阻尼比的表达式看出,可通过控制反馈系数K来调节系统的频率特性。因此采用如下设计方法,可在保证转向盘转角平顺性的同时,实现给定任意轨迹的无差跟踪:首先,根据弯道半径大小对视野和传感器有限感知范围的约束,确定预瞄距离,进而确定预瞄时间T;然后,根据稳态误差表达式确定零稳态误差时的时间系数F(式(10));最后,根据系统的超调量和调节时间确定阻尼比和固有频率,进而确定反馈系数K。

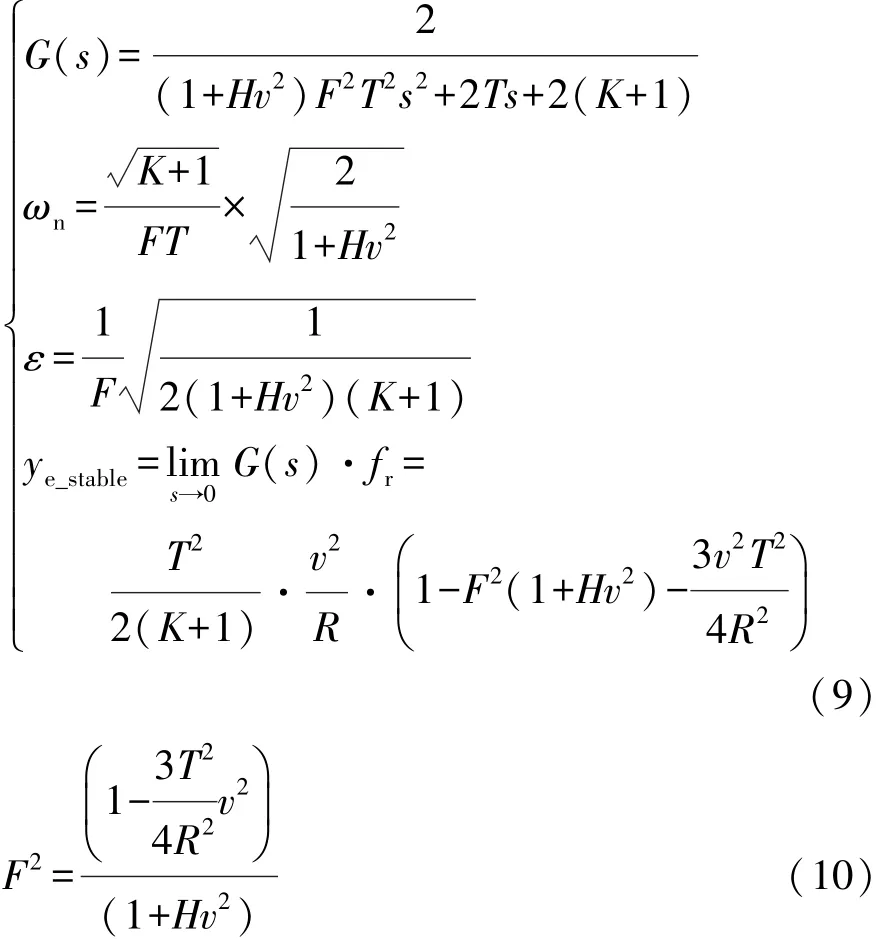
3 模型的验证
在Simulink中搭建系统的简化模型进行仿真,设置弯道半径为500 m,车速为90 km/h,车辆轴距为2.91 m,不足转向系数为7.715×10-4(在CarSim中通过稳态圆周实验测得对应侧向加速度下的不足转向梯度),进行两组仿真:仿真一,预瞄时间T=1 s和反馈系数K=2不变,时间系数F分别为1,0.9,0.821(按式(10)算出的值)和 0.6,以对比时间系数F对控制效果的影响;仿真二,预瞄时间T=1 s和时间系数F=0.821不变,反馈系数K分别为0,1和2,以对比反馈系数K对控制效果的影响。
仿真一的结果如图8(a)和图8(b)所示,分析如下。
(1)时间系数等于1时,横向位置存在稳态误差,约为-0.1 m,偏向于弯道外侧行驶(横向位置误差与侧向加速度符号相反,为弯道外侧);F取0.9时,横向位置误差约为-0.04 m,偏向于弯道外侧行驶;在F取0.6时,横向位置误差约为0.1 m,车辆偏向于弯道内侧行驶。由此可见:随着时间系数F的减小,车辆的稳态横向位置逐渐由弯道外侧向弯道内侧变化,说明可通过F调节车辆在车道中的横向位置。
(2)当F取0.821时,车辆的稳态横向位置误差接近于零,转向盘转角波动较小,说明式(10)算出的F是准确的。因此,可总结如下:在一定车速和弯道半径下,针对每个T,都存在一个由式(10)确定的F,可精确实现给定轨迹的跟踪,小于此值,车辆偏向于弯道内侧行驶,大于此值,车辆偏向于弯道外侧行驶。
仿真二的结果如图8(c)和图8(d)所示,分析如下。
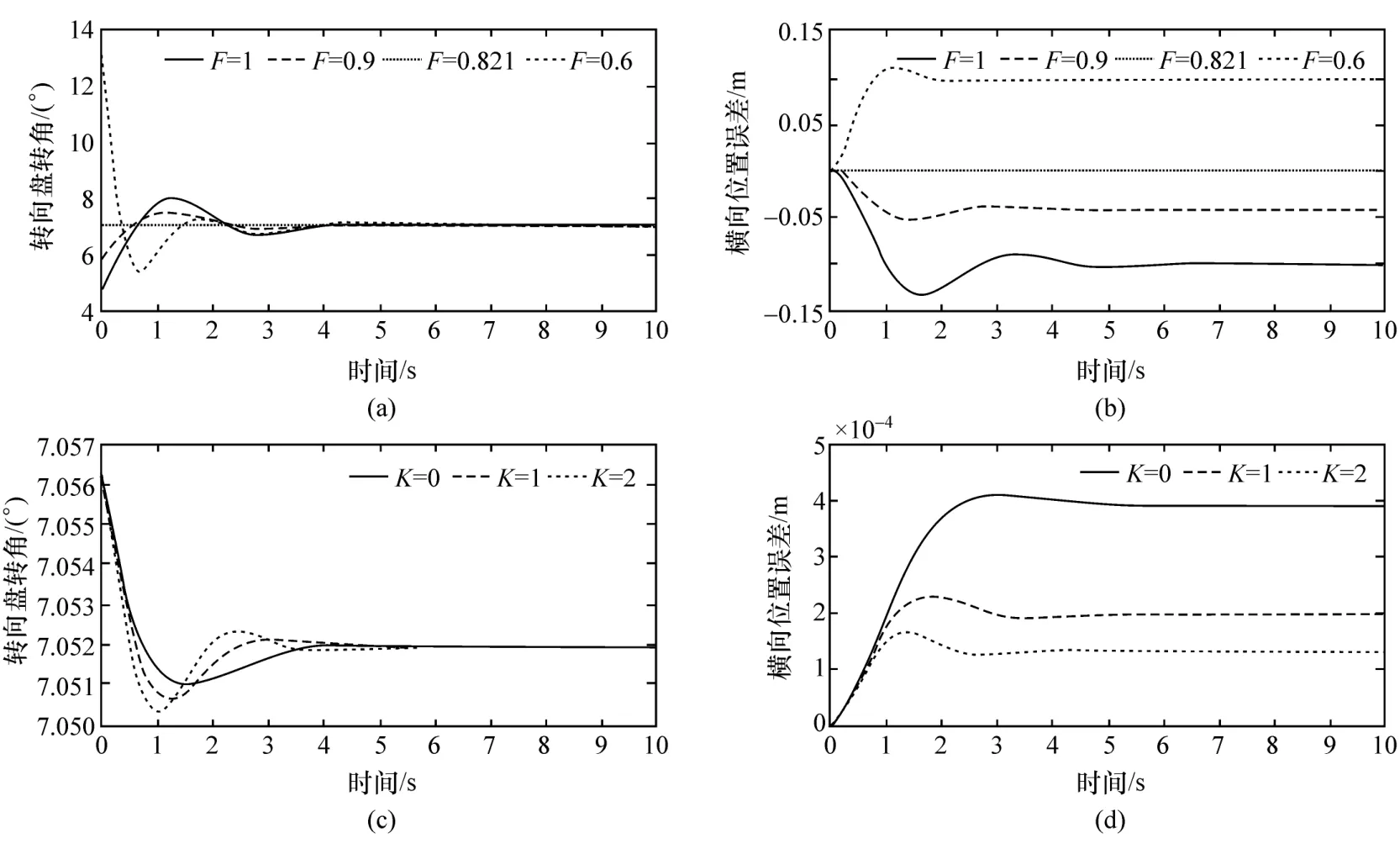
图8 F和K对控制效果的影响(Simulink仿真)
增大K会增加转向盘转角的振荡频率,而减小横向位置的稳态误差。当F取值比较准确时,横向位置稳态误差接近于零,此时增大K以继续减小横向位置误差已无意义,但可通过调节K控制系统的振动频率或阻尼比。
为验证模型的准确性,按照上述条件进行了CarSim-Simulink联合仿真,结果如图9所示。由于CarSim中的车辆模型较精确,有动态特性,图8与图9结果中:转向盘转角的幅值有所差异,两者的振动频率特性相似;横向位置误差的动态特性有所不同,但稳态误差高度吻合。
4 结论
本文中在单点预瞄驾驶员模型的基础上,提出了基于时间系数的单点预瞄驾驶员模型,将输出对输入的跟随问题转化成了输出对输入的扰动抑制问题,分析了控制参数对控制效果的影响。为消除稳态误差,将纵向预瞄时间和侧向加速时间进行解耦。通过理论分析和仿真实验,得到如下结论。
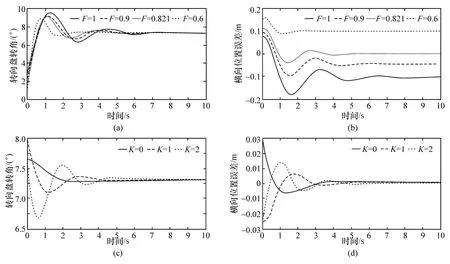
图9 F和K对控制效果的影响(CarSim-Simulink联合仿真)
(1)在工况和纵向预瞄时间一定的情况下,通过调节时间系数,可控制车辆在车道中的横向位置,存在临界时间系数,使车辆能零稳态误差地跟随给定的弧形弯道。当小于此临界值时,车辆偏向于弯道内侧行驶,当大于此临界值时,车辆偏向于弯道外侧行驶。
(2)在工况、纵向预瞄时间和时间系数一定的情况下,通过控制反馈系数,可控制系统的频率特性和稳态误差。增大反馈系数,系统的振动频率增加,稳态误差减小。

