浅谈常数“1”在均值不等式中的巧用

北京市北京师范大学出版集团(100875) 岳昌庆

我们知道：若a,b ∈R+，则a+b≥(当且仅当a=b时，取等号)

(1)当ab为定值m时，a+b的最小值为此时

(2)当a+b为 定 值l时，ab的 最 大 值 为此 时

以上为均值不等式及其应用的相关结论，形象地、简单地说就是“一正二定三相等”.本文仅只谈均值不等式在高考真题中的一个有趣的应用.

例1(2007年高考山东卷理科第16 题(4 分填空压轴题))函数y=loga(x+3)-1(a＞0 且a1)的图像恒过定点A，若点A在直线mx+ny+1=0 上，其中mn＞0，则的最小值为____.

简解由已知可得A(-2,-1)，所以2m+n=1，又mn＞0，故m＞0,n＞0，(当且仅当即时，取等号).

评注(1)本题巧妙利用已知条件1=2m+n代入目标函数并将该目标函数化成关于的均值不等式.(2)本题也可用换元法设则关于m,n的二元目标函数本质上就变为关于t的一元函数(t＞0)，于是可用求导的方法得到f(t)的最小值.以下各例不再一一提及.

例2(2012年高考浙江卷文科第9 题(5 分))若正数x,y满足x+3y=5xy，则3x+4y的最小值是( ).

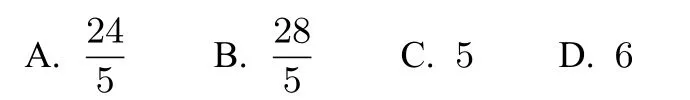
简解由已知可得则(当且仅当即时，取等号)，故选C.

评注(1)将已知条件化为后，由于常数余则同例1.(2)本质上，例2 与例1 的已知条件及目标函数似是“互逆”的，且均有最小值.

例3(2013年高考天津卷理科第14 题5 分压轴题)设a+b=2，b＞0，则当a=____时，取得最小值.

简解由已知可得b=2- a＞0，故a＜2.所以(当且仅当即b=2|a|即a+2|a|=2 时，取等号)，即a=-2 时，取得最小值

评注(1)由于常数及已知条件a+b=2，代入中，余下同例1.(2)本质上，是一个常数或

例4在4×○+9×△=60 的○△中，分别填入1 个自然数，使它们的倒数和最小，应分别填上____和____.

简解设○=x,△=y，则已知条件为4x+9y=60，目标函数为(当且仅当即x=6=○，y=4=△时，取等号).

评注(1)当我们用代数的思想设元来解决这个问题时，本质上同例1.(2)由于常数及已知条件4x+9y=60，代入目标函数即可得.

这种类型的题目频频出现在高考真题中，既有其知识点考查的必要性，也有其数学思想方法考查的趣味性.

作业1(2007年高考山东卷文科第14 题(4 分))函数y=a1-x(a＞0，a1)的图像恒过定点A，若点A在直线mx+ny-1=0(mn＞0)上，则的最小值为____.

作业2(2004年高考重庆卷文科第14 题(5 分))已知则xy的最小值是____.

作业3(2013年高考天津卷文科第14 题(5 分压轴题))设a+b=2，b＞0，则的最小值为____.