密闭空间氡气浓度变化规律与估算方法研究

林 意，张庆贤，王 玥，王 猛，张 建，黄 健，张懋轩

(成都理工大学 核技术与自动化工程学院，四川 成都 610059)

氡及其子体普遍存在于土壤、空气中，是自然界三个天然放射性系中唯一的气态元素。地壳中铀系、钍系和锕系均连续向四周扩散氡气，使土壤、水和空气中富含氡气，因而研究氡气在空间中的累积过程具有重要意义[1]。

目前，国内外研究者对氡气反扩散系数与氡气浓度变化规律开展了诸多研究。例如，李志强[2-3]研究了累积法测量介质表面氡析出时，泄漏和反扩散对测量结果的影响，并提出局部静态法固有的泄漏与反扩散影响的消除方法；赵剑锟等[4]分析了反扩散效应对地震氡迁移的影响并建立了修正模型；Muoz等[5]考虑了土壤以及建筑材料的物理参数，建立二维有限元模型，该模型可以通过不同的建筑物边界条件来预测建筑物密闭空间内氡气浓度；Singh等[6]利用一维模型推导出三维半经验模型用于预测室内氡气浓度。目前研究中,对密闭空间中氡气反扩散研究较少，刘小松等[7]的研究表明，在密闭空间中氡气浓度分析过程需对氡气反扩散影响进行修正。因此，本研究通过密闭空间氡气浓度测量实验，分析氡气反扩散系数与氡气浓度之间的关系，采用微分方程对密闭空间中氡气浓度进行建模，拟为密闭空间中氡气浓度变化预测提供参考。

1 理论基础

氡在土壤介质中的迁移是一个复杂多向的物理过程，受到多因素的影响，土壤氡气析出率可表示为[8]：

(1)

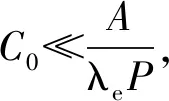
(2)

式中：F为土壤氡气析出率，Bq·m-2·s-1；P表示土壤总孔隙度，无量纲；De为有效扩散系数，指氡气在介质孔隙空间中的扩散系数，m2·s-1；A为土壤氡的产生率，Bq·m-3；λe为衰变常数，2.16×10-6s-1；C0为介质孔隙中的氡浓度，Bq·m-3；ρ为土壤容重，kg·m-3；E为土壤射气系数，无量纲；R为土壤中Ra的活度，Bq·kg-1。其中，土壤射气系数、总孔隙度等参数难以直接测定，理论上计算氡气析出率难度较大。

若假定氡气析出率为常数，密闭空间中氡气浓度为[9]：

(3)

随着时间增加，氡气在密闭空间的浓度升高，氡气反扩散对氡气浓度的影响增强。若考虑氡气反扩散的影响，氡气浓度变化微分方程可表示为[9]：

(4)

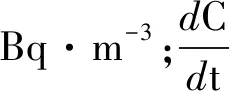
2 测量方法

采用等时间间隔测量法测量氡气析出率[10]。本次实验地表土质为原生粘土，测量仪器选择FD216环境测氡仪。测量装置原理图与实物图示于图1。

集氡罩用亚克力板制作，板厚7 mm，集氡罩体积为98 cm×98 cm×97 cm。测氡仪的进气口与排气口分别与集氡罩的排气口和进气口相接，实现气体的循环。为排除f值中泄漏率的影响，需要保证装置的气密性，因此集氡罩安装在深度为20 cm的槽内，并用粘土密封周边。传感器安置在集氡罩内，实时测量土壤和集氡罩内温度、湿度等参数。实验分别于2015年9月(第1次实验)和2015年11月(第2次实验)进行，根据氡气析出率快速测量方法[11]，设定实验时间为62 h，测量间隔为2 h，测量时间为30 min。

3 分析与讨论

3.1 氡气反扩散系数

实验中前2次测量的氡气浓度较小，式(4)

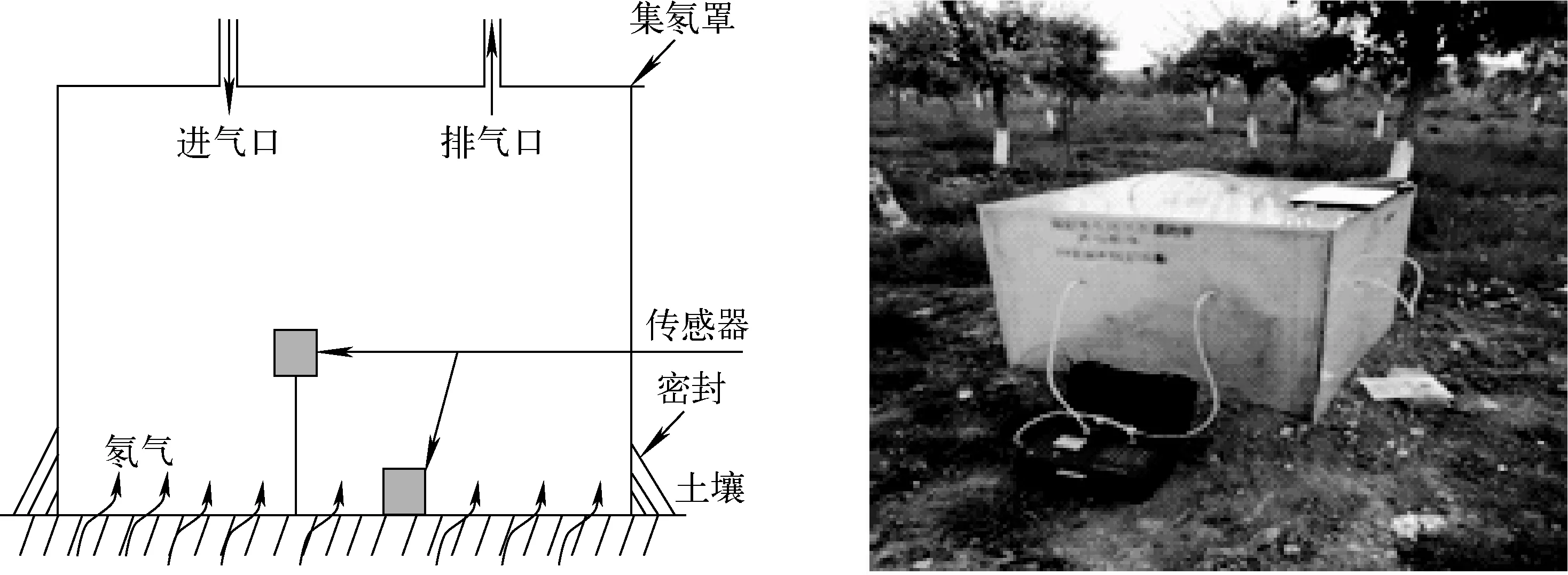
图1 实验装置图和实物图Fig.1 Experimental diagram and device

中fC可近似为0，由式(4)可求得氡气析出率。

表1 实验数据计算氡气析出率结果Table 1 Results of radon exhalation rate from experimental data

不考虑氡气反扩散影响时，氡气的理论计算浓度与实测浓度之间的关系示于图2。由图2结果可知，两者变化趋势差异明显。

(5)

式中参数与式(4)相同，F取表1中的平均值。利用分析方法[2]，求得f值同时间和氡气浓度之间的关系示于图3和图4。

由图3和图4可以看出，f值随时间和氡气浓度在一定范围内波动变化。f值的平均值及统计分析结果(一倍、两倍、三倍均方差内)列于表2。

两次实验得到的f值的平均值分别为0.015 7和0.024 1，标准差分别为0.007 3和0.013 8。由表2结果可以看出，f值的波动较大。将温度与f值进行拟合分析，得到两次实验的拟合系数均小于0.1，因此难以确定温度与f值之间的相关性，对于f值波动影响因素，还有待进一步实验和分析。

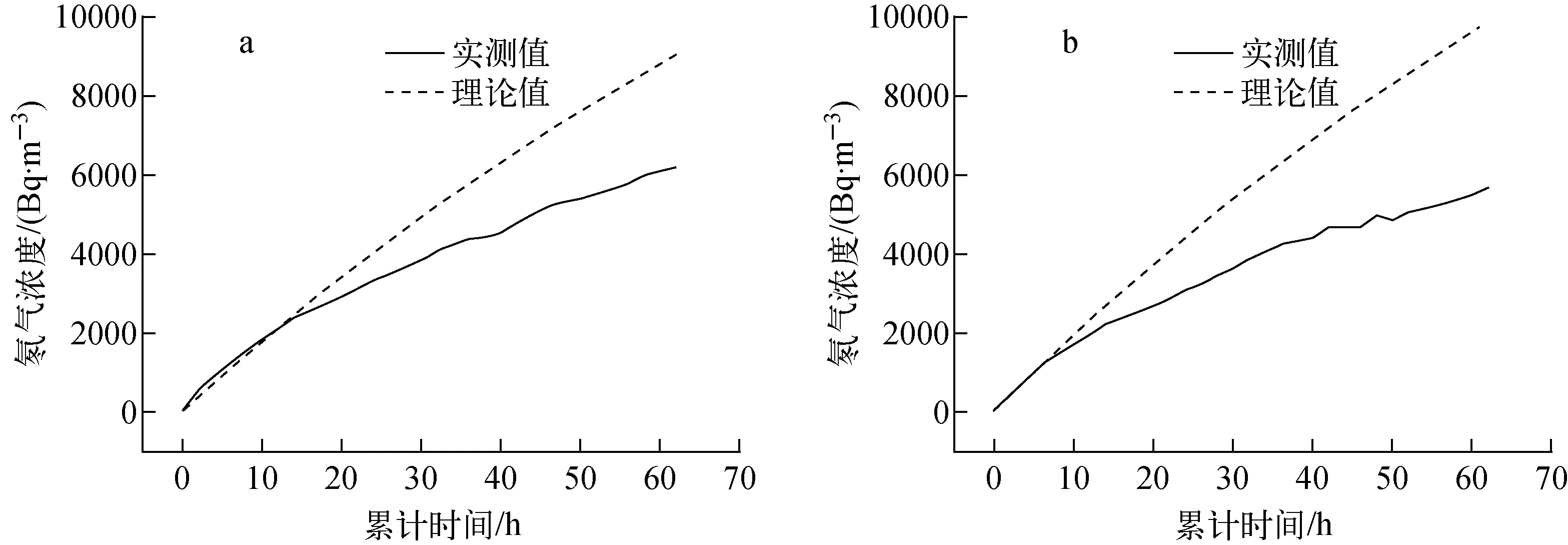
a——第一次实验 ； b——第二次实验图2 不考虑氡气反扩散影响时氡气浓度理论曲线与实测氡气浓度变化曲线a——First experiment；b——Second experimentFig.2 The theoretical curves of radon concentration without considering the effect of back-diffusion and the experimental curve

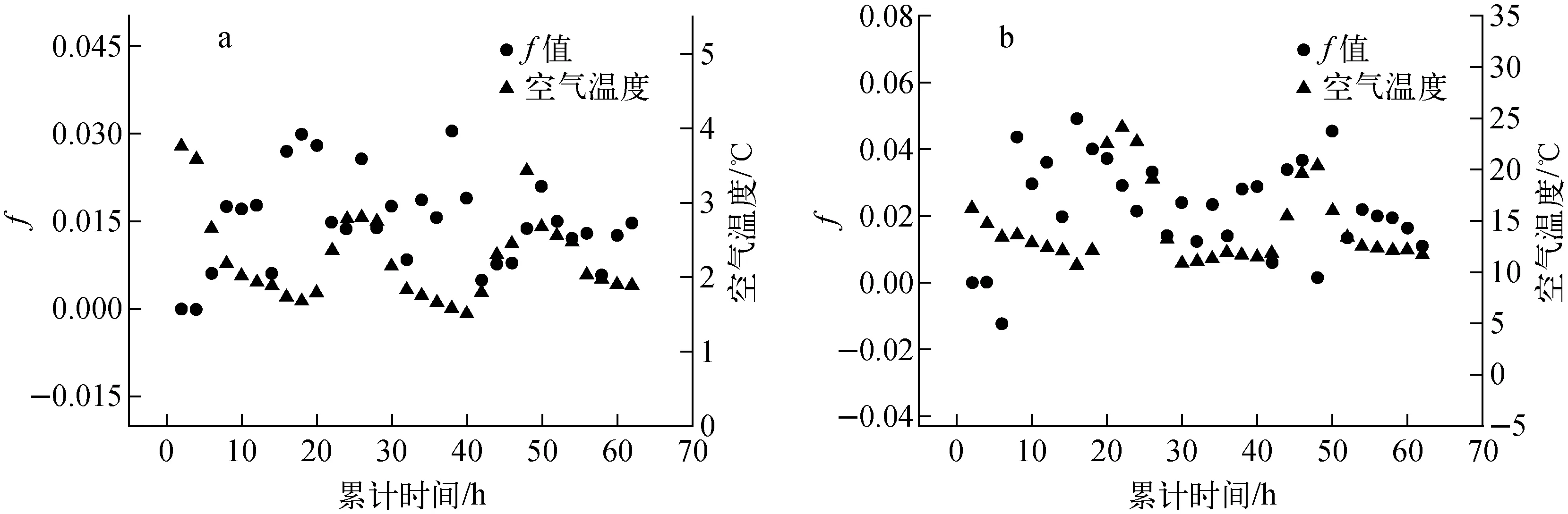
a——第一次实验；b——第二次实验图3 氡气反扩散系数f值、温度随时间变化图a——First experiment；b——Second experimentFig.3 The relationship between back-diffusion coefficients、temperature and time

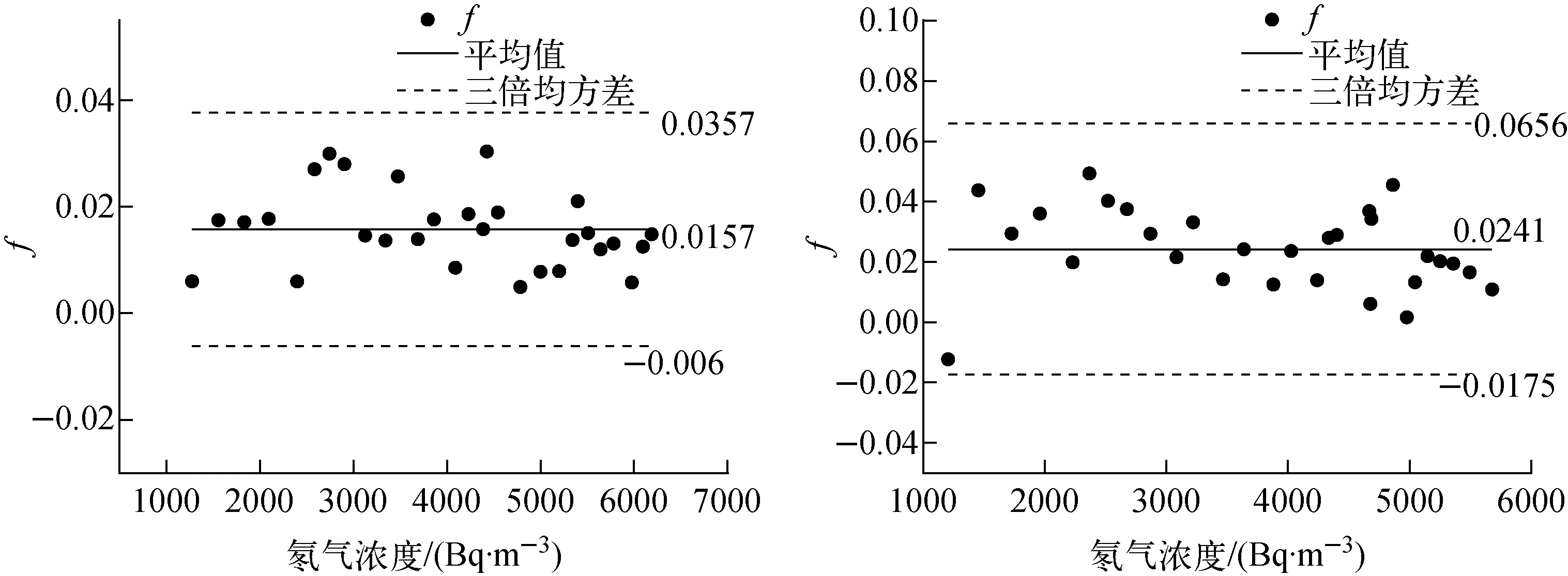
a——第一次实验；b——第二次实验图4 氡气反扩散系数f值与浓度的关系图a——First experiment；b——Second experimentFig.4 The relationship between the radon concentration and back-diffusion

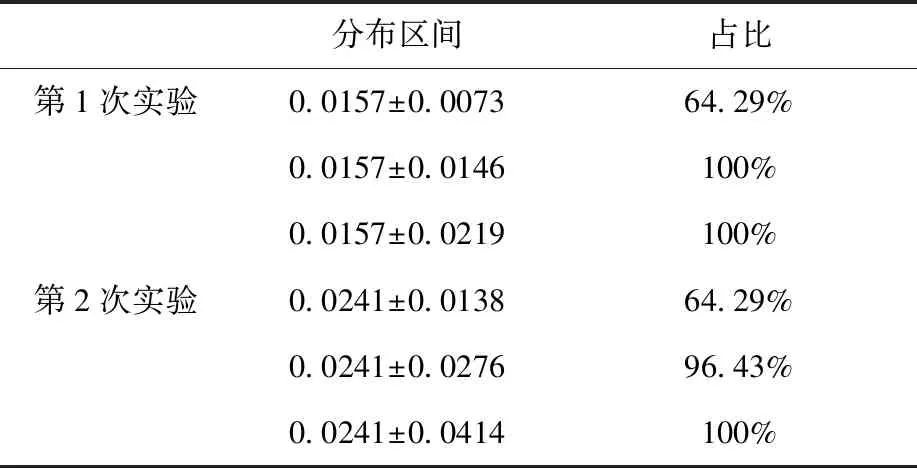
表2 氡气反扩散系数f值统计结果Table 2 The statistical result of back-diffusion coefficient

3.2 密闭空间氡气浓度预测

假设测量时间间隔为t，每个测量时间点Ti对应的氡气浓度值为Ci，且初始浓度C0很低，则对密闭空间氡气浓度进行预测计算，步骤如下：

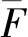
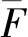
(6)

式中参数与式(4)相同。通过以上方法，对两次实验密闭空间内氡气浓度进行预测，结果示于图5。模拟值与实测值之间的相对误差Δ示于图6。Δ计算公式为：

(7)

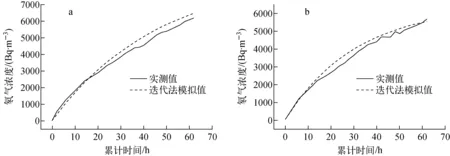
a——第一次实验；b——第二次实验图5 考虑氡气反扩散系数的氡气浓度模拟曲线与实测曲线a——First experiment；b——Second experimentFig.5 The simulated curve which considering the coefficient of back-diffusion and the experimental curve

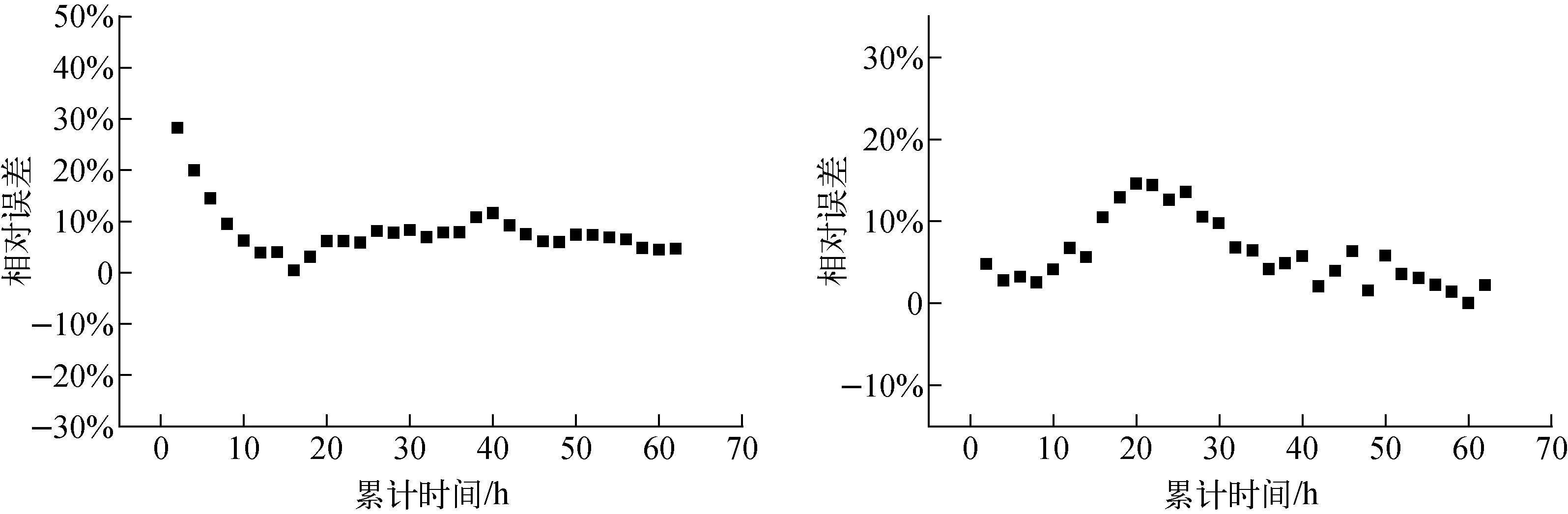
a——第一次实验；b——第二次实验图6 模拟浓度与实测结果的误差图a——First experiment；b——Second experimentFig.6 The relative error of simulated and experimental radon concentration

由图5结果可知，模拟曲线与实际测量曲线非常接近，且模拟的误差随着时间增加而减小。图6中第一次实验模拟值平均误差为8.06%，最大误差为28.38%；第二次实验模拟值平均误差为6.13%，最大误差为14.65%。由此表明，考虑了氡气反扩散影响后，密闭空间中氡气浓度可应用理论方程较好的进行计算和预测。

4 结论

通过理论计算和实验，分析了密闭空间中氡气浓度变化规律和氡气反扩散系数的影响。将氡气反扩散系数看作常数用于氡气浓度计算的迭代方程，实现对密闭空间中氡气浓度理论计算，所得计算结果与实测结果接近，两者最大误差均小于30%，平均误差均小于10%。采用理论计算和迭代的方法，可以预测密闭空间中氡气浓度。