一种新型分数阶Tikhonov正则化载荷重构技术及应用

王能建， 任春平， 刘春生

(1. 哈尔滨工程大学 机电工程学院，哈尔滨 150001； 2. 黑龙江科技大学，哈尔滨 150022)

反问题广泛存在于国防军事、航空、航海、矿山冶金及机械工程等领域。实际工程应用中，如载荷重构、系统参数识别等都属于反问题范畴[1-2]。但在处理反问题的过程中由于系统或参数矩阵存在病态性，导致很难得到准确解。因此，探寻一种稳定求解反问题方法是国内外学者不断探索的重要课题，尽管许多学者作出了重要的贡献，但目前还没有完全成熟的理论研究技术。

整数阶Tikhonov正则化重构技术，作为处理反问题的一种间接手段，被许多学者所探究[3]。Choi等[4-5]研究整数阶Tikhonov正则化方法，分析响应数据中噪声对重构结果的影响。郭荣等[6]结合了整数阶Tikhonov正则化与奇异值分解的方法，改善了结构随机载荷重构精度。张磊等[7]研究了总体最小二乘整数阶Tikhonov正则化技术对载荷重构的影响。常晓通等[8]探究了基于 Green函数的整数阶Tikhonov正则化载荷重构方法。孙兴盛等[9]结合矩阵摄动与整数阶Tikhonov正则化方法对随机结构进行了动态载荷重构研究。彭凡等[10]采用截断奇异值分解Tikhonov正则化方法，对结构冲击载荷进行了重构研究。虽然整数阶Tikhonov正则化重构技术已被许多专家学者研究讨论并得到了很多有价值的结论，但是其仍然存在着某些技术难点与不足，尤其是在工程实际应用领域，该重构技术目前国内还没有得到成熟的应用。

王能建等[11]提出了路径规划与整数阶Tikhonov正则化相结合的算法，并应用到了甲板上舰载机牵引系统参数重构中。刘春生等[12]将整数阶Tikhonov正则化技术应用到截割煤岩随机载荷重构中，验证了算法的可行性，但重构的精度不够理想。Liu等[13]将整数阶Tikhonov正则化技术与小波变换相结合，应用到矿山机械中，解决了该领域的许多重要问题。刘春生等[14]中已经提到过关于分数阶微积分理论与正则化技术相结合的分数阶正则化技术在矿山机械领域的应用，这将会是未来重要的研究课题方向。然而，目前国内关于分数阶正则化技术研究报道较少，且其具体工程应用还不够成熟和完善。

本文在以前研究工作基础上，针对上述重构技术在实际工程应用过程中所存在的不足，如系数矩阵病态性、抗噪弱、正则解平滑等问题，提出一种新型分数阶 Tikhonov正则化载荷重构技术，其方法的技术路线为将动载荷在时域表示为一系列核函数的叠加，并且结构(系统)的测量响应表示为输入载荷和核函数响应之间的卷积分形式，由于核函数响应矩阵的病态性和具有噪声污染的测量响应，通过离散可以将卷积方程转化为线性方程组形式，对其进行反求。然后利用本文提出的技术方法将反求过程转化为一类无约束优化问题，并采用超记忆梯度法求解目标函数，最终获得与真实载荷在精度上相匹配的识别载荷。

所提出的技术与以前的研究工作相比具有重要的改进意义。①所提出的技术能够克服病态问题的不适定性； ②将处理反问题的过程转化为无约束的优化问题，采用超记忆梯度法处理目标函数，提高求解速度；③所提出的技术方法不需要任何关于载荷重构模型的先验信息；④通过工程应用例子，验证了所提出技术的实用性和稳定性。

本文的结构具体安排如下：第一部分，载荷重构模型的描述；第二部分，一种新型分数阶 Tikhonov正则化载荷重构技术被提出；第三部分，所提出技术在截齿截割煤岩载荷重构中的应用；第四部分，重要的结论被给出。

1 模型描述

动态载荷识别问题是结构动力学中一类重要的反问题，在实际工程问题中，外部动态载荷信息在结构(系统)动力学分析、健康监测、强度环境校核等领域扮演着非常重要的角色。然而在很多情况下，由于经济成本或者复杂环境等原因，直接测量工程结构所受动态载荷往往非常困难甚至是不可能的。然而，结构响应往往比较容易获得，根据时域方法理论建立系统的载荷识别模型，通过核函数方法建立正问题方程，将动载荷利用一系列核函数相叠加的方式表示，结构的测量响应就可表示为输入载荷和核函数响应之间的卷积分形式，即其模型可用第一类弗雷德霍姆(Fredholm)方程表示[15]

(1)

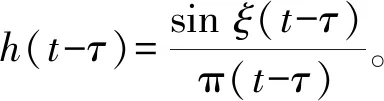
测量结构响应y(t)为含有噪声e(t)的测量值，其可用下述表达式

yδ(t)=y(t)+e(t)

因此，式(1)可用式(2)代替

(2)

基于矩形公式，对式(3)进行离散化处理

(3)

令yδ,k=yδ(tk)；zi=z(τi)；hk-i=h(tk-τi)。z=(z1,z2,…,zn-1,zn)T;Yδ=(yδ,1,yδ,2,…,yδ,n-1,yδ,n)T；A=(ak-i)n×n。

其中， 当y≠i时

当k=i时

AZ=Yδ

(4)

模型式(4)表明结构(系统)所受的动载荷是通过其测量响应和结构的特性来识别的。但是，载荷识别问题作为结构(系统)动力学的第2类逆问题，其具有不适定性，因此找到一个准确解实际上是比较困难的，在科学和工程领域中许多逆问题都具有第一类或者第二类积分方程的形式，由于系统条件数较大的原因，直接基于最小二乘法的经典数值算法是无效的。因此，需要应用特定的正则化技术到实际工程应用中。

2 新型分数阶Tikhonov正则化技术

国内外学者虽然研究不同形式正则化技术，处理该类问题，但对于不同的重构对象其正则解各不相同，尚未有统一的理论研究技术。据此，为了提高重构模型解的稳定性，本文在以前的研究工作基础上，提出了一种新的分数阶Tikhonov正则化载荷重构技术来处理此类存在的不足和问题。

2.1 新型分数阶Tikhonov正则化

首先，对式(4)中的矩阵A进行奇异值分解可得

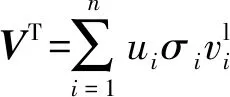
(5)

式中：U=(u1,u2,…,un)和V=(v1,v2,…,vn)分别为由左奇异向量和右奇异向量构成的列正交矩阵。 并且∑为矩阵A的奇异值所构造的对角矩阵，∑=diag(σ1,σ2,…,σn), 且σ1≥σ2≥…≥σn≥0。

新型分数阶Tikhonov正则化载荷重构技术方法为将处理反问题的思想转化为无约束的优化问题，其具体目标函数表达式描述如下

(6)

新型分数阶Tikhonov正则化载荷重构技术对应的分数阶滤波因子表达式为

(7)

其渐进性可被描述如下

从分数阶滤波因子渐进性描述可知，分数阶Tikhonov正则化滤波因子与整数阶Tikhonov正则化相比，收敛性相对慢，即其能够克服正则解的过度光滑性。

2.2 正则参数的选取

L-曲线判别法一种经典的选取正则化参数的有效方法。 对于一系列正则化参数值，用如下表达式进行描述[16]

(lg‖AZ-Yδ‖2,lg‖Yδ‖2)

(8)

式中： ‖AZ-Yδ‖2, ‖Yδ‖2分别为残差范数和正则解范数。通常情况下，最优的正则化参数在L-曲线的拐角处。当选取的正则化参数值比拐角处的值大时，残差范数迅速增加而正则解范数只是很缓慢地减小；当选取的正则化参数值比拐角处的值小时，正则解范数迅速增加而残差范数却很缓慢地减小。因此，选取L-曲线拐角处的正则化参数可以很好地平衡残差范数和正则解范数。在实际应用中，通常只选取曲线拐角处几个点进行计算，即可确定最优的正则化参数值。

2.3 目标函数的求解

式(6)是一类无约束的优化问题，其目标函数的求解有许多优化算法。本文采用超记忆梯度法，其方法描述如下

Zk+1=Zk+dkhk

(9)

式中：hk为搜索方向

(10)

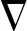
(11)

算法步骤如下

步骤2计算gk， 若‖gk‖≤ε， 则终止。

步骤3根据式(10)计算搜索方向。

步骤4根据式(11)确定步长dk。

步骤5若满足式(9)，则停止；如不满足，则返回步骤1。

2.4 定量评价指标

为了深入定量地评价所提出技术的载荷重构精度，采用均方根误差(Root Mean Square Error，RMSE)公式，其RMSE定义如下所示

(12)

式中：Zactual为实测载荷；Zid为重构载荷。

3 工程应用

镐型截齿截割破碎煤岩试验是在旋转截割煤岩试验振动系统进行的[17]，如图1所示。截割电动机经减速器和转速转矩仪驱动截割臂旋转，采用变频调速方法调节截割臂转速，截割试验台的进给运动通过液压缸实现，经速度传感器反馈，可自动和手动调速。截齿的载荷测试系统由测力装置、压力传感器、信号放大器和Dasp v10智能数据采集和信号处理系统等组成，在旋转截割过程中，截齿所受到的载荷，通过截齿轴向、侧向以及与截齿轴线垂直布置的五个压力传感器的变形量转换为电信号，经多路滑环将信号传入Dasp v10智能数据采集和信号处理系统。

图1 试验振动系统Fig.1 Vibration test system

图2所示的单齿试验载荷是在截齿安装角为40°，煤岩截割阻抗180 kN/m，最大切削厚度20 mm，截割臂转速为41 r/min，牵引速度为0.82 m/min的试验条件下测试得到。

同时也采集到该试验条件下的位移响应信号，如图3所示。然后根据位移响应信号，利用提出的正则化技术来进行载荷识别研究。

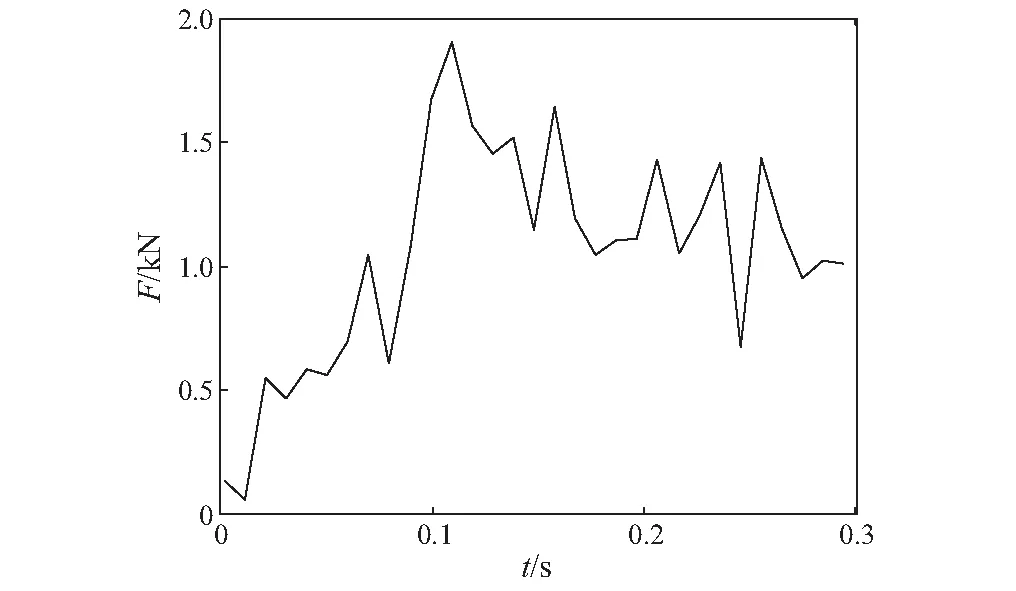
图2 试验振动载荷Fig.2 Test vibration load

图3 位移响应Fig.3 Displacement response

3.1 正则参数λ的影响

所有代码均写在MATLAB 7和运行在HP与2 GB的RAM和Windows 7操作系统。参数设定如下：分数阶次α=0.6， 核函数因子ξ=1。

本文利用提出的一种新型Tikhonov正则化技术来处理在重构过程中出现的病态性、噪声干扰过强、正则解过度平滑等问题。以此确定所提出新技术的工程实践应用性及通用性。然而，关键的问题是如何选择适当的正则化参数以获得最优解。首先，根据L-曲线准则，我们给出了L-曲线的示意图，如图4所示。从图4可以清晰地看出，当正则参数较小时，正则解的范数极其大，而相应的残差解的范数非常小，我们可以推测是由于测量误差导致的。然而，当正则参数较大时，正则解的范数极其小，而相应的残差解的范数非常大。

L-曲线的拐角暗示着过度，它表示的是一种折衷对于残差解和正则解的范数。对分数阶正则化方法中正则化参数的选择不能完全保证适用于所有的不适定性系统。然而，许多例子表明L-曲线准则是一个强大的方法在确定正则化参数方面，适用许多重大的工程和数学问题。

图4 L-曲线准则Fig.4 L-curve criterion

为了进一步探讨正则参数L-曲线对数值例子的影响，从而确定最优的正则参数通过L-曲线。根据L-曲线准则，从图4上选取不同的正则参数值来重构截割煤岩随机载荷，重构结果如图5所示。图5(a)表明载荷重构结果极其不理想归因于较大的正则参数。然而，我们从图5(d)和图5(e)发现，即使正则参数较小(超出一定的范围)，载荷重构结果仍然脱离测量载荷。我们从图5(b)和图5(c)可知，重构结果相对理想。

图5 不同正则参数的重构曲线Fig.5 The reconstruction curve of different regularization parameter

为了进一步地定量评价不同正则参数对重构效果的影响，给出了RMSE值随正则参数的变化，如表1所示。从表1中的RMSE值可以清楚地判断出，看到L-曲线拐角处的正则参数值给出的重构结果, 和其他参数相比，拐角处的重构效果较为理想。最佳的正则参数值在L-曲线拐角处，即在试验范围内，最优正则参数值为λ=10-2。

表1 正则参数对载荷重构的影响

3.2 核函数因子κ的影响

核函数因子ξ的变化直接影响载荷重构的效果，研究理想ξ的值至关重要。参数设置如下：α=0.6，λ=10-2，ξ取整数值，分别给定为1，10，20，30，40，50，60，70，80，100。重构结果如图6所示。从图6可以看出，随着ξ值得不断增大，重构载荷明显偏离实验载荷。为了进一步地定量评价不同核函数因子对重构效果的影响，给出了RMSE值随核函数因子的变化，如表2所示。从表2中的RMSE值可以清楚地判断出，RMSE随核函数因子的增大而增加。因此，建议采取ξ值为1比较理想。

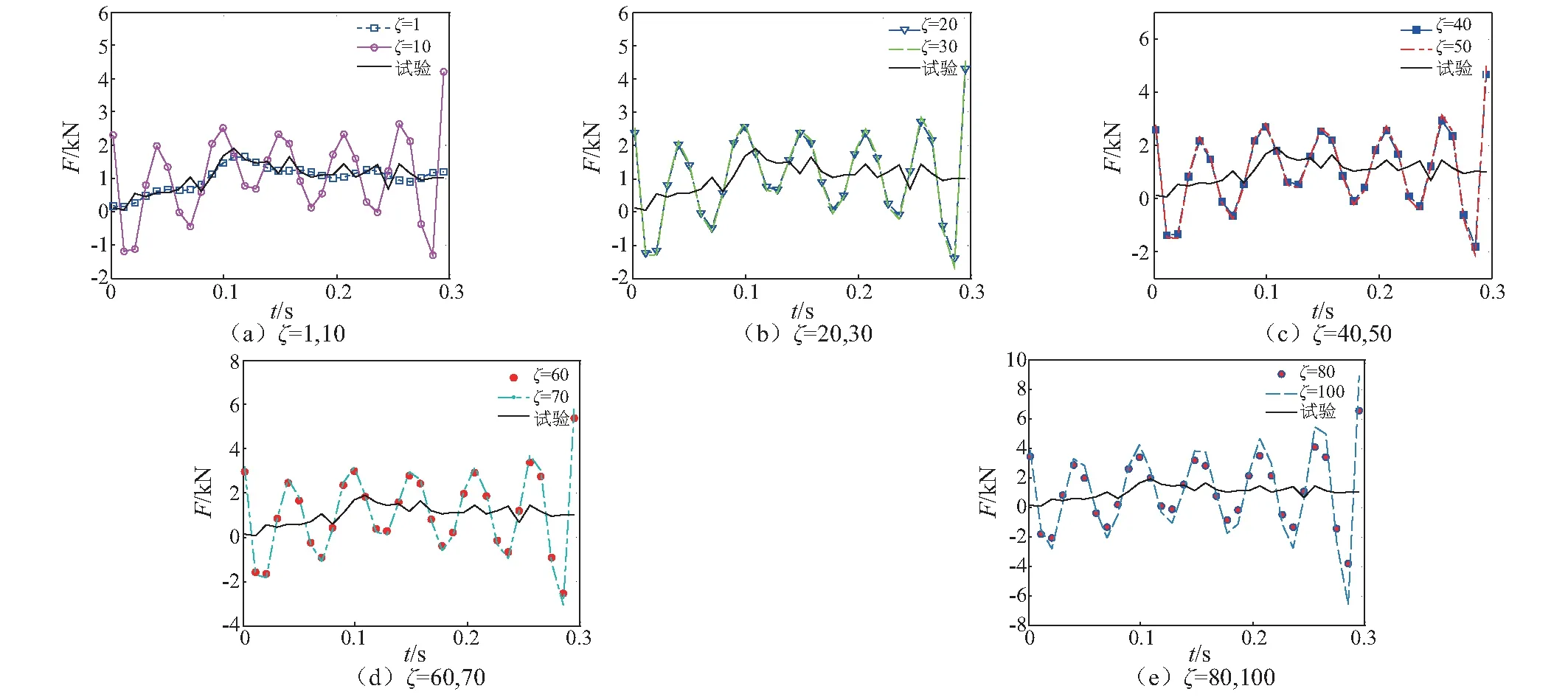
图6 不同核函数因子的重构曲线Fig.6 The reconstruction curve of different kernel function factor

ξ11020304050607080100RMSE0.007 60.273 30.288 60.291 30.298 20.314 20.333 30.356 70.424 10.475 0

3.3 分数阶次α的影响

为了深入讨论分数阶次对载荷重构结果的影响，从而确定最优的阶次值或阶次区间。其参数设定如下：λ=10-2，ξ=1。 而阶次α分别给定为0.1，0.2，0.3，0.4,0.5，0.6,0.7，0.8，0.9，1.0。通过结合分数阶Tikhonov正则化及L-曲线给出其重构结果，如图7所示。从图7可以看出，随着分数阶次的增大，载荷虽然都能够被重构出来，但重构的效果却不尽相同。

为了进一步地定量评价不同分数阶次对重构效果的影响，给出RMSE值随分数阶次的变化，如表3所示。从表3中的RMSE值可以清楚地判断出随着分数阶次的增大，RMSE值呈先减小后增大的趋势，存在着最小的RMSE，即存在最优的分数阶次α=0.6综合上述分析， 当正则参数λ=10-2， 核函数因子ξ=1时， 存在最优分数阶次值α=0.6， 此时载荷重构相对较为理想。

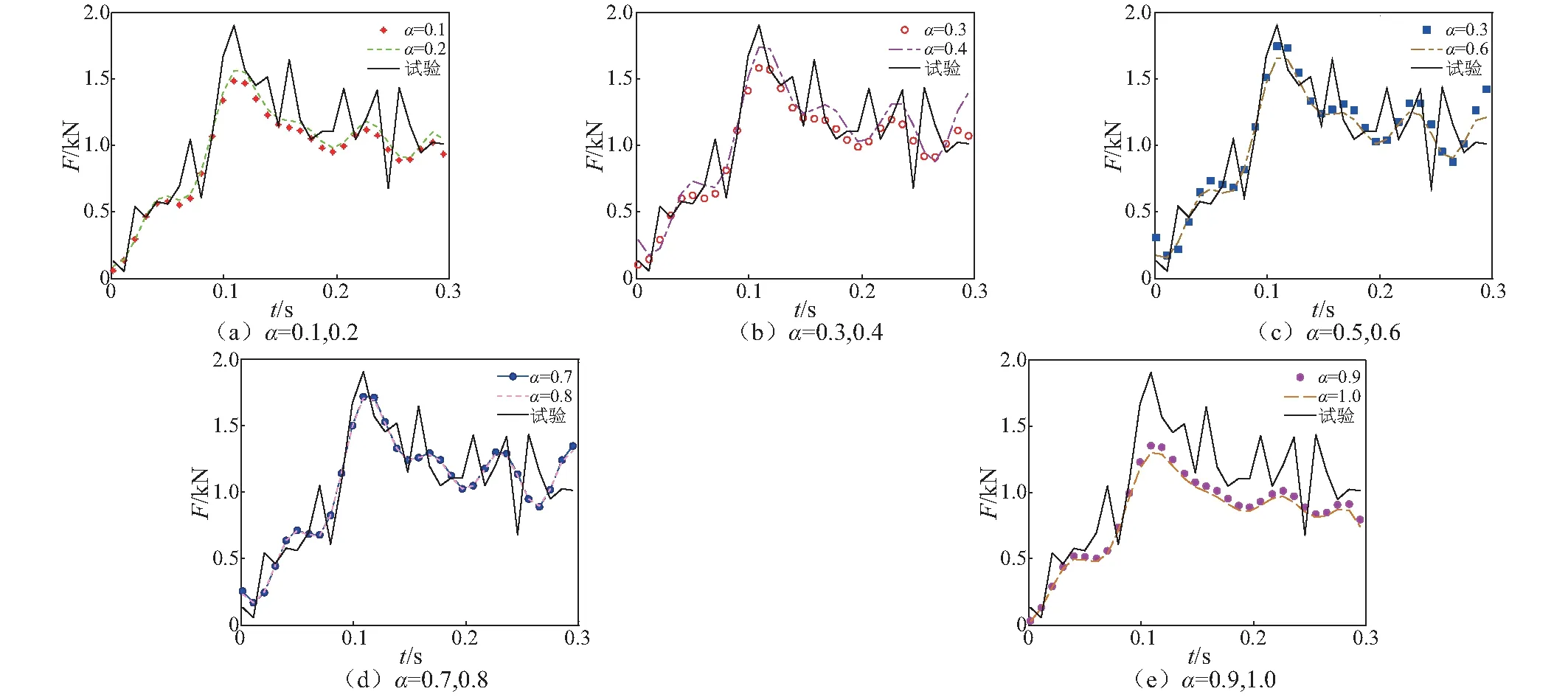
图7 不同分数阶次的重构曲线Fig.7 The reconstruction curve of different fractional order

α0.10.20.30.40.50.60.70.80.91.0RMSE0.739 50.494 90.442 40.216 10.014 00.007 60.056 30.089 81.159 61.343 1

4 结 论

由于载荷重构问题往往存在病态性和对噪声敏感等不足，本文提出了一种新型分数阶Tikhonov正则化载荷重构技术，并把重构结果与整数阶Tikhonov正则化的结果进行比较研究，工程应用算例表明本文提出的方法在动载荷识别方面具有更强的抗噪性和鲁棒性，为解决工程应用中的反问题提供了一种新的有效方法。