舰用中低频伪速度谱测量摆性能研究
赵鹏铎, 曾泽璀,, 张 磊,, 闫 明
(1.海军研究院,北京 100161;2.沈阳工业大学 机械工程学院,沈阳 110870)
现代舰船在海战中必会面临非接触爆炸引起的冲击破坏问题,主要的舰载机电设备和武器电子设备可能因承受过大的冲击载荷而遭受破坏,导致舰船丧失战斗力,处于不利局面[1]。
因此如何准确评估非接触爆炸冲击载荷对舰船设备破坏能力是一个十分重要课题。伪速度谱使用四参数对数坐标表示不同固有频率系统在冲击载荷作用下结构的最大相对位移、最大相对速度和最大加速度曲线变化趋势,能够简单明了地反映冲击载荷的破坏能力,用于确定冲击环境,指导受冲击系统的设计,广泛应用在工程实践中[2-3]。目前获取伪速度谱的途径主要有两种:理论计算方法和传感器测量方法。理论计算方法主要包括:有限元瞬态动力学计算方法和Duhamel积分方法。传感器测量方法主要包括:机械式伪速度谱测量仪、振子式伪速度谱测量仪、电模拟式伪速度谱测量仪和数字分析方法。理论计算方法中,冲击载荷曲线都是针对理想冲击载荷曲线,从而获得的伪速度谱也比较理想;而在传感器测量方法中,由于传感器自身特性产生的测量误差导致冲击信号测量不准,降低了伪速度谱的完整性和准确性。
目前,由于压电加速度计具有体积小测量频域宽等优点,广泛应用于加速度测量领域。测量伪速度谱主要方法是利用压电晶体加速度计测量冲击载荷的时域曲线并进行数据处理获得伪速度谱,但是,当冲击载荷较大时会激起加速度计的谐振峰,使其产生的电荷不能快速释放,从而产生零漂,零漂现象会影响中低频伪速度谱测量的完整性和准确性[4-9]。所以需要利用簧片仪和低频振子两种测量装置对加速度计测量得到的伪速度谱进行补充和相互验证。但是,簧片仪和低频振子都无法单独测量获得完整的中低频伪速度谱曲线,而且簧片仪在测量低频谱时,由于末端质量位移响应比较大,导致簧片仪根部应力过大而发生断裂,所以低频簧片仪能测频率最低为5 Hz[10];低频振子在测量5 Hz一下的低频谱时由于自身固有频率低,具有弹簧的拉伸、压缩量大和质量块重的缺点,固有频率为9.62 Hz的低频振子仅质量块重量就为8.4 kg[11]。
因此,需要研究体积小、重量轻的一种新型中低频伪速度谱测量装置来代替低频振子和簧片仪,独立完成中低频伪速度谱的测量。冲击环境主要包括垂向冲击和横向冲击,在水下非接触爆炸作用下,水面舰船主要承受垂向冲击,潜艇主要承受横向冲击。横向冲击对舰载设备的破坏能力不逊于垂向冲击,并且各国设备抗冲击标准中都涉及到横向冲击谱标准值[12-13]。所以横向冲击伪速度谱的测量同样十分重要。接下来主要针对非接触爆炸所产生的横向冲击环境,利用德国BV043/85标准中的横向冲击位移谱值作为参考,从而进行伪速度谱测量摆的性能研究。
1 测量摆原理及运动方程解析求解
1.1 测量摆原理
由于低频振子重量大不方便携带、中频簧片仪虽然结构紧凑但是存在多阶模态响应叠加影响测量精度,从而设计一种新型的中低频伪速度谱测量装置,即测量摆。测量摆原理如图1所示,其结构与簧片仪相似,为悬臂梁-集中质量块结构,其与簧片仪的区别在于将簧片仪固定端的完全约束固定连接改变为铰链弹性连接,并选用扭簧为弹性元件,其包括以下几个部件:铰链、扭簧、摆杆和质量块。测量摆的工作原理:基础在冲击载荷作用下,其冲击响应主要表现为,质量块和摆杆绕着铰链以一定的频率和振幅振动。

1-连接器;2-位移传感器;3-摆杆;4-质量块;5-凸轮;6-扭簧图1 测量摆原理图Fig.1 Schematic diagram of measuring pendulum
根据转矩平衡定理式(1),可以获得冲击测量摆运动微分方程式(2)
(1)
(2)
式中:kt为弹簧扭转刚度,N·mm/rad;L为摆杆旋转中心到质量块重心的距离,mm;m1为质量块量,kg;m2为摆杆质量,kg;θ为摆杆的摆角,rad。
由于sinθ的存在,式(2)为非线性方程。而且只有在θ<1°(也就是小振幅条件),此时式(2)才能近似于线性方程。但是各国都有对应的冲击环境标准,其中德国BV043/85标准中的横向冲击位移谱值为47 mm。因此测量摆的实际测量角度响应幅值高达30°,测量摆在冲击谱测量过程中存在非线性效应。为研究测量摆在±30°范围内的测量性能是否明显受到非线性效应影响,分别利用解析法求解非线性方程、有限元方法和实验进行研究,从而验证测量摆用于实际伪速度谱测量的可靠性。
1.2 非线性方程解析求解
在这里引入sinθ的泰勒级数展开式来帮助求解方程,如式(3)所示。
(3)
所设计的测量摆在对应实验冲击载荷作用下其摆角不超过30°,其所对应的sinθ泰勒级数展开式前两项与sinθ数值相差百分比在0.01%之内。因此sinθ泰勒级数展开式的前两项就可以作为sinθ的近似解。通过联立式(2)和式(3)可以获得冲击测量摆的运动微分方程为
(4)
根据Ritz-Galerkin方法,通过满足控制非线性微分方程得到问题的近似解。现将非线性微分方程式(4)表达成
(5)
令
则式(5)可以表达成
(6)
假设式(6)的近似解为
(7)
式中:φ1(t),φ2(t),…,φn(t)为假定的时间函数;a1,a2,…,an为待定的权系数,如果把式(7)代入式(6)可得到近似函数方程为
(8)
并且通过求解积分方程式(9)获得非线性微分方程的近似解
(9)
现以式(7)的一阶近似解为例,求解非线性微分式(2)~式(5),具体求解步骤如下:
令
(10)
将式(10)代入式(8)可求得
(11)
根据Ritz-Galerkin方法求解方程解
(12)
求解式(12),得
(13)
因为式中A0不等于零,所以将式(13)转化为
(14)
求解方程得
代入测量摆结构参数和初始条件,求解式(15)就可以获得测量摆的固有频率,其中A0值取决于瞬态动力学分析所获得的最大角度响应。在这里分别计算5 Hz,10 Hz和20 Hz的测量摆,在计算中发现式(15a)的第一项解更接近与真实解,所以这里只列出式(15a)的解,其计算结果如表1所示。
2 有限元模态分析
为了计算冲击测量摆仿真模态频率,使用有限元软件ANSYS的Mechanical/LS-DYNA模块进行计算。创建冲击摆有限元模型,其中使用BEAM188单元创建摆杆模型,材料为45钢;使用COMBIN14单元创建测量摆的扭簧模型;使用MASS21单元创建测量摆的自由端质量块模型。
根据测量摆实物尺寸创建几何模型并划分网格,并设定边界条件进行模态分析,具体计算结果如表1所示,表中fl为Ritz-Galerkin方法计算频率,fy为有限元模态计算频率,fs为实验模态频率。从Ritz-Galerkin方法计算结果可以看出当冲击角度响应较小时(小于30°),使用一阶近似解就可以获得与数值解法相近的方程解。

表1 冲击测量摆模态计算
由于所计算三种频率的前三阶模态振型类似,这里只列出20 Hz测量摆的前三阶振型,如图2所示。
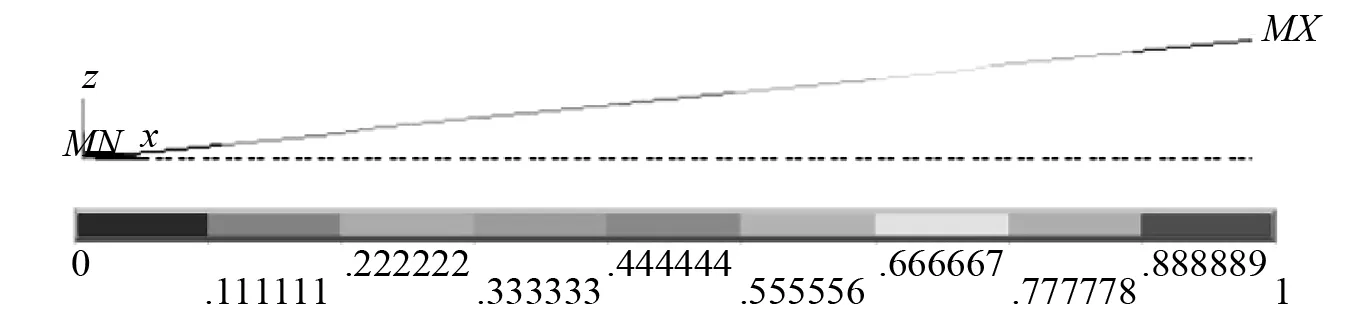
(a)一阶振型
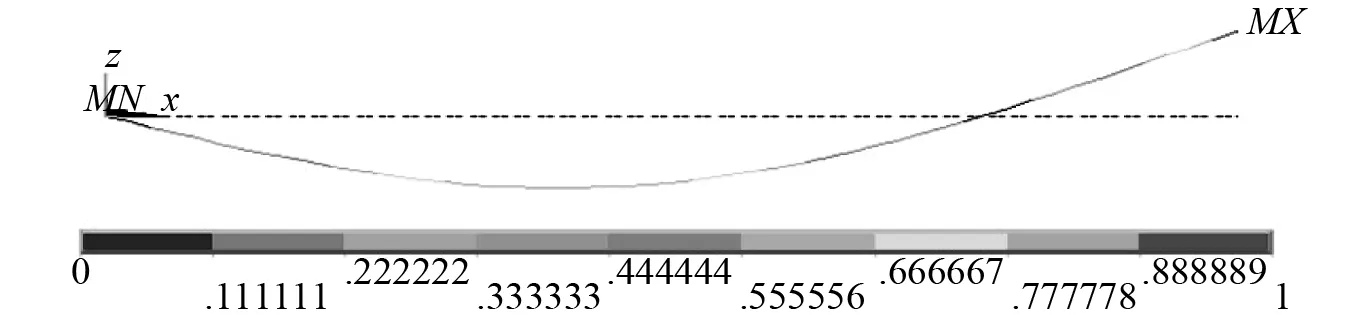
(b)二阶振型
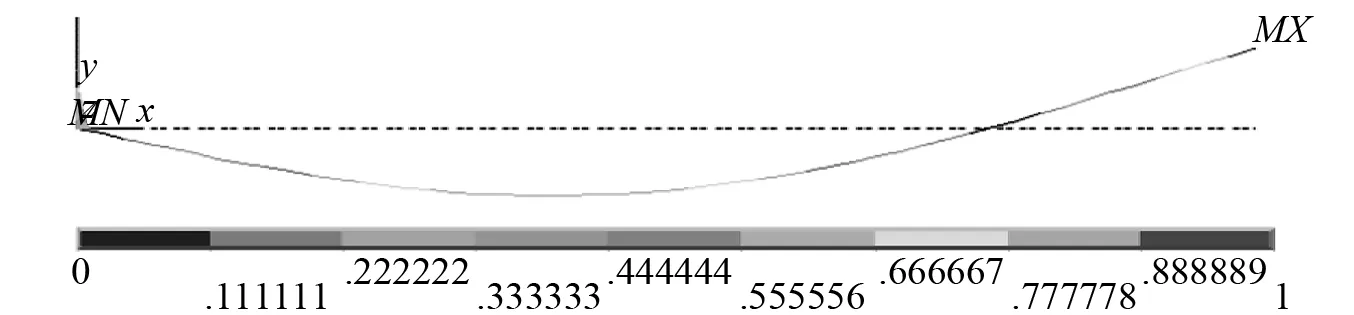
(c)三阶振型图2 测量摆前三阶模态振型图Fig.2 The first three modal shape of measuring pendulum
3 冲击响应计算
在现代海战中舰船经常受到水下非接触爆炸冲击,其主要表现形式为正负双正弦波加速度时域曲线,即正负双波曲线[14-15]。正负双波曲线可以由两个符号相反,时间延迟为脉冲宽度的正弦冲击信号组合而成,正负双波曲线函数为式(16)。
(16)
式中:l(t)为单位阶跃函数。根据实际冲击载荷波形幅值和脉宽换算出一条等效冲击波形用于理论计算所用的理论载荷,如图3所示。
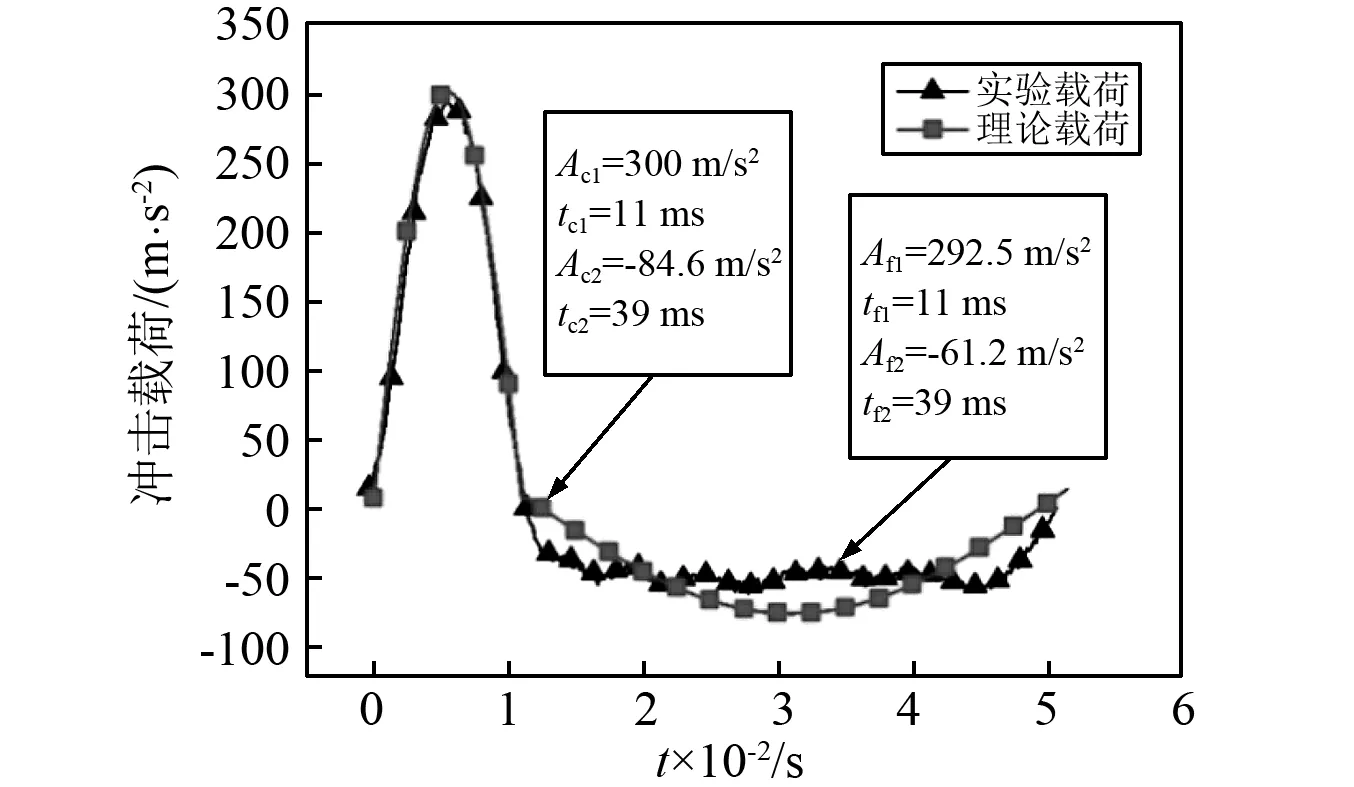
图3 冲击载荷时域曲线Fig.3 Real-time curve of shock loading
利用杜哈美积分方法求解系统在正负双波曲线冲击下的角度响应方程式(17)。
(17)
式中:wd为阻尼固有频率;wn为系统固有频率。将已知的正负双波冲击信号代入式(17)中就能求得系统最大角度响应。
使用MATLAB编写程序计算固有频率为5 Hz,10 Hz和20 Hz冲击测量摆在无阻尼状态下的冲击角度响应,见表2,表中θl为杜哈美积分方法求解角度响应,θy为有限元瞬态响应方法求解角度响应。
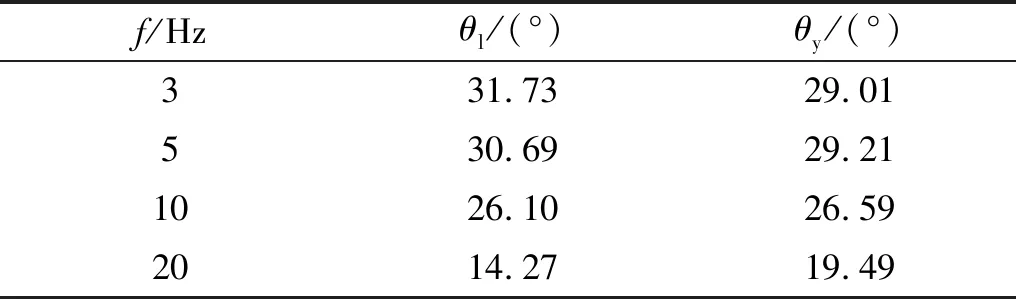
表2 测量摆冲击角度响应
使用ANSYS有限元软件,创建冲击测量摆模型,并计算冲击角度响应。由于实际实验环境较为复杂,对于系统的阻尼系数难以得到精确测量,在本节中所采取计算阻尼系数的方法是通过初步确定系统阻尼比,从而获得阻尼系数,再根据具体阻尼系数计算测量摆的理论冲击响应。根据具体冲击测量摆原理样机的结构参数计算不同固有频率所对应的临界阻尼,如表3所示。
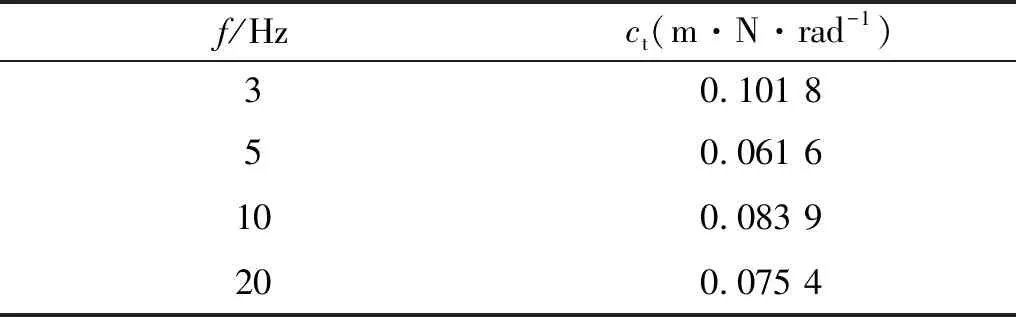
表3 测量摆临界阻尼系数ct
在考虑阻尼比(ζ=0,ζ=0.05和ζ=0.15)的情况下计算冲击测量摆的角度响应,其对应的冲击响应曲线如图4所示,并将最大角度响应转换为水平分量的位移响应见表4。

图4 测量摆角度响应Fig.4 Shock angle response of measuring pendulum
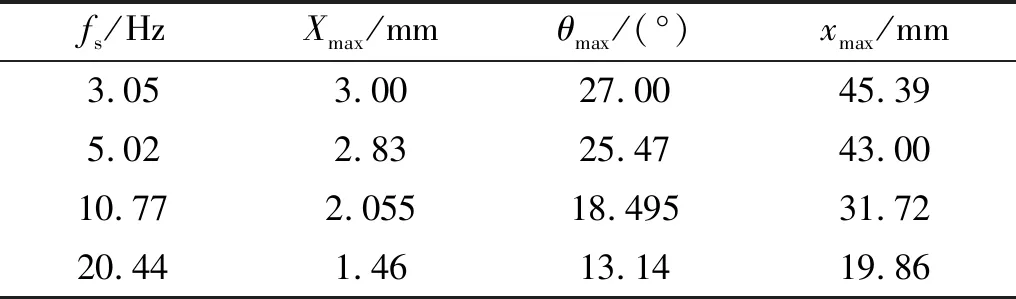
fs/HzXmax/mmθmax/(°)xmax/mm3.053.0027.0045.395.022.8325.4743.0010.772.05518.49531.7220.441.4613.1419.86
根据测量摆摆杆长度为100 mm,通过对摆杆的角度响应进行转换可获得质量块在水平方向位移响应分量,并根据测量摆最大位移响应与伪速度的关系式(18)进行换算绘制中低频段的伪速度谱,如图5所示。
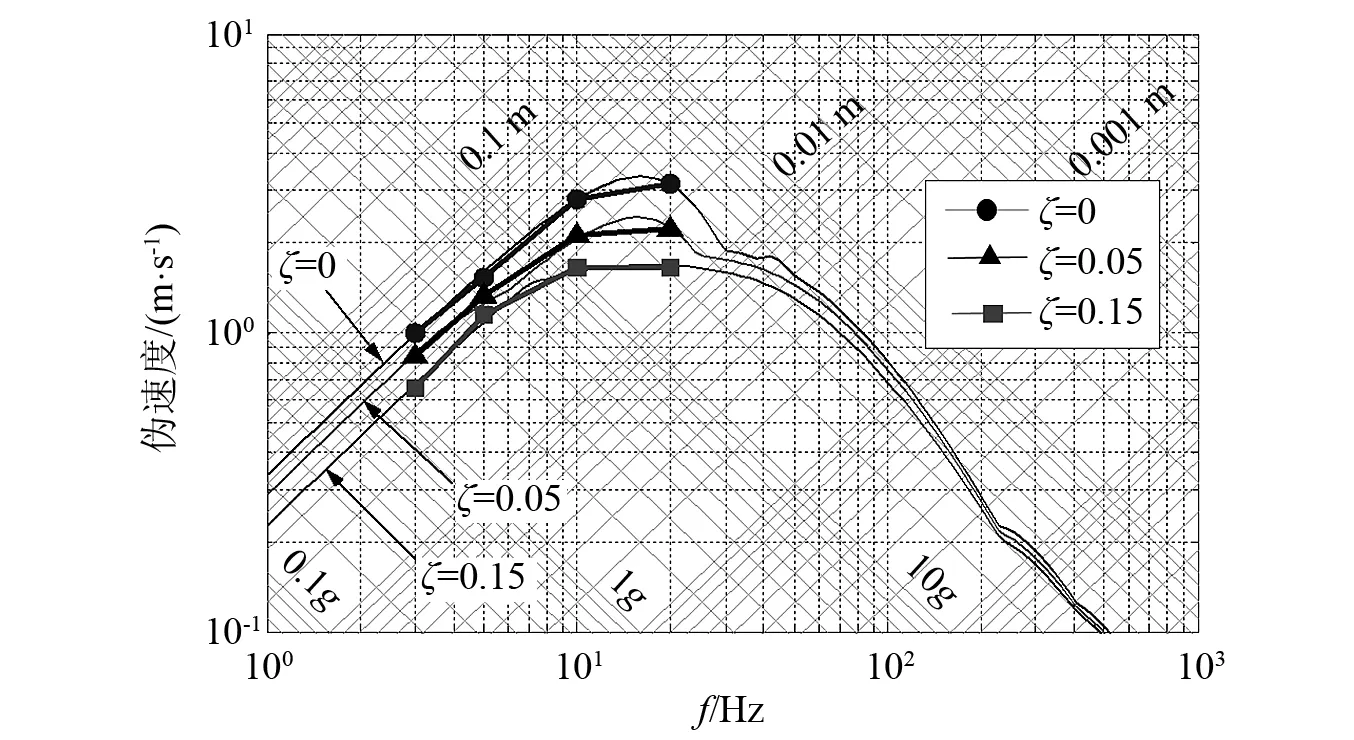
图5 测量摆理论伪速度谱Fig.5 Schematic diagram of measuring pendulum
(18)
4 冲击测量摆原理样机实验
4.1 扫频实验
为了测量冲击测量摆原理样机的实际固有频率,使用振动实验机进行扫频实验。本次实验所使用振动实验台为苏州苏试试验仪器有限公司生产的电动振动实验系统,型号为:DC-3200-36;所使用的实验样品为3 Hz,5 Hz,10 Hz和20 Hz的冲击测量摆;所使用的传感器为INV9822型加速度传感器。加速度传感器一共两个,分别为加速度计1和加速度计2。加速度计1,用于采集质量块的响应信号即冲击响应信号;加速度计2,用于采集实验冲击平台的输入信号即基础输入信号,测量摆实验原理如图6所示。
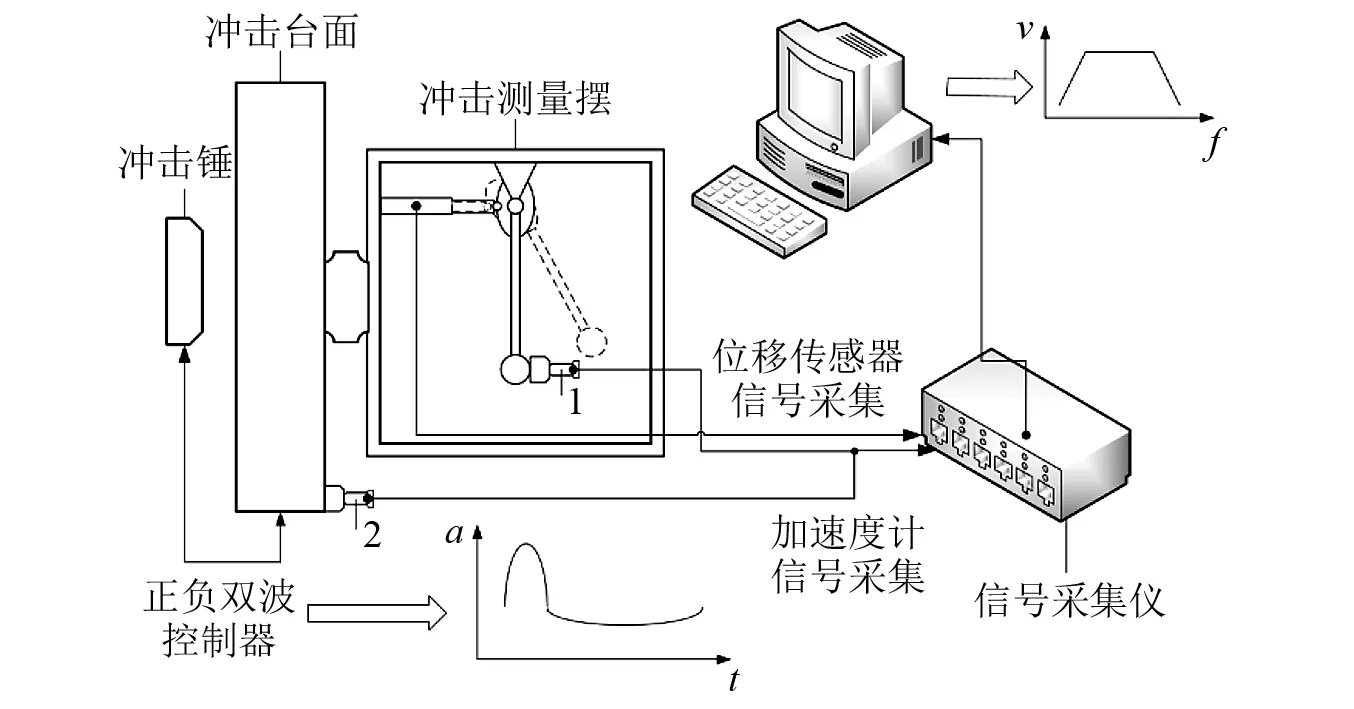
图6 测量摆实验原理图Fig.6 The testing schematic of measuring pendulum
测量摆在实验中的安装方法,如图7所示,其对应模态频率为3 Hz。图8中所示的测量摆为模态频率为10 Hz,其质量块为0.05 kg,摆杆质量为0.033 kg,扭簧刚度为51.2 N·mm/(°),整体装置质量约为4.1 kg,仅为对应固有频率低频振子质量块质量的50%,体积长宽高为150×150×150 (mm),可以看出测量摆明显减小传统测量装置的体积和重量。

图7 冲击测量摆扫频实验(3 Hz) Fig.7 Frequency sweep test of measuring pendulum(3 Hz)

图8 测量摆扫频实验(10 Hz) Fig.8 Frequency sweep test of measuring pendulum(10 Hz)
扫频实验原理,设定振动台的扫频范围,通过观察输出信号与输入信号之间的传递函数,观察曲线的走势,曲线峰值所对应的频率点即为实验原理样机的扫频共振点,通过测量共振点的频率获得实验原理样机的实际固有频率,横向扫频实验果数据如图9所示。
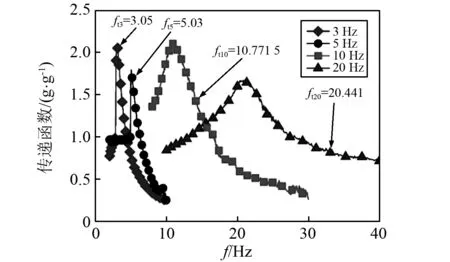
图9 测量摆扫频曲线Fig.9 Schematic diagram of measuring pendulum
从扫频实验结果可以看出,冲击测量摆原理样机固有频率与实际理论设计固有频率之间有一定的差别。
4.2 冲击实验
(1)冲击载荷
为了测试冲击测量摆测量伪速度谱的性能,使用电动振动实验台进行冲击实验,所设定的冲击载荷为正波峰值30g,脉宽为11 ms;负波峰值-8.4g,脉宽为39 ms。实际通过加速度计测量实验台实际运动获得如图10所示的冲击输入载荷波形。
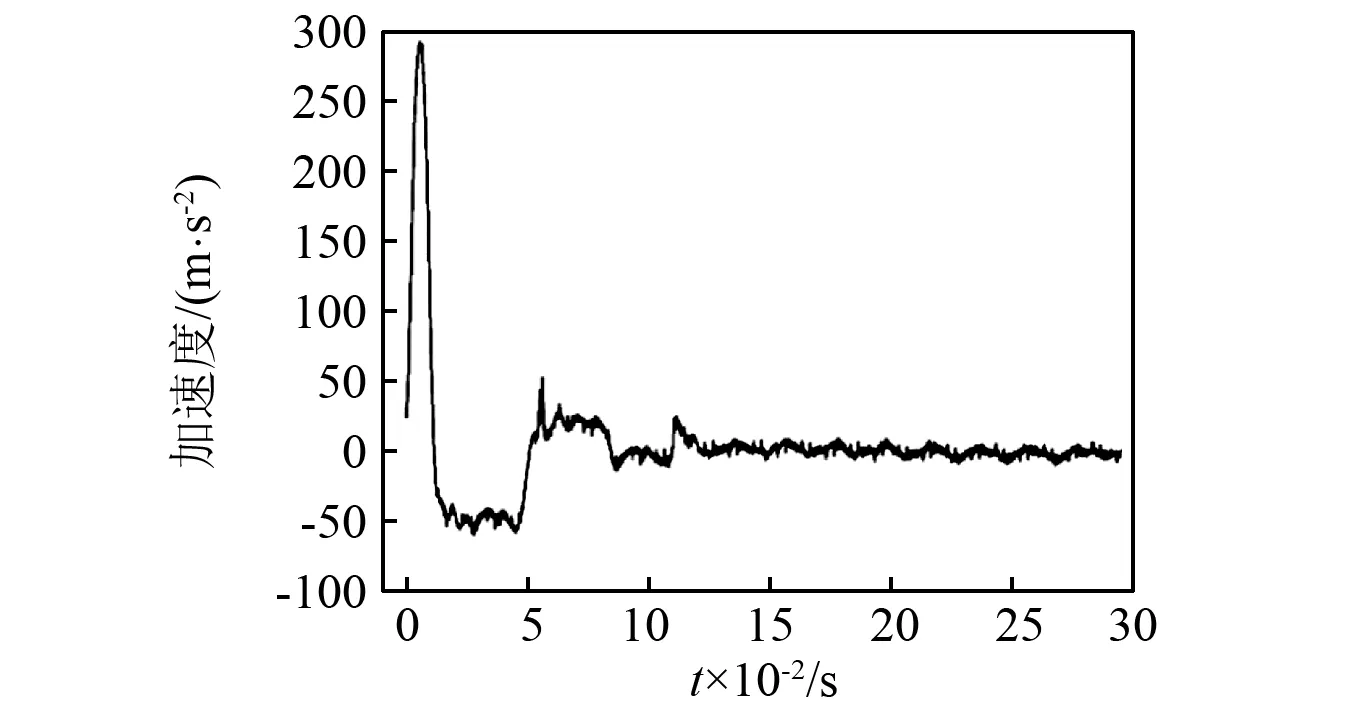
图10 实验冲击载荷Fig.10 Testing shock loading curve
(2)冲击实验原理
为了更好地测量冲击测量摆的冲击响应,使用位移传感器测量冲击响应。测量冲击测量摆的冲击响应原理:使用位移传感器测量凸轮升程间接获得摆杆的摆角,具体工作原理如图6所示。
根据上述的冲击载荷对冲击测量摆原理样机进行冲击实验,通过对冲击加速度输入信号和加速度输出信号进行滤波处理,并且将输入和输出加速度信号进行二次积分处理成时域位移曲线;通过位移传感器输出曲线计算冲击测量摆的角度响应。
4.3 冲击测量摆实验数据分析
根据冲击测量摆的测量原理,在规定的冲击载荷作用下,位移传感器测量响应曲线如图11所示。图中Xnmin为位移传感器的初始位置(mm),不同装置上的位移传感器由于装配差别其对应的初始位置不同;Xnmax为位移传感器的最大响应值(mm)。
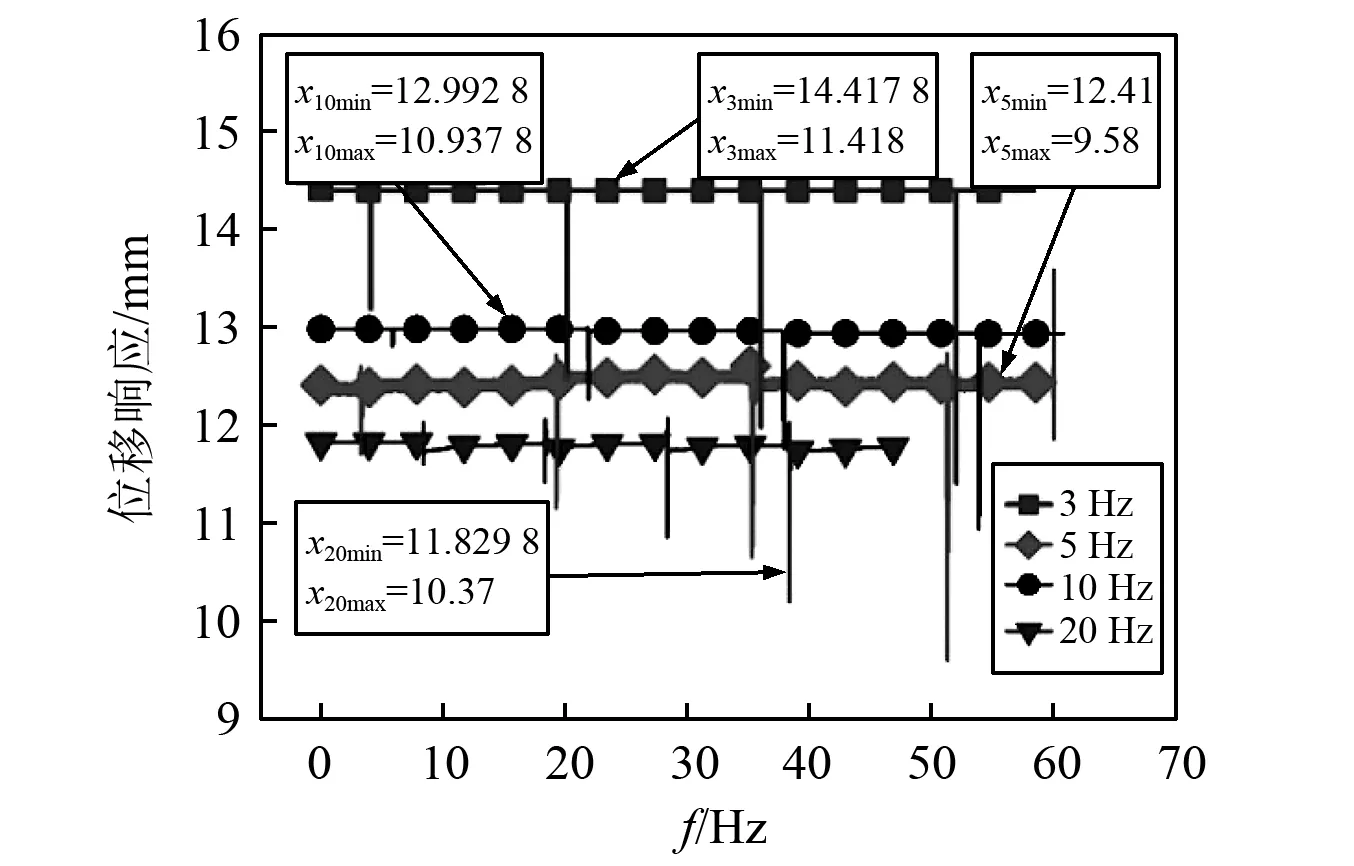
图11 测量摆位移响应Fig.11 Shock displacement response of measuring pendulum
根测量摆凸轮机构与位移传感器测量角度响应的原理,可以将实验中所测量的位移传感器最大位移响应转换为测量摆的冲击角度响应,其具体转换公式如式(19),测量摆水平位移响应如表4所示,表中fs为实验固有频率,Xi为初始位移,Xmax为最大位移,θmax最大角度响应,xmax最大水平位移响应,其中Xmax=Xnmin-Xnmax。
(19)
将测量摆与低频振子所测得冲击响应进行一定转换后绘制成伪速度谱,如图12所示。
5 结 论
通过建立测量摆运动微分方程获得其模型的一阶固有频率,根据任意激励下系统冲击响应所涉及的杜哈美积分方法求解系统在正负双波曲线冲击下的角度响应;同时对测量摆模型使用ANSYS软件进行模态计算和瞬态动力学分析获得其对应的模态频率和角度冲击响应;最后对测量摆原理样机进行扫频和冲击试验,测量其固有频率和角度冲击响应。根据角度冲击响应进行数据处理转换转变成伪速度谱,根据研究内容,主要结论如下:
(1)由于传统加速度计在强冲击作用下产生零漂现象导致中低频段伪速度谱测量数值误差为1~2个数量级,通过理论计算数据和实验数据可以表明测量摆可以较准确测量中低频段伪速度谱,并且通过冲击实验验证了测量摆测量性能,可以准确校验加速度计所测中低频段的伪速度谱。
(2)测量摆相对传统的低频振子,减少了空间尺寸大小和装置整体质量,模态频率为10 Hz时其整体装置质量仅为对应模态频率低频振子质量块质量的50%;与簧片仪相比,测量频域范围广,能够测量5 Hz以下的伪速度谱。

