考虑地震波随机性及水位影响的高土石坝易损性研究

靳聪聪, 迟世春, 聂章博

(1.大连理工大学 建设工程学部，大连 116024；2.大连理工大学 海岸与近海工程国家重点实验室，大连 116024)

进入21世纪以来，我国高度重视能源结构优化和清洁能源发展，因此以高坝大库为代表的国家水电战略开发得到迅猛发展。然而开发建设的高坝大多位于我国地震动活跃的西部地区，加之近年来我国频发强震，如汶川大地震和芦山地震等，造成相当数量大坝的震损破坏，所以高坝抗震安全研究就显得尤为迫切[1]。高土石坝在坝址要求、筑坝材料、抗震设计等方面较其它坝型更有优势，因此得到广泛的应用和迅速发展[2]。

高土石坝地震易损性评价能够描述地震动强度与大坝震害关系的程度，为高坝抗震安全提供参考依据。20世纪70年代，核电站首次采用地震易损性评价，随后基于易损性的抗震性能评估在房建、大坝、桥梁等多个领域不断发展和深入[3-6]。其中增量动力分析(Incremental Dynamic Analysis, IDA)法由Vamvatsikos[7]进行详尽的阐述和总结后，在诸多领域地震易损性评价中[8-9]得到应用。Jalayer[10]提出的多样条分析(Multiple Stripe Analysis，MSA)法无需将地震动强度参数(Intensity Measure, IM)调至使结构反应超越极限状态，即可对离散的IM进行易损性评价。Baker[11]研究发现MSA方法在一定结构分析数量下比IDA方法更有效估计易损性方程参数。

高土石坝由于规模巨大、结构复杂，在进行地震易损性分析需要考虑更多可能影响易损性的因素。地震动输入数量对地震易损性曲线的绘制有一定影响，尤其是位于地震区域活跃地带的高土石坝；高土石坝在建设和运行过程阶段，库水位对大坝数值分析有影响，尤其是遭遇地震时，不同的库水位工况对大坝地震易损性的影响研究。本文主要研究地震动输入数量的确定和库水位对高土石坝地震易损性的影响。首先采用动力固结程序SWANDYNE II[12]对高土石坝在正常蓄水位工况下进行动力分析，对每个地震动强度，分析40条不同地震波作用下的高土石坝震陷率，然后采用MSA法分析高土石坝的易损性曲线和破坏概率。通过不同地震波数量下高土石坝地震易损性参数的分析，确定合适的地震动输入数量；最后根据确定的地震动数量分析汛限水位、设计洪水位、正常蓄水位和校核洪水等库水位和地震动强度作用下的地震易损性曲线，分析不同水位对高土石坝地震易损性的影响。

1 地震易损性评价

易损性能够对结构合理性进行安全评价，并且可以提供结构的安全裕度。将易损性研究引入土石坝的抗震安全评价已成为当今坝工抗震安全研究的热点。其中孔宪京等[13]选取15条地震波，采用IDA方法研究250 m级标准面板堆石坝的地震易损性曲线和破坏概率。王笃波等[14]选取3条地震波，考虑筑坝料参数的随机性，采用基于变形的易损性方法对云鹏心墙堆石坝进行分析。庞锐等[15]选取15条地震波，采用MSA方法分析200 m级规则心墙堆石坝地震易损性曲线。在分析土石坝易损性时，通常分析正常蓄水位下的易损性情况，而没有考虑不同库水位工况下的地震易损性情况。这些研究也没有讨论输入地震波数量对地震易损性曲线的影响，因此需要考虑水位和输入地震动数量对高土石震害易损性的研究。

1.1 MSA方法

易损性曲线是描述结构反应在对应IM下超过破坏状态的概率，其中横坐标常选择地震动峰值加速度(PGA)或谱加速度(Sa)，纵坐标为结构反应超过规定破坏极限状态。一般假设地震易损性符合对数正态分布，易损性方程表示为[16-17]

(1)

式中：Pf(C|IM=X)为地震动强度参数IM=X作用下导致结构达到破坏状态的概率，IM=X为地震动参数(如PGA或Sa);Φ为标准正态分布函数;θ为易损性方程的平均值;β为ln(IM)的标准差。

对于每一个地震动强度Xi，统计出地震波中超过极限状态的地震波数量。假设观察得到每条地震波不超过或者超过结构破坏状态与其他地震波之间是相互独立的[18]，当IM=Xi时，在ni组地震波中有zi组地震波导致结构破坏的概率为

(2)

式中:Pi为在IM=Xi时地震动下结构发生破坏的概率。

似然函数表示为

(3)

式中:∏为连乘符号;m为IM水平数量;ni为超越极限状态的数量;zi为IM=Xi时地震波的数量。

易损性方程参数的θ和β的最大似然估计值如式(4)所示

(4)

上述MSA方法进行易损性分析的主要步骤,如图1所示。

图1 易损性计算流程图Fig .1 Flow chart of the Fragility calculation

1.2 地震波选取

Shome[19]指出10～20条地震波可以确保精确地估计出结构进行地震需求估计。但是由于高土石结构复杂，地形和地质条件较一般建筑物都有较大不同，当其受到地震荷载作用时，大坝的动力响应有着一定的随机性，即采用不同地震动进行大坝动力分析得到的结果不尽相同，因此在进行动力分析时虑地震动输入数量对高土石坝的抗震性能的影响是有必要的。为了分析高土石坝地震易损性和地震动输入数量的关系，选择地震波数量为Shome建议值上限的2倍。地震波作为随机过程，其反应谱也具有一定随机性，而规范标准反应谱则更多体现地震动反应谱均值特性，因此高土石坝的地震动输入选择应充分考虑到地震的随机性。本文研究的位于西南地区的某250 m级的高心墙堆石坝，坝址区地震基本烈度为Ⅶ度，设计地震烈度为Ⅷ度。大坝设计基岩水平向峰值加速度采用100年基准期超越概率为 2 %的加速度 0.283g，并根据该工程场地谱作为目标反应谱。选用的40条地震动记录源于美国太平洋地震研究中心(PEER)数据库。在地震记录选择时，不仅考虑到场地条件及地震的随机性，而且兼顾以下因素：地震等级5.0～7.0，震中距10～60 km，场地为岩性地基。这些地震波的PGA、震级和震中距的分布图，如图2(a)所示，40条地震动加速度反应谱，如图2(b)所示。

(a)震级与震中距分布图

(b)40条地震动加速度反应谱曲线图2 40条地震波的分布图及加速度反应谱曲线Fig.2 The PGA distribution and acceleration spectrum curves of 40 earthquakes

由图2可知，这些地震波涉及不同的震级、距离以及强度，其离散性表明该处坝址地震动的不确定性。

1.3 极限状态指标

土石坝在遭遇地震时会出现不同的破损状态，因此对其震害等级划分是进行震害评估和震后重建的关键因素之一[20]。对于土石坝的地震易损性评估，同样需要定义震害等级以及破坏极限状态。根据国内外土石坝震害现场调查，土石坝震害大致分为有坝体裂缝、沉陷、坝身滑坡等，其中沉陷和坝体滑坡最为普遍。土石坝震害等级划分多以三态准则至五态准则标准为主，其中1976年唐山地震，对土石坝采用严重、较重、轻微和完好的四态准则划分标准；Swaisgood[21]通过调查的69座土石坝的分析，以坝顶相对沉陷率为指标，也按照四态准则进行等级划分；2008年5月12日汶川地震，根据专家组意见对土石坝震害情况按照溃坝险情、高危险情、次高危险情三态准则划分。汶川地震后，中国地震局制定了生命线工程地震破坏等级划分标准[22]，该国标对土石坝震害等级划分是按照五态准则划分，具体如表1所示。

表1 土石坝震害等级划分标准

表1仅从用定性角度给出土石坝震害等级划分，但没有明确的定量说明，因此需要选择合适的评价指标来定量评价土石坝的震害等级。坝顶震陷是土石坝震害调查的主要事项，并能直接反应大坝的地震永久变形程度，可作为定量评价的指标[23]。李红军等[24]对国内外高土石坝计算永久变形方法介绍，并指出永久变形在高土石坝抗震性能安全评价中重要作用。考虑到坝顶相对震陷率能够较为合理的分析高土石坝的整体震害状况，是衡量土石坝抗震安全性能的极限状态标准之一[25]。因此，采用能定量分析震害情况的坝顶相对震陷率结合国标中表1对土石坝震害定性描述对土石坝震害等级进行划分。如表1所示，震害等级的Ⅰ级和Ⅱ级中对沉降定性描述为无沉降，因此根据震害等级Ⅲ级至Ⅴ级中沉降定性描述，采用坝顶相对震陷率对土石坝震害等级进行界定，划分为LS1,LS2和LS3三个等级，并建议依次对应国标的震害等级Ⅲ级、Ⅳ级和Ⅴ级。

刘君等通过搜集和整理的123 个土石坝震害实例以及48个土石坝的地震永久变形数值计算结果分析采用现代碾压施工技术修建的土石坝可以抵抗中等乃至较强地震的作用，坝顶地震沉降量不会超过坝高的1%。赵剑明等[26]对坝高为295 m的两河口高心墙堆石坝进行极限抗震分析，在设计地震(0.29g)下的的坝顶相对震陷率为0.39%，当采用极限抗震能力的0.45～0.5g时，对应的坝顶相对震陷率达到0.65～0.72%，并指出最大震陷超过坝高0.7%～0.8%时产生明显震害。王笃波等[27]对100 m高的云鹏心墙堆石坝分析，并将坝顶相对沉陷的0.1%，0.4%，1%作为大坝轻微破坏、中等破坏和严重破坏的临界状态。庞锐等从地震永久变形角度，对200 m级高心墙堆石坝建立坝顶相对震陷率0.5 %，0.8 %和1.2 %作为轻度破坏、中度破坏和重度破坏的界限状态。综合上述分析，并考虑我国近年来新建的高心墙堆石坝采用的现代碾压施工技术，建议对本次研究的250 m级的高心墙堆石坝采用坝顶相对震陷率1.0 %作为LS3对应的定量标准，以取均值的方式确定LS1和LS2对应的坝顶相对震陷率0.3%和0.6%。考虑到震害等级Ⅳ级描述即产生明显震害，因此对LS2坝顶相对震陷率调整为0.7%。

2 典型高土石坝MSA分析

2.1 有限元模型

某高心墙堆石坝的最大坝高为 261.5 m，总库容为237.03×108m3，正常蓄水位为812 m，上游和下游坡度比分别为1.9∶1 和 1.8∶1，如图3(a)所示。最大断面网格有限元模型共有节点1 240个，单元1 197个，如图3(b)所示。

(a)坝料分区

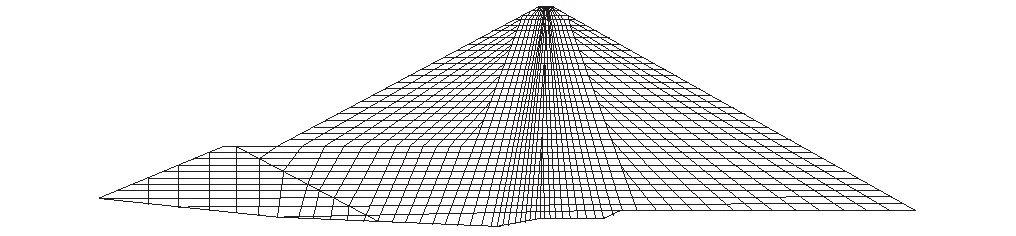
(b)有限元网格图3 大坝坝料分区和有限元模型Fig.3 Dam material zone and finite element model

2.2 弹塑性模型-非线性分析方法

弹塑性模型-非线性分析方法进行高土石坝有限

元计算是高土石坝研究领域的难点和热点。该法采用反映土体真实动应力-动应变关系的弹塑性本构模型，并能够考虑土骨架和流体的流固耦合，因此可全面考虑库水位影响的高土石坝动力研究。其中董威信[28]采用开发的流固耦合弹塑性有限元程序对糯扎渡高心墙堆石坝进行动力响应分析；孔宪京等[29]采用考虑压力相关性的广义塑性模型对面板堆石坝进行地震动力响应分析。本文采用基于PZC弹塑性模型和Biot动力固结理论的动力有限元程序SWANDYNEII对某高心墙堆石坝进行非线性有限元数值计算。

对于频率相对较低的地震情况，可忽略流体相对加速度，采用简化的u-p格式的动力固结方程，如式(5)和式(6)所示。

(5)

(6)

式中:σij为总应力;ρ为两相体密度;ui为土体位移;bi为单位质量上的力;εii为体应变;kij为渗透系数;p为孔隙压力;ρf为液相密度;Q为混合物压缩模型。

对控制方程空间离散后，得到矩阵形式动力固结方程，如式(7)所示

(7)

式中:[M]为质量矩阵;[K]为刚度矩阵;[Q]为耦合矩阵;[H]为渗透矩阵;[S]为压缩矩阵;Fu和Fp分别为固相的荷载和液相的荷载的右端项。

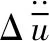
(8)

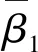
2.3 本构模型和计算结果

对大坝上下游堆石料和心墙料选用PZC弹塑性本构模型，结合室内三轴试验，可确定筑坝料的PZC模型参数，如表2所示。

表2 高土石坝筑坝料参数

进行高土石坝动力计算时，地震动通过黏弹性边界结合等效荷载的形式在有限元模型边界处输入，地震波考虑同时从顺河水平向与竖向双向输入，竖直向地震加速度峰值取为水平向地震加速度的2/3，计算时时间步长取为 0.02 s ，如图4所示。

图4 输入地震波Fig.4 Input earthquake wave

通过SWANDYNEII程序对该土石坝有限元模型进行动力分析得到大坝的竖向永久变形等值线图，如图5所示。

图5 竖向永久变形Fig. 5 Vertical deformation displacement

在地震作用下和上游水压力作用下，坝体竖向永久变形的最大值为0.93 m，发生在坝顶，符合高土石坝一般规律。

2.4 地震易损性分析

本文选取地震峰值加速度PGA为地震强度参数，进行逐级调幅，调幅步长为0.05g，经有限元计算PGA=0.7g时震后变形基本超过坝顶相对震陷率1.0%，因此调幅范围为0.1～0.7g。根据选取地震波，然后进行动力分析，可得到该高土石坝的坝顶相对震陷率。当地震动输入为0.3g时的5条地震波动力分析得到的坝顶相对震陷率的时程曲线如图6(a)所示，同理可得到40条地震动不同PGA对应的相对震陷率，然后采用MSA方法进行地震易损性分析，可以得到地震波峰值加速度PGA与坝顶相对沉陷率关系，如图6(b)所示。

将图6中的数据代入MSA易损性式(2)和式(4)，即可求得对应的易损性参数θ和β值，计算结果如表3所示。

表3 地震易损性参数

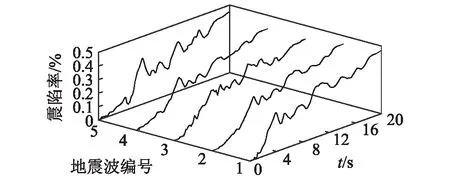
(a)坝顶相对震陷率时程曲线

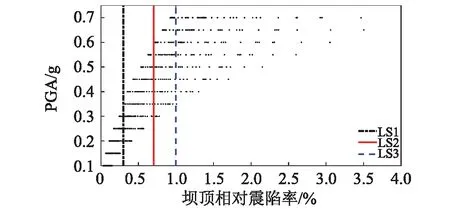
(b)坝顶相对震陷率与PGA关系图图6 坝顶相对震陷率时程曲线以及与PGA关系图Fig.6 Time history of relative seismic subsidence rate and relation of PGA

通过图6中数据和表2代入结合MSA式(1)，得到高土石坝在正常蓄水位工况下的地震动强度和易损性的曲线，如图7所示。

图7 地震易损性曲线Fig.7 Earthquake fragility curve

不同地震动强度情况下的高土石坝三种等级的易损性曲线如图7所示。其中，LS1等级在地震动峰值加速度为0.238g时，发生破坏的概率为50%，同样地震动时LS2和LS3对应的破坏概率为25.8%和1.8%。随着地震动的不断增加，当地震动峰值加速度为0.47g时，LS1发生破坏的概率为100 %，同样地震动时LS2和LS3对应的破坏概率为63.2%和27.8%。当地震动峰值加速度为0.7g时，LS2和LS3对应的破坏概率为96.3%和81.7%。

3 地震波数量对易损性参数的影响

3.1 对易损性参数的影响

不同的地震动输入数量对正常蓄水位工况时的高土石坝易损性影响研究，可通过对易损性方程参数θ和β的变化来进行分析。首先从选取的40条地震波中每次随机抽取5个地震波，通过计算可以得到的5组易损性在LS1,LS2和LS3状态下的地震易损性参数θ和β值，然后按照这种方式，随机不重复抽取100次，然后根据这100组数据，每一组地震波都可以通过式(2)和式(4)估计得出对应的θ和β。这样就可以得出100个θ和100个β，进而得出该地震波数量下θ和β的平均值,不同地震波数量下θ和β的平均值如图8所示。

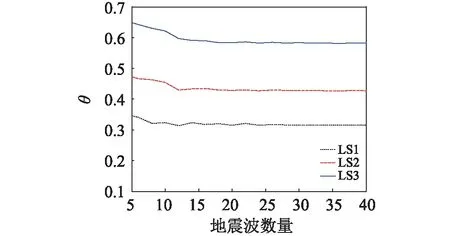
(a) θ变化范围

(b) β变化范围图8 正常蓄水位下不同地震波数量的θ和β值Fig.8 The θ and β of the different seismic waves on the normal water level

如图8(a)表明，在正常蓄水位工况下，高土石坝地震易损性参数θ值随着地震波数量增加而逐渐降低。当地震波数量小于10时，地震波数量对易损性参数θ影响较大；当地震波数量超过23条时，θ值保持恒定不变。图8(b)表明，随着地震波数量的增加，易损性参数β先增大而后趋于稳定；地震动输入数量少于15条时，β值增长较大；当地震波数量超过25时，估计的β值保持不变。从以上对比分析可知，当地震波数量超过25时，地震易损性参数不再波动变化，此时对应的易损性曲线不受地震动数量的影响。通过得到高土石坝地震易损性参数仅通过分析其在平均值情况下随地震波数量变化还不足充分说明易损性参数的变化情况，因此根据计算的易损性参数值的95%置信区间进行估计地震波数量。

3.2 对易损性参数95%置信区间范围的影响

通过计算每组地震波对应的地震易损性参数的θ和β值，对其求得参数的95%置信区间。根据易损性方程的定义可知，ln(θ)和β分别属于t和χ分布，其95%置信区间[30]的上下限可以通过式(9)和式(10)得出

(9)

(10)

因此可以得到每一个地震波数量对应的95%置信区间的100个上限值和100下限值。通过分析地震波数量和易损性参数的置信区间的上下图限值，如图9所示。通过易损性参数95%置信区间的上下限随着地震波数量变化曲线可知，随着地震波数量的增加，95%置信区间的范围逐渐减小并趋于稳定。

图9 不同地震易损性参数95%置信区间的区间值Fig.9 Interval values of 95% confidence intervals for different seismic fragility parameters

由图9可知，易损性参数θ值的上下限范围随着地震动数量的增加，逐渐趋于稳定，当地震波数量达到22条时，θ值上下限范围不再变化；β值数量随着地震动输入数量的增加，亦逐步趋于稳定，在β值达到25条时，该值不再受地震波数量变化的影响。因此，根据对地震波数量的分析以及考虑计算量的因素，对高土石坝的地震动输入参数建议采用25条。

4 不同库水位下的易损性对比

水位升高对高土石坝的安全性产生一定的不利条件，但对该问题仅仅是从定性角度进行分析的，本文通过考虑库水位情况下的高土石坝在地震作用下的易损性，可以从定量的角度对该问题进行研究。因此，采用常见的四种特征库水位：汛限水位(804 m)，设计洪水位(810.92 m)，正常蓄水位(812 m)，校核洪水位(817.99 m)在不同地震动强度下的地震易损性进行分析。通过分析得到的地震动输入数量，再对不同水位工况下的高土石坝进行动力计算，然后采用MSA法分析不同水位和地震强度作用下的地震易损性曲线，不同水位、PGA和易损性的二维和三维关系，如图10～图12所示。

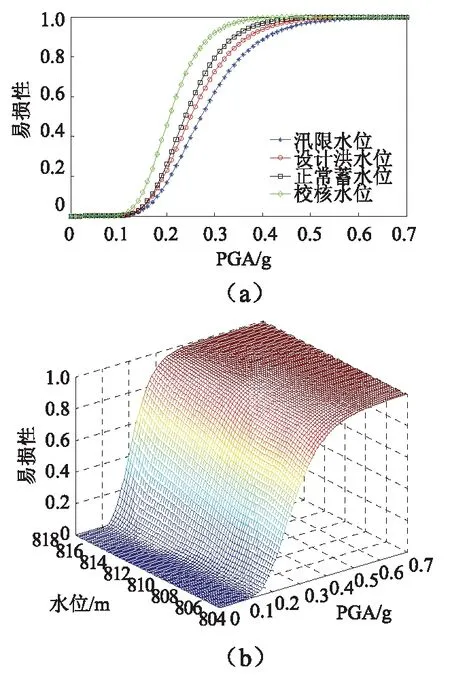
图10 LS1状态下不同地震动强度 和水位作用下地震易损性曲线Fig.10 Seismic fragility of curves earthquake intensity and water level under different LS1

图11 LS2状态下不同地震动强度 和水位作用下地震易损性曲线Fig.11 Seismic fragility of curves earthquake intensity and water level under different LS2

图12 LS3状态下不同地震动强度 和水位作用下地震易损性曲线Fig. 12 Seismic fragility of curves earthquake intensity and water level under different LS3

由图10可知，在高土石坝位于LS1状态时，随着水位的增加，地震易损性也相应提高。从三维易损性曲线可以依次得到804～808 m水位对应的破坏概率，通过三维图可方便的分析不同水位和不同地震动强度下的易损性。当地震动强度为0.2g时，正常蓄水位工况下的破坏概率为26.2%，汛限水位的破坏概率仅为16.8%，设计洪水位则为23.1%，校核洪水位工况下的破坏概率最大，45.7%，接近于汛限水位破坏概率的3倍。汛限水位、设计洪水位和校核水位破坏概率达到50%时，对应的地震动强度分别为0.273g,0.251g和0.206g。

由图11可知，LS2状态下的不同水位对应的破坏概率通过二维和三维易损性曲线得到。当地震动强度为0.4g，四种特征水位依次对应的破坏概率为：29.2%,37.1%,44.3%和59.6%。汛限水位、设计洪水位和校核水位破坏概率达到50%时，对应的地震动强度分别为0.465g,0.438g和0.374g。

由图12可知，四种库水位在地震动强度达到0.7g，发生破坏概率均大于60%，其中校核水位工况下破坏概率达到89.2%。汛限水位、设计洪水位和校核水位破坏概率达到50%时，对应地震动强度分别为0.598g,0.562g和0.497g。

当水位低于正常蓄水位时，高土石坝遭遇地震不同等级的破坏概率有所降低。在校核洪水位状态下，大坝破坏概率较正常蓄水位工况时的3个破坏等级破坏概率有明显的增加。通过对四种特征库水位在高土石不同破坏等级的二维和三维图分析可知，随着水位的不断增加，高土石坝破坏概率也相应增大，因此考虑库水位对地震易损性的影响是十分有必要的。

5 结 论

(1)将高土石坝震害分为3个等级，选取坝顶相对震陷率作为高土石坝震害的评估指标，根据场地谱选取PEER中的40条地震波，并通过SWANDYNE Ⅱ程序对正常蓄水位工况下的高土石坝进行动力分析，采用MSA法对计算结果进行研究并绘制高土石坝地震易损性曲线。

(2)通过对不同地震波数量易损性参数θ和β值分析，当地震动输入数量小于10条时，对应的易损性参数波动较大，随着地震波数量的增加，参数θ值较β值先趋于稳定，当地震波数量大于25条时，两个易损性参数都不再发生变化。采用易损性参数95%置信区间对两个参数分析可知，θ和β值分别在23条和25条时，置信区间上下限不再变化。通过易损性参数分析和有限元动力计算量的综合分析，建议对高土石坝地震易损性分析采用的地震动输入数量为25条。

(3)利用确定的地震波数量进行动力分析，采用MSA法对四种特征水位进行易损性分析可知，汛限水位在高土石坝不同等级的破坏概率最低，而校核洪水位对应的破坏概率最高。进一步对804～808 m的不同水位和地震动联合作用下的地震易损性三维曲线研究发现，随着水位的不断上升，破坏概率不断增加；对同一地震动强度下，低水位情况下发生破坏的概率相应较低。