转子-叶片系统非线性振动和动态稳定性分析

李炳强， 马 辉,2， 曾 劲， 郭旭民， 崔 璨

(1. 东北大学 机械工程与自动化学院, 沈阳 110819； 2.东北大学 航空动力装备振动及控制教育部重点实验室，沈阳 110819)

旋转系统包括轴、叶片和轴承组件等，应用于许多工程机械，如压缩机、汽轮机、航空发动机等。在转子-叶片模型中，轴承通常假定为刚性或带有黏性阻尼的线性弹簧。随着旋转机械结构变得更薄，工作转速更高，可能出现高振幅振动甚至失稳等危险现象，因此对转子-叶片系统的稳定性和分岔进行研究是必要的。

考虑几何非线性以及振动大变形，Khadem等[1]采用多尺度法研究简支轴在主共振条件下的自由和受迫振动。此外，基于Hamilton原理和谐波平衡法，他们还研究了简支旋转轴的模态组合共振[2]。Shahgholi 等[3]考虑到轴的大变形和拉伸效应所引入的非线性，分析了旋转轴在转速波动影响下，主共振频率附近的非线性振动和失稳现象。Chiu等[4]研究了轴扭转和叶片弯曲振动对多盘转子系统耦合非线性振动的影响。Wang等[5]建立了柔性转子-叶片系统的时变非线性模型，讨论了转子的非线性振动对叶片响应的影响。Sanches等[6]研究了直升机螺旋桨的基础共振现象，基于Floquet理论确定了该非线性系统分叉点的位置，描述了在不同条件下的失稳区域。Bab等[7]采用多尺度方法研究了柔性转子和柔性/刚性叶片的耦合非线性共振，讨论了圆盘偏心量和阻尼对系统失稳的影响。

碰摩力可以使转子-叶片系统发生失稳。Parent等[8]研究了涡扇发动机风扇叶片-机匣的碰摩响应，预测了系统的失稳区域，讨论了系统在失稳频率区间的响应。高喆等[9]研究了碰摩转子在随机扰动下呈现出的非线性动力学特性。陶海亮等[10]建立了转子-轴承系统的碰摩故障模型，分析了碰摩刚度以及静子质量对转子动力学响应的影响。刘昕等[11]采用Hertz接触模型构建了叶片-机匣碰摩力模型，并运用该模型研究了转子-轴承碰摩的非线性动力学响应。碰摩力存在多种形式，对于点碰摩或局部碰摩，碰摩力被认为是周期性脉冲力。Petrov[12-13]应用多谐波的非线性碰摩力研究转子的响应，Sinha[14-15]提出若干碰摩脉冲力的数学表达式，如正弦半波脉冲，矩形脉冲等。Turner等[16-17]采用类半正弦波脉冲力研究叶片-机匣的碰摩。Kou等[18]应用正弦脉冲函数和连续正弦函数模拟叶片-机匣的法向碰摩力。Ma等[19]确定了周期脉冲碰摩力最大值的表达形式。

以上文献中，有些学者将轴简化为简支梁，不考虑轴承支承刚度和阻尼的影响，另外一些学者虽然将轴承考虑为线弹性支承，但是没有考虑支承刚度和陀螺效应对转轴振型的影响。基于此，本文研究了主共振条件下转子-叶片系统受周期性脉冲碰摩力冲击的振动响应和稳定性，分析讨论了轴承支承刚度、阻尼、陀螺效应、碰摩力、摩擦因数和圆盘偏心量等对系统响应幅值以及失稳区域的影响，并通过引入数值积分结果验证本文摄动解的准确性。

1 转子-叶片系统运动微分方程

图1为转子-叶片系统示意图，其中X-Y-Z为惯性坐标系，X为未变形轴的中性轴方向，x-y-z为动态坐标系，附着于轴变形后的截面主轴上，xb-yb-zb为叶片的动态坐标系，xb沿着叶片的宽度方向，yb沿着叶片的厚度方向，zb沿着叶片的长度方向。轴左端的扭簧支承kφ=∞，也就意味着绕X轴的扭角为0，同时固定轴左端X方向的位移，kbz1,kbz2,kby1,kby2分别为轴承1和轴承2沿着Z方向和Y方向的支承刚度，cbz1,cbz2,cby1,cby2分别为轴承1和轴承2沿着Z方向和Y方向的阻尼，为了计算的简化，令kbz1=kbz2=kby1=kby2=k,cbz1=cbz2=cby1=cby2=cbearing。旋转轴的动能和势能可表示为

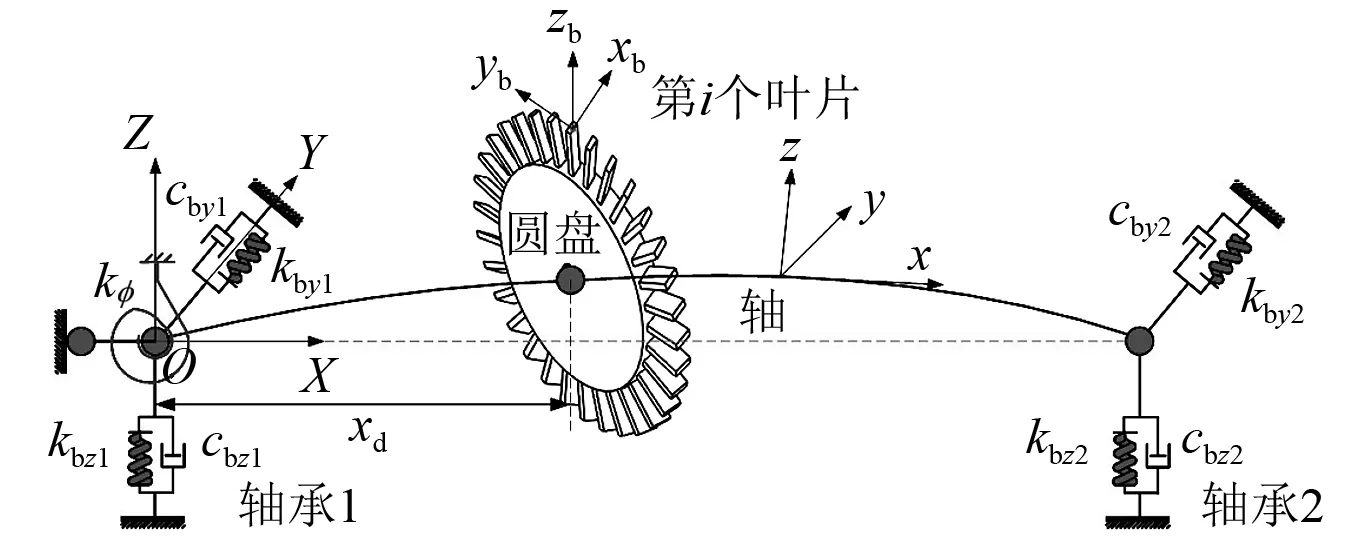
图1 转子-叶片系统示意图Fig.1 Schematic of rotor-blade systems

(1)

(2)

式中：l，m，I1,I2,I3,N11,α,D11,D22,D33分别为轴的长度、单位长度质量、单位长度极转动惯量、单位长度关于y轴的转动惯量、单位长度关于z轴的转动惯量、轴向刚度、轴向应变、扭转刚度、关于y轴的弯曲刚度、关于z轴的弯曲刚度;u,v,w,ω1,ω2和ω3为轴上任意点在惯性坐标系下沿着X,Y,Z三个方向的位移和角速度；“·”为对t求偏导；k1，k2，k3分别为截面的扭转曲率、截面关于y轴的弯曲曲率和截面关于z轴的弯曲曲率。

盘假设为刚性，固定于轴上x=xd的位置，其势能为0，动能可以表示为[20]

(3)

式中:mdisk,Ω,ey,ez,Idisk,Jdisk为盘的质量、旋转角速度、圆盘关于Y方向的偏心距、圆盘关于Z方向的偏心距、直径转动惯量和极转动惯量。

将叶片简化为Euler-Bernoulli梁，对于第i个叶片，扭转位移φi(t)表达为

φi(t)=Ωt+φ(xd,t)+ϑi,i=1, …,Nb

(4)

式中：Nb为叶片数;φ(x,t)为轴的扭转变形;ϑi为第i个叶片的角位置

(5)

叶片的安装角为γ,θ(x,t)和ψ(x,t)分别为轴绕Y轴和Z轴旋转的两个欧拉角，xb,Λi,yb,Rd和ζ分别为任意质点在横截面内沿着叶片宽度方向的位置、叶片的弯曲振动幅值、叶片在横截面内沿着厚度方向的位置、圆盘半径、质点与叶根的距离，考虑到叶片动态坐标系向惯性坐标系的转化，其上任意质点的位置向量为

(6)

则第i个叶片的动能为

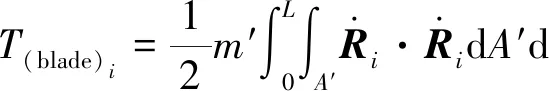
(7)

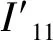
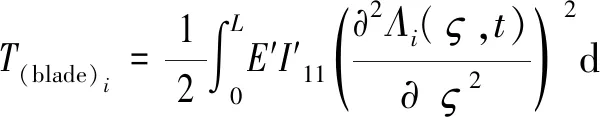
(8)

对所有叶片，总体动能和势能为

(9)

在叶尖处施加周期脉冲碰摩力，其表达式为

(10)

式中：Fn max,tc,tp,t0为最大法向碰摩力，接触时间、周期以及开始碰摩时间。设定μ为摩擦因数，则第i个叶片的碰摩力所做的功为

WFni=μFniΛi(L,t)cosγ-μFni(Rd+L)φi(xd+t)+

Fni(-cosφi+μsinφi)vδ(x-xd)+
Fni(-sinφi-μcosφi)wδ(x-xd)

(11)

Hamilton原理的表达式为

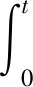
(12)

其中,

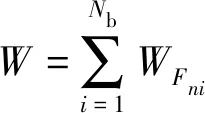
在式(2)中，轴向应变的表达式为

(13)

式中：“′”为对x求偏导。

由图1中支承方式可知，固定左端轴向位移，而右端可以沿着轴向移动，即α=0，可得

(14)

轴上任意点绕Y轴和Z轴旋转的两个欧拉角θ(x,t)和ψ(x,t)可以表达为

(15)

转子-叶片系统的响应峰值和失稳区域均发生在弯曲共振频率范围内，而轴的扭转频率要远高于弯曲频率，因此，相较于弯曲惯性项和刚度项，扭转惯性项的值很小，可以忽略。如果v=O(ε)且w=O(ε), 其中ε是无量纲的小尺度参数，则扭转运动的非线性项数量级为O(ε4), 可得

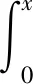
(16)

将式(14)～式(16)代入式(1)～式(6)，可消掉u(x,t),φ(x,t)，θ(x,t)和ψ(x,t)，得到系统关于w(x,t),v(x,t)和Λi(ζ,t)的非线性运动微分方程。采用Coleman变换缩减系统自由度，引入变量ξ和η，表达式为

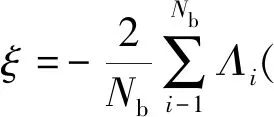
(17)

为了进一步对系统展开降维，采用如下复平面映射

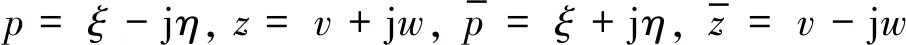
(18)

通过以上变换，方程的数量由2+Nb降为2个，设定轴承，轴和叶片的阻尼系数分别为cbearing,c和cblade。进一步引入如下无量纲变量

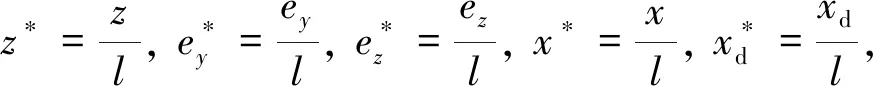
(19)

值得注意的是，在摄动求解中，cbearing,c和cblade数量级为ε2，而Fni,ey和ez的数量级为ε3，其中ε是无量纲的小参数。综合式(1)～式(19)得到转子-叶片系统的无量纲运动微分方程为

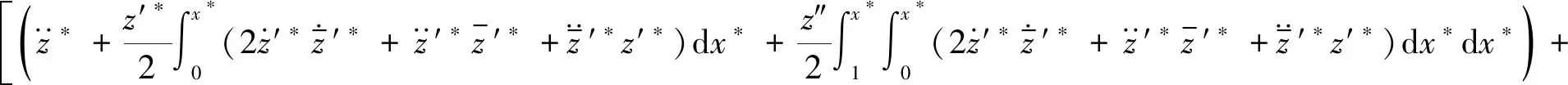
(20)

(21)

式(20)为转子运动微分方程，左侧的项整理后可以分为5类，用5个中括号加以区分，分别代表转子结构参数，圆盘的质量、转动惯量以及偏心距的影响，叶片横向振动的影响，轴承支承刚度及阻尼的影响，碰摩力的影响。式(21)为叶片的运动微分方程，左侧的项整理后可以分为4类，用4个中括号加以区分，分别代表叶片结构参数，转子旋转效应的影响，碰摩力的影响以及转子横向位移的影响。可以看出，轴及叶片的运动是高度耦合的。

式(20)和式(21)都是偏微分方程，直接求解比较困难，可利用Galerkin方法分离变量。为研究主共振频率范围内转子的响应和失稳状态，需要求解其主共振状态下的振型。

叶片可视作悬臂梁，其振型为

ψi(V*)=(sin(βiLV*)-sinh(βiLV*))-

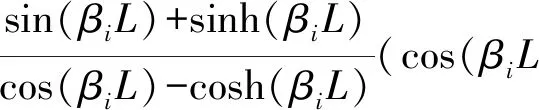
β1L=1.875 1,β2L=4.964 1… 0≤V*≤1

(22)

将轴看做两端弹性支撑的Timoshenko梁，如图2所示，l1,l2为圆盘与两端的距离，截面关于Y轴和Z轴的转角用θy和θz表示，令θ=θy+jθz。盘片系统简化为集中质量点，其质量为mD，转动惯量为Jp，直径转动惯量为Jd，考虑到陀螺效应，轴的振型可以表达为[21]

φni(x)=c1isinαnix+c2icosαnix+
c3isinhβnix+c4icoshβnix

(23)

图2 盘片轴的简化模型Fig.2 Simplified model of shaft-disk-blade

式中：i=1, 2；xi∈[0,li]；c1i，c2i,c3i,c4i为待定常数;αni和βni需要满足

(24)

其中,

(25)

式中：ρ,Is,κ,E分别为轴的密度、截面惯性矩、截面剪切系数和杨氏模量；ω为转子-叶片系统的固有频率，主共振条件下，可认为Ω=ω。定义Θi(xi)为θi的振型函数，则有

(26)

根据两端弹簧支承的边界条件，可得

(27)

在圆盘接界处的边界条件可表达为

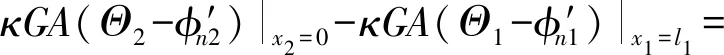
(28)

将式(26)～式(28)代入式(23),即可求得轴在弹支边界下的临界转速及其各阶主共振的振型。轴的各阶整体振型为

(29)

某轴长度为0.595 2 m、截面面积为3.14×10-4m2、截面惯性矩为7.85×10-9m4、杨氏模量为2×1011Pa、密度为7 800 kg/m3,xd=0.407 7 m,mD=0.735 kg,Jp=6.25×10-4kg·m2,不同边界条件下前两阶临界转速，如表1所示，支承刚度k=2×106N/m时的归一化振型，如图3所示，为了验证解析方法的准确性，采用Nastran建模并进行正进动和反进动固有频率对比。从表1中可知，当支承刚度非常大时，弹支轴与简支轴的固有频率比较接近，随着支承刚度降低，固有频率降低，在离心力作用下，两端支承处的相对位移较大。在高阶振动中，盘所在的一侧振幅会相对较小。

用Galerkin方法分离变量，可设定p*(V*,t*)=ψi(V*)P(t*),z*(x*,t*)=φn(x*)Z(t*)，代入式(20)和式(21)，并从0～1积分，可消去变量x*和V*，从而转化为常微分方程，采用龙格库塔方法对若干固定的转速值进行数值求解，从而验证本文多尺度摄动解的准确性。

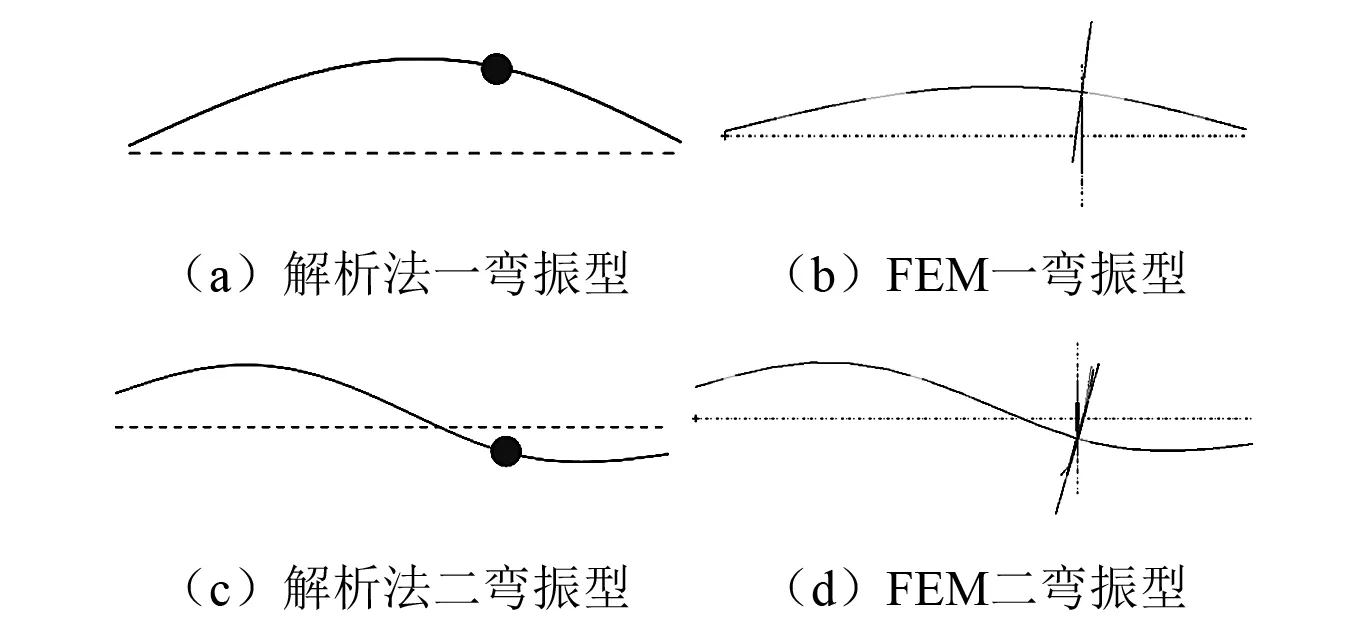
图3 旋转轴的弹支振型 (k=2×106 N/m) Fig. 3 Mode shapes of the rotating shaft (k=2×106 N/m)

边界条件支撑刚度/(N·m-1)一阶临界转速/(Rad·s-1)解析法FEM正进动反进动正进动反进动二阶临界转速/(Rad·s-1)解析法FEM正进动反进动正进动反进动弹支2×106490.29-487.63491.91-488.521 835.10-1 796.221 836.28-1 795.45弹支2×108523.65-518.95523.34-518.482 265.93-2 190.572 261.72-2 189.84简支526.83-521.77526.01-521.432 315.76-2 198.332 312.92-2 194.23

2 多尺度求解

采用多尺度方法进行求解，p*(V*,t) 和z*(x*,t) 可以展开为

p*(V*,t)=εp1(V*,T0,T2)+ε3p3(V*,T0,T2)+…

z*(x*,t)=εz1(x*,T0,T2)+ε3z3(x*,T0,T2)+…

(30)

式中：T0=t,T2=ε2t。为了表征共振频率与正进动频率的接近程度，引入无量纲调谐参数σ=O(1),使Ω*=βf+ε2σ，其中βf为无量纲正进动频率。将式(30)代入式(20)和式(21)，使两端ε和ε3项对应系数相等，通过ε项可确定解的表达形式，代入ε3项可得方程

(31)

(32)

式中：Hz,f(x*,T2),Hz,b(x*,T2) ,Hp,f(V*,T2)和Hp,b(V*,T2) 为久期项，N.S.T为非久期项；βb为无量纲反进动频率；D0=∂/∂T0。设定φf(x*),φb(x*),ψf(V*),ψb(V*)分别为轴和叶片的正进动与反进动振型，根据之前的讨论，可令ψf(V*)=ψb(V*)=ψi(V*),φf(x*)=φb(x*) =φn(x*), 如果方程存在非零解，则必有

(33)

其中，

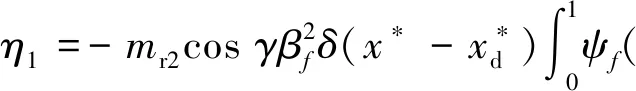
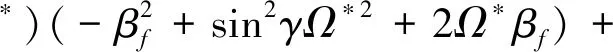
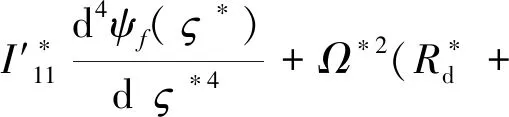
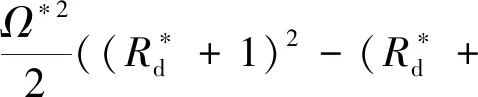
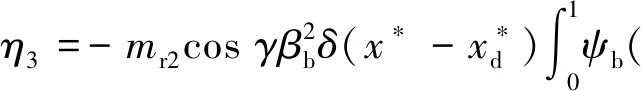
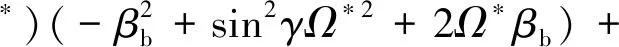
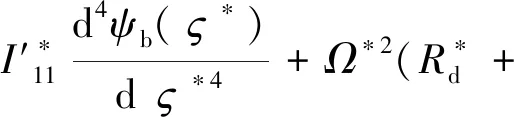
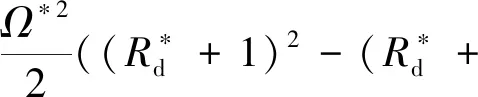
式(33)左侧Jacobian矩阵的特征值可以给出系统的稳定性信息：若所有特征值的实部都为非正值，系统稳定，反之，若存在任意一个实部大于0的特征值，系统不稳定。

对于其他碰摩形式，只要碰摩力在每个旋转周期内对时间可积就可以应用本文的方法。非周期的碰摩力进行如下等效即可

(34)

式中：Fni(t)为作用于第i个叶片上的任意形式的碰摩力。

3 数值算例

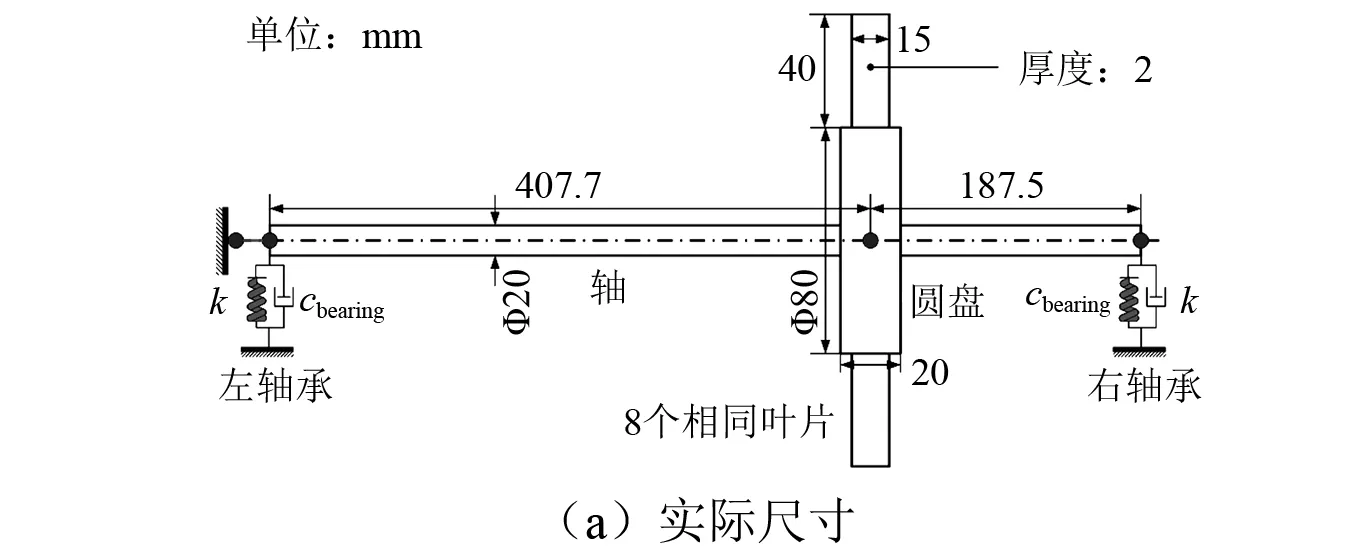
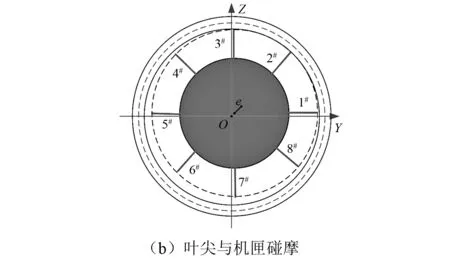
图4 转子-叶片系统示意图Fig.4 Schematic of rotor-blade system

各工况中均采用龙格-库塔数值积分方法验证多尺度摄动解的准确性。图5为不同碰摩力下转子-叶片系统的响应曲线，可以看出系统为硬式非线性，在无碰摩力或碰摩力较小的条件下，系统可以维持稳定。随着碰摩力的增加，非线性增强，共振峰值提高，最大碰摩力的值为0.225时，响应发生分叉，系统存在两个稳定解和一个不稳定的解。

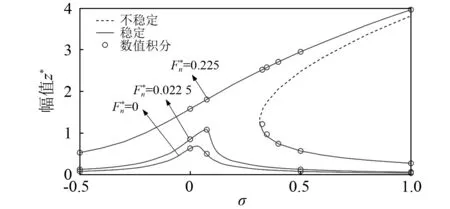
图5 不同法向碰摩力下的响应幅值Fig.5 Response amplitude under different normal rubbing force

图6为不同支承刚度下系统的响应幅值，支承刚度较低时，非线性较弱。当-0.2<σ<0.533时，低支承刚度下，系统的响应幅值较大。但随着支承刚度的增加，系统的跳跃频率升高，不稳定区域和共振峰值也随之增加。

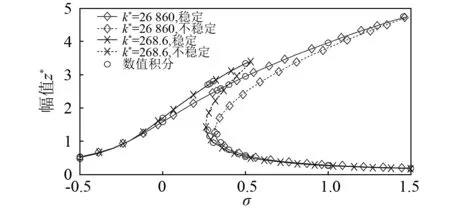
图6 不同支承刚度下的响应幅值Fig.6 Response amplitude under different stiffness

图7为不同摩擦因数下系统的响应幅值，在AB区域，未达到二者跳跃频率，提高摩擦因数，系统的响应只是轻微地增加，几乎保持不变。然而，摩擦因数的增加会提高跳跃频率，通过额外的BC区域，系统的共振峰值得到提高。

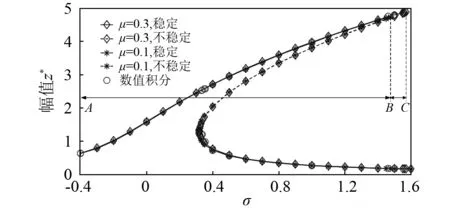
图7 不同摩擦因数下的响应幅值Fig.7 Response amplitude under different friction coefficient

图8为不同圆盘偏心量下的响应幅值，从图中可以看出，圆盘偏心量的增加，与碰摩力增加的情形类似，系统的非线性增强，跳跃频率以及共振峰值也随之增加。

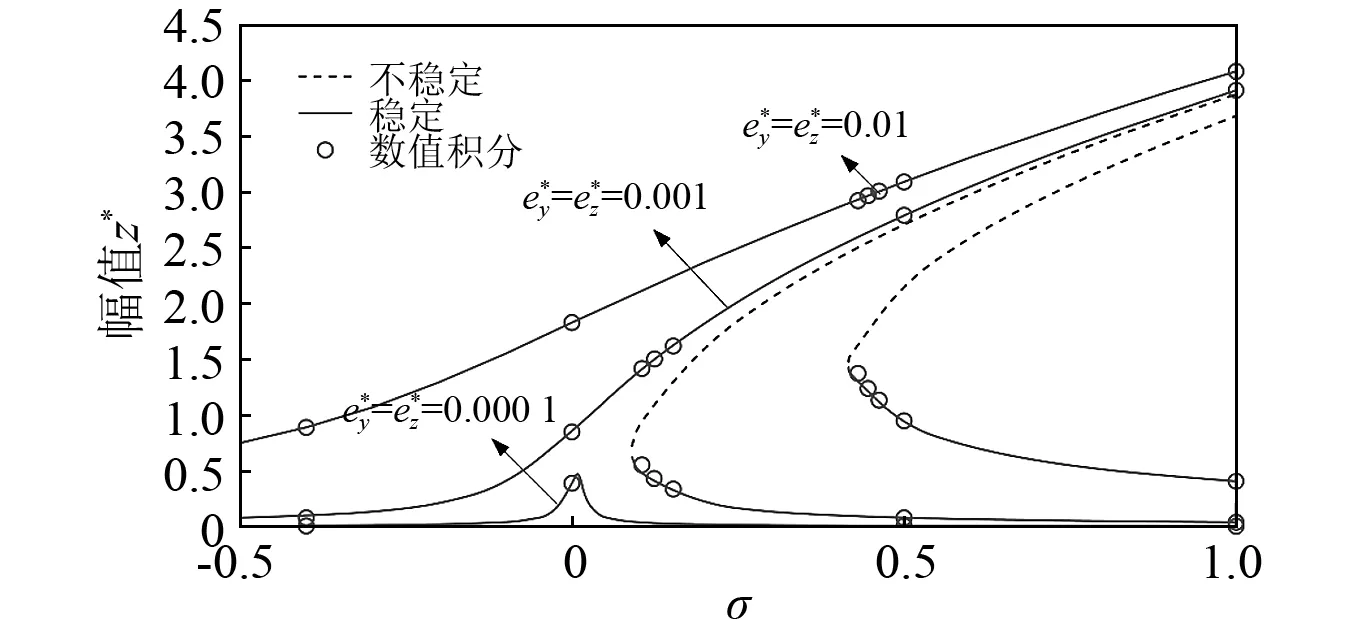
图8 不同圆盘偏心量下的响应幅值Fig.8 Amplitude-frequency responses under different eccentricities

图9为不同支承刚度和转轴阻尼系数下，系统的稳态响应幅值。从图9中可以看出，系统若要达到完全稳定，支承刚度越大，则需要更大的阻尼。相同阻尼下，在未达到跳跃频率时，支承刚度越小，系统响应幅值越大。随着调谐参数的增加，共振分支的响应幅值增加。另外值得注意的是，无论支承刚度的数值大小，过小的阻尼都会使系统发生失稳。

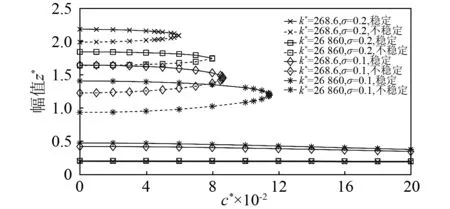
图9 转轴阻尼系数对稳态响应的影响Fig.9 Steady state responses under different damping

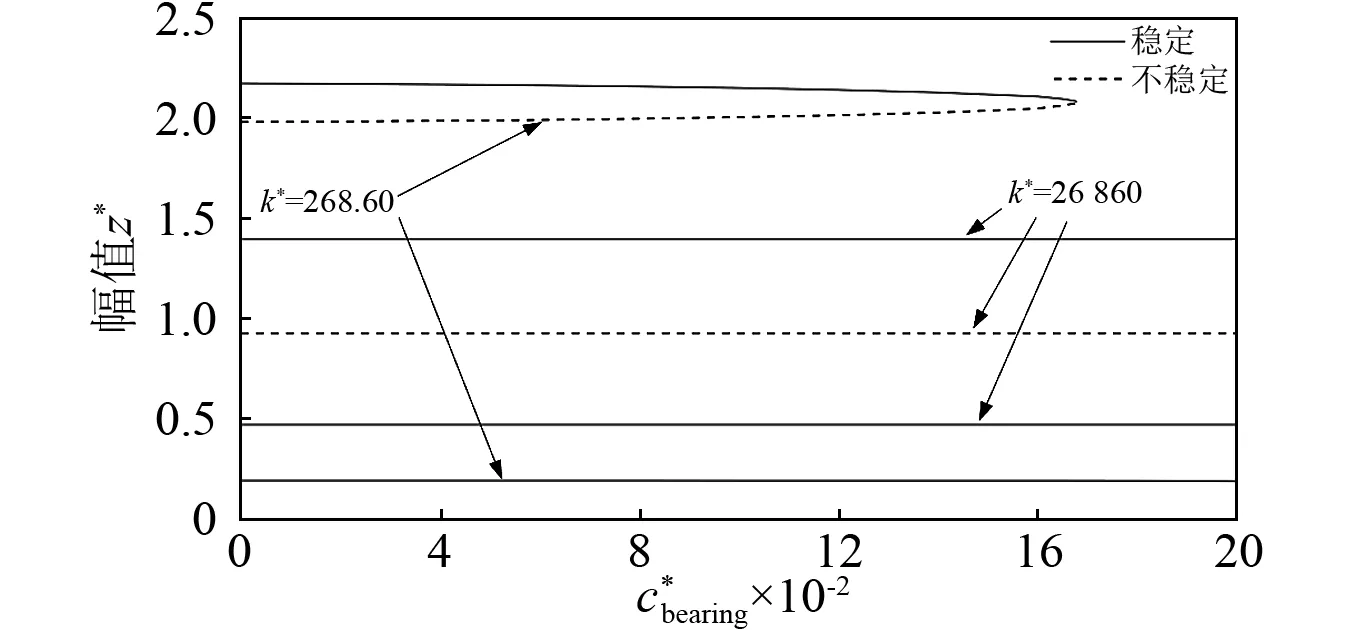
图10 轴承阻尼系数对稳态响应的影响Fig.10 Steady state responses under different bearing’s damping

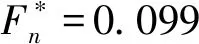
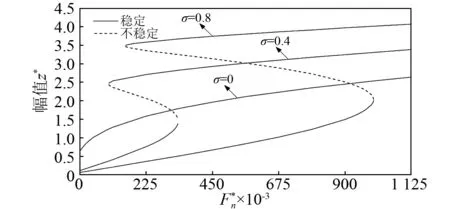
图11 碰摩力对系统稳态响应的影响Fig.11 Steady state responses under different rubbing force amplitudes μ=0.1,k*=26 860)

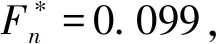
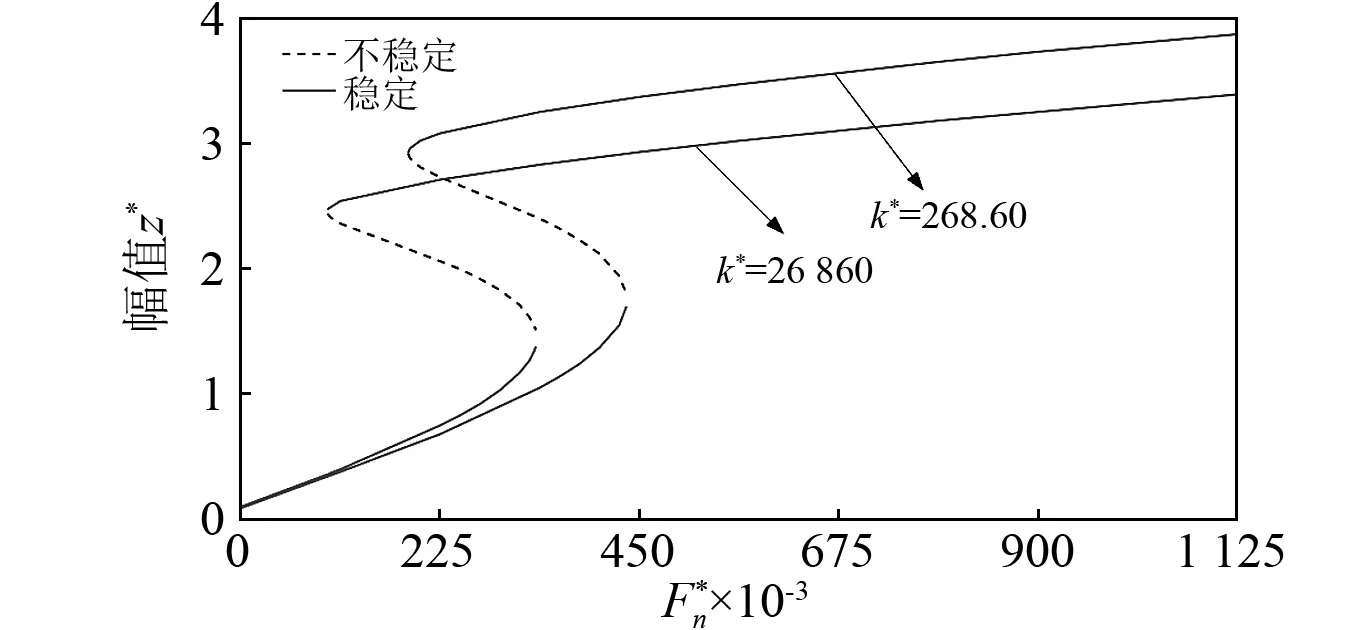
图12 不同支承刚度下碰摩力对稳态响应的影响Fig.12 Steady state responses under different support stiffness

图13描述了不同支承刚度和转轴阻尼条件下第一和第二分叉点的变化轨迹。随着阻尼的增加，两类分叉点的频率都在降低，而第二分叉点的速度更快，最终两条轨线交于一点。当实际阻尼大于该值时，将确保系统不发生分叉，达到完全稳定。从图中可知，当阻尼较小时，两个系统都会发生失稳，阻尼越小，失稳区间越大。当支承刚度较高时，需要更大的阻尼以使系统达到完全稳定。

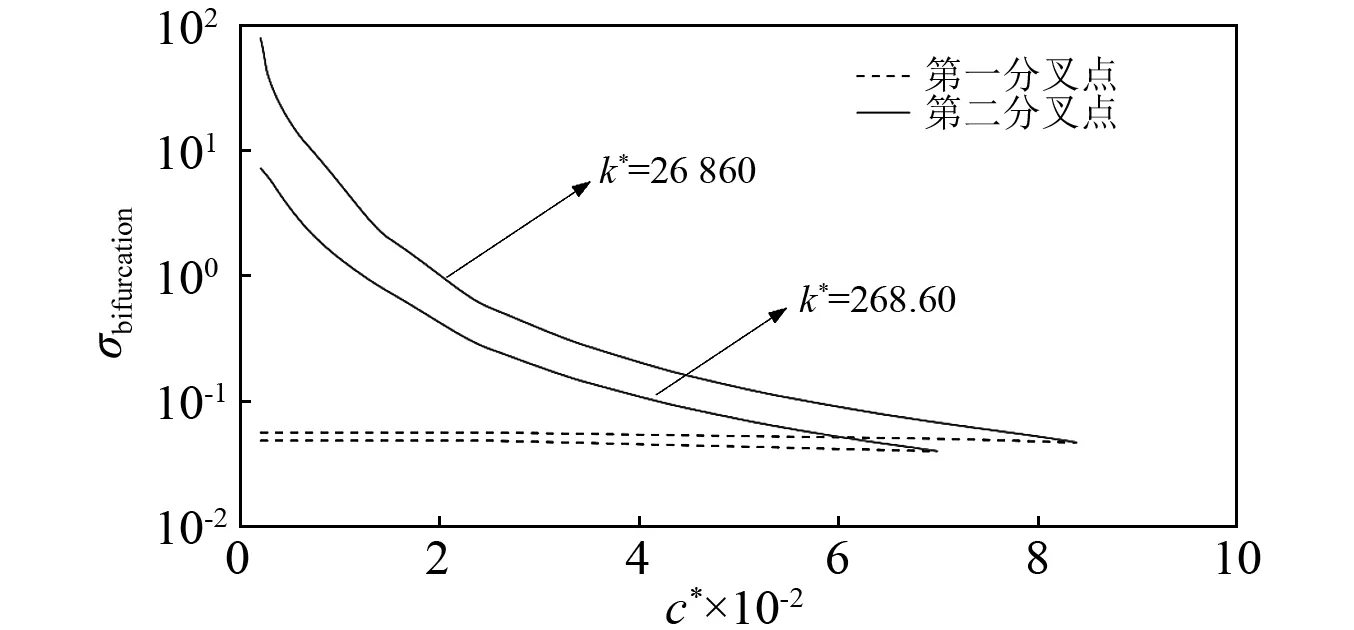
图13 第一和第二分叉点的轨迹Fig.13 Loci of the first and second bifurcatin points

4 结 论

本文基于多尺度摄动理论，研究了转子-叶片系统在主共振状态下的响应，得出的结论如下：

(1) 转子-叶片系统为硬式非线性，随着碰摩力和圆盘偏心量的增加，非线性增强，系统稳定性降低，第一和第二分叉点频率升高，跳跃频率和共振峰值升高。

(2) 随着支承刚度降低，系统非线性减弱，分叉点频率降低，共振峰值和跳跃频率随之降低。支承刚度较高时，需要更大的结构阻尼达到稳定状态。在达到二者跳跃频率之前，支承刚度较低时响应幅值较大。

(3) 随着摩擦因数的增加，系统的跳跃频率和共振峰值提高。

(4) 较小的结构阻尼会导致系统产生失稳，支承刚度较低时，轴承阻尼对系统振动幅值的影响较大。