基于黏弹性理论的碰撞力计算方法及其在碰撞TMD中的应用
张井财, 李英娜, 薛启超,2, 张春巍
(1. 哈尔滨工程大学 航天与建筑工程学院,哈尔滨 150001;2.青岛理工大学 土木工程学院,山东 青岛 266033)
地震作用下,相邻结构或构件间的碰撞和冲击常常会导致结构出现多种形式的破坏,如局部构件脱落甚至整体的坍塌。这种现象在世界上多次地震中都已经被观察到[1-3]。结构或构件间的碰撞作用会导致构件破坏,但碰撞作用过程中的能量耗散作用也可以被利用,实现对结构的振动控制。碰撞式可调谐质量阻尼器(Pounding Tuned Mass Damper, PTMD)是在传统的TMD系统上加装黏弹性材料碰撞装置,令附加质量与黏弹性碰撞装置发生碰撞,输入的能量在碰撞过程中不断耗散,实现对主体结构振动的控制[4-11]。
无论是想避免(缓解)碰撞带来的危害,还是想充分的利用碰撞耗能作用,准确地计算和分析碰撞过程中的相互作用是对碰撞问题进行研究的重要前提。
碰撞与冲击是一个传统的力学问题,经典的弹性理论忽略碰撞物体间的相互作用,以碰撞前后能量和冲量的变化来描述碰撞过程。针对碰撞物体间的相互作用,Goldsmith等[12]最先提出将单自由度碰撞过程中的接触-回复过程的作用考虑为一个线性弹簧或非线性弹簧,并成功应用于碰撞分析。在此基础上,针对碰撞过程中存在的能量耗散,加入了线性阻尼器的Kelvin模型被Anagnostopoulos[13]提出,能够有效地考虑建筑结构间碰撞过程中的能量耗散。更为复杂的碰撞力模型大都基于Kelvin模型进行改进的结果,如Muthukumar等[14]推导了包含了非线性弹簧的Kelvin模型,即Hertz-Damp模型;Jankowski[15-16]在Kelvin模型和赫兹非线性弹簧理论的基础上,将碰撞物体间的接触过程分为逼近过程和分离过程,从而消除碰撞力曲线结束位置存在的拉伸作用,该模型是目前运用最广的模型之一,如杨永强等[17-19],对相邻建筑(构件)的碰撞破坏问题的研究均采用此模型;赵大海等[20]则就隔震结构碰撞问题提出了改进Hertz-damp模型。
常用的碰撞力模型大都存在一些缺点,如模型参数缺乏具体的物理意义、适用性不强、小比例模型试验结果在应用于真实结构时理论不完善等等。为了解决这些问题,本文结合接触力学和线性黏弹性力学理论建立一种新的碰撞力模型分析方法,并根据两个典型试验和一个小型振动台试验验证了该分析方法在单次碰撞和连续碰撞情况下的有效性。
1 黏弹性基本理论
1.1 黏弹性物质的本构关系
图1是线性黏弹性固体的本构模型,图1(a)是Kelvin模型,该模型通过并联一个黏壶和一个弹簧来模拟物质的弹性和黏性性质,但是该模型无法模拟材料的瞬时弹性的性质。但对于一般材料,瞬时弹性是存在的,特别是在低速碰撞过程中材料的瞬时的弹性至关重要,于是有采用三参数模型如图1(b)。

图1 线性黏弹性物质的本构模型Fig.1 Linear viscoelastic constitutive models
对于三参数模型,分别定义σ,ε1,ε2,ε为模型总应力、Kelvin模型的应变、与之串联的弹簧的应变和模型总应变,则有
ε=ε1+ε2
(1)
(2)
σ=E2ε2
(3)
式中:E1,E2和C1为三参数黏弹性模型的参数,见图1(b)。写成三参数模型的标准形式
(4)
其中,
(5)
由弹簧、阻尼通过串、并联方式得到的更复杂的黏弹性本构关系如图1(c),本构关系可以统一写成
(6)
为便于书写,现引入微分算子
(7)
那么,以上本构关系可以统一写成
Pσ=Qε
(8)
1.2 拉普拉斯变换域内黏弹性材料的本构方程
由前文,引入微分算子后,黏弹性物质的本构方程得到了形式上的简化,但是本质上还是微分关系式,仍然不便使用。考虑到在拉普拉斯变换域内,黏弹性物质的应力应变可以转换成线性关系,该关系在形式上和原物理空间下线弹性的本构关系相同,因此可以大大简化使用过程。此时,在拉普拉斯变换域内解答一个黏弹性问题和在原物理空间下的线弹性问题是一致的(弹性-黏弹性对应原理),在求得拉斯变换域内的解后再通过逆变换即可以得到原物理空间下的解。
黏弹性材料在拉氏变换下的本构关系为

(9)
(10)
写成类似线弹性本构关系的形式
(11)
(12)
2 基于黏弹性理论的碰撞力模型
2.1 基本假设
(1)忽略碰撞区的惯性效应。土木工程领域的碰撞,应变范围约在10-4~10-2,属于传统的低速碰撞问题,因此碰撞接触区质量的惯性效应可以忽略。
(2)碰撞过程中的能量耗散只来源于材料的黏弹性性质。实际上,几乎所有材料都具备黏弹性性质,也完全可以用黏弹性模型予以描述。传统的材料如混凝土、钢材均可视为是黏弹性材料,完全线弹性材料C=0。
2.2 分析过程
具体分析流程如图2所示,首先需要对模型进行简化,再借助接触力学获得其准静态的力-位移表达式,最后通过软件(MATLAB)进行拉氏变换和逆变换获得碰撞力的时域表达式。
由接触力学理论,两物体发生碰撞后碰撞力按照式(13)计算
F=D(A,R,l)E*δα
(13)
式中:F为碰撞两者间的碰撞力;D(A,R,l)和α为考虑了碰撞两物体接触面积、接触面的曲率半径等条件的参数;δ为碰撞侵入位移;E*为碰撞两者的等效弹性模量。
将式(13)做拉普拉斯变换得到式(14)
(14)
再将式(14)进行一次拉普拉斯逆变换就得到了碰撞力时域的表达式(15)
(15)

图2 基于黏弹性理论的碰撞力分析方法分析流程Fig.2 Sketch of the proposed pounding force analysis model
3 基于黏弹性理论的碰撞力模型验证
为研究两物体之间的碰撞,不同的学者或提出或改进了诸多碰撞力模型,不同的模型有不同的计算思路和适用范围。目前运用较多的有四种:线弹性模型(Linear Elastic, LE)、非线弹性模型(Non-Linear Elastic, N-LE)、线性黏弹性模型(Linear Viscoelastic, LVE)和非线性黏弹性模型(Non-Linear Viscoelastic, N-LVE),如图3所示。本文以这四种模型作为参照模型,对比验证基于黏弹性理论的碰撞力模型的精度。

图3 已有碰撞力模型Fig.3 Pounding force models
3.1 钢-钢碰撞
3.1.1 试验概述
Goland等[21]于1959年完成该试验,是一个钢球从高处跌落与钢平面之间的碰撞,示意图如图4所示。

图4 钢-钢碰撞示意Fig.4 Model of steel-steel impact
运动方程写成式(16)
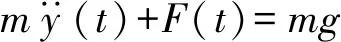
(16)
式中:m为小球质量;g为重力加速度;y为小球竖向位移,按照式(17)计算。
y(t)=δ(t)+h
(17)
式中:δ(t)为小球与钢板的侵入位移;h为试验跌落高度,本文h=5.08 cm。
由接触力学,小球和钢板间接触力按式(18)计算[22]
(18)
式中:R为小球半径,本文R=0.396 24 cm。根据黏弹性力学的对应原理,在拉氏变换域内有
(19)
再做逆变换得到
(20)

本文采用以碰撞力峰值相等的拟合方式来验证提出的模型,采用MATLAB自编循环程序拟合目前已有碰撞模型的参数,具体的循环过程如图5所示。

图5 拟合流程Fig.5 Sketch of fitting analysis
相对误差标准按式(21)计算

(21)
采用式(22)来计算各个模型的相对误差。
(22)

(23)
式中:n为采样点个数。
3.1.2 模拟结果
图6(c)是钢-钢碰撞力时程曲线。线性黏弹性模型(LE)、非线性黏弹性模型(LVE)在碰撞初期均出现了碰撞力的跳跃现象,如图6(a)所示。碰撞过程中,非线性黏弹性(N-LE)模型出现了力不连续现象如图6(b)所示,在碰撞末期,线性黏弹性模型出现了拉力,如图6(d)所示。这些均与实际碰撞过程不符。而本文模型(Proposed)没有出现上述现象,说明本文模型是符合碰撞过程实际情况的。

图6 钢-钢碰撞力时程曲线Fig.6 Time histories of pounding force of steel-steel impact
表1给出了各模型的拟合结果。由表1可知,虽然上述拟合条件能够让已有碰撞力模型保证峰值力为80.7 N,但一方面在碰撞持续时间上,线性弹性模型(LE)、线性黏弹性模型(LVE)、非线弹性模型(N-LE)和非线性黏弹性模型(N-LVE)分别为10.0 μs,8.7 μs,11.2 μs和8.4 μs,而实际碰撞持续时间为13.8 μs,各模型的碰撞持续时间误差分别是27.5%,37.0%,18.8%和39.1%,而本文模型峰值力86.0 N,持续时间11.2 μs,峰值力和持续时间相对误差只有6.2%和18.8%。而模型的相对误差Ψ为19.4%,也是所有模型中最小的。
同时,可以看出在本次试验中,本文模型和非线弹性模型(N-LE)结果接近,而两者的碰撞力-时间曲线也较接近,表明整个碰撞过程接近弹性碰撞。

表1 钢-钢碰撞各模型拟合结果
图7是各模型侵入位移和碰撞力之间的关系曲线。由图,非线性黏弹性(N-LVE)和线性黏弹性(LVE)两种模型曲线形成了滞回环,滞回环的面积即碰撞过程中的能量耗损,表明用这两种模型描述的碰撞发生了塑性碰撞,碰撞过程能量耗损比较严重,与实际情况不符。其余三种模型几乎是沿原路径返回,表明该过程是近似弹性碰撞,能量耗损较小。

图7 钢-钢碰撞力-侵入位移曲线Fig.7 Pounding force-indentation relationship of steel-steel impact
综上,本文模型可以精确合理的模拟钢-钢碰撞的整个过程,无论是峰值力、碰撞时间还是碰撞力相对误差都比现有的模型有明显优势。
3.2 混凝土-混凝土碰撞
3.2.1 试验概述
Mier等[23]于1991年完成。如图8所示,碰撞的两者分别是尺寸为0.25 m×0.25 m×20 m的混凝土预应力梁和带有圆形碰头的混凝土摆锤。摆锤强度等级B30(美标),强度38.2 N/mm2,质量570 kg,碰头处为一半径0.2 m的半球。与梁相撞时摆锤速度v1=0.5 m/s。

图8 混凝土-混凝土碰撞试验装置图Fig.8 Experimental setup concrete-concrete impact
模型简化成图9后,摆锤的运动方程为
(24)
式中:L为简化后的单摆摆长,x是摆锤水平方向的位移。

图9 混凝土-混凝土碰撞计算模型Fig.9 Model of concrete-concrete impact
3.2.2 模拟结果
图10(c)是混凝土-混凝土碰撞力时程曲线,在钢-钢碰撞中精度较高的非线弹性模型(N-LE)和线性弹性模型(LE)模拟结果和试验结果偏差都非常大。从峰值力出现时间来看,前者在4.3 ms附近,后者在5 ms附近,而试验峰值发生时间在2.1 ms附近。碰撞持时前者9 ms左右,后者10 ms左右,而试验持时只有6 ms左右。这些都表明弹性模型已经无法描述混凝土-混凝土碰撞过程。
实际上,从Mier等的试验结果来看,该过程中最大的碰撞力为100.8 kN,而按照相同接触条件下的静态加载形式,其径向侵入位移为1.3 mm左右,那么碰撞力产生的压强96.8 N/mm2左右。考虑到低速撞击时,其侵入位移要更小,那么碰撞力肯定已经超过混凝土的强度(38.2 N/mm2),换言之,混凝土摆锤碰头处已经发生劣化,存在塑性变形(图11是试验原图)。

图10 混凝土-混凝土碰撞力时程曲线Fig.10 Time histories of pounding force of concrete-concrete impact

图11 摆锤试验后破坏情况Fig.11 Damage of striker specimen
如上所述,混凝土-混凝土碰撞是一个非弹性碰撞过程,虽然黏弹性模型取得了较好的模拟效果。但是,与钢-钢碰撞试验类似,线性黏弹性模型(LVE)、非线性黏弹性模型(N-LVE)在碰撞初期均出现了碰撞力的跳跃现象如图10(a);碰撞过程中,非线性黏弹性模型(N-LVE)出现了力不连续现象如图10(b);碰撞末期,线性黏弹性模型(LVE)出现了拉力如图10(d),这些都是与实际不符的。而本文模型(Proposed)却没有出现上述现象,说明本文模型更符合碰撞过程实际情况。
图12是碰撞力和侵入位移关系曲线,线性黏弹性模型(LVE)、非线性黏弹性模型(N-LVE)以及本文模型(Proposed)均出现了滞回环,这与混凝土-混凝土碰撞过程中出现了能量耗损是相一致的。但是,前文已经证明,该碰撞过程中存在劣化现象,发生了塑性变形,而这两种黏弹性模型滞回环均没有体现这一现象,说明这两种模型仅仅是一种碰撞力上的纯数值拟合,没有考虑实际碰撞体的材料变化。相反,本文模型有明显的残余的变形,这说明本文模型与实际碰撞过程更加符合。

图12 混凝土-混凝土碰撞力-侵入位移曲线Fig.12 Pounding force-indentation relationship of concrete-concrete impact
表2是各个模型的拟合结果。由表可知,在以峰值力为100.8 kN作为拟合边界条件下,线性弹性模型(LE)、线性黏弹性模型(LVE)、非线弹性模型(N-LE)和非线性黏弹性模型(N-LVE)分别为8.8 ms,7.5 ms,10.2 ms和7.4 ms,与实际碰撞持续时间为6.1 ms相比,各模型的碰撞持续时间误差分别是44.3%,23.0%,67.2%和21.3%,而本文模型峰值力100.2 kN,持续时间7.2 ms,峰值力和持续时间相对误差只有0.8%和18.0%。在模型相对误差上,本文提出的模型误差只有12.5%,这远小于已有的其他模型,表明本文模型有更高精度。

表2 混凝土-混凝土碰撞各模型拟合结果
综上,对混凝土-混凝土这类非弹性碰撞,基于黏弹性理论的碰撞力模型依然能够很好的符合实际碰撞过程,并有足够高的精度。
4 PTMD的小型振动台试验
PTMD是一种新型的减振装置,目前对其基本性能还缺乏足够的认识,本文提出的碰撞力计算方法能否用于PTMD中也存在疑问。本节将自制小型PTMD装置,并开展小型振动台试验。一方面验证本文模型在连续碰撞过程中的有效性,另一方面验证PTMD减振有效性,给出其基本动力学性能描述,拓展本文模型的应用范围。
4.1 试验概述
试验在东北林业大学结构实验室完成(见图13)。主结构为一在顶端附有配重的钢管。圆管内径3 mm外径5 mm。PTMD结构由L型梁、PTMD配重和粘有一层黏弹性聚氨酯黏弹性体的铁环(两者共同组成振动限制器)组成。主结构总重2.5 kg,PTMD配重50 g。整个装置安装于振动台之上。振动台与控制台相连。实验的振动限制器与主结构通过一根半径2 mm的细铁棒相连,铁棒穿过主结构钢管通过螺栓紧固。铁环开有螺孔,与细铁棒之间可拆卸,通过安装不同半径的铁环即可获得不同预留间隙的PTMD。当没有铁环时,PTMD预留间隙可以认为是无限大,即PTMD退化成为TMD。由于试验条件所限,无法直接得到碰撞力曲线。本试验采用对比结构响应的方法来间接验证本文提出的碰撞力模型的精确性。

图13 PTMD的小型振动台试验装置Fig.13 Experimental setup of shake table test of PTMD
选取El地震波前10 s加速记录激励和初始位移为0.02 m的自由振动两种工况进行试验。同时为了验证本文模型,结构被简化成单自由度体系后在MATLAB/SIMILINK中进行模拟,解算方法采用四阶的龙格库塔法(OED4),时间步长0.01 s,模拟时间10 s。
试验所使用的振动台为江苏东菱振动仪器公司生产的型号ES-050-120 /LT0202的振动试验机,采用两个激光位移传感器来监测主结构质量块和配重质量块的位移响应。
4.2 试验结果
图14和图15分别是两种工况的主结构位移时程曲线,由图可得以下三点结论;
①PTMD能够有效减轻结构在El激励下的振动。PTMD可以使结构的最大位移从0.019 m下降到0.014 m(试验结果),减振率26.3%。在3~4 s和6~9 sPTMD的减振效果尤其明显。
②PTMD可以使结构在自由振动过程中快速达到静止状态。如不附加PTMD,结构位移由0.02 m下降到0.005 m需历时将近5 s,而PTMD可以将这个过程缩短至1.75 s左右(试验结果)。这表明PTMD加速了结构的能量耗散。
③试验结果(实线)和模拟结果(长虚线)虽然没有完全重合,但是整体上符合较好。说明试验结构和模拟结果是接近的。限于设备问题,无法采集碰撞力的实际情况,但是结构在振动过程中发生了碰撞,而碰撞对结构振动的影响直接的反应就是结构的振动响应,数值模拟和试验结果符合较好,说明本文提出的碰撞力模型对连续碰撞工程也是适用的,并且有足够的精度。

图14 结构在El地震波作用下的位移时程曲线Fig.14 Displacement time history excited by El wave

图15 结构具有初始位移0.02 m的自由振动位移时程曲线Fig.15 Free vibration case with an initial displacement=0.02 m
5 结 论
本文提出了基于黏弹性理论的碰撞力分析理论,推导了该方法的计算公式,给出了计算流程。根据已公开发表的钢-钢碰撞和混凝土-混凝土碰撞试验数据验证了基于黏弹性理论的碰撞力模型,并开展了自制PTMD小型振动台试验,得到以下结论:
(1)基于黏弹性理论的碰撞力模型既能够精确的描述弹性碰撞过程也能够精确的描述非弹性碰撞过程。钢-钢的碰撞是一个近似弹性碰撞的过程,混凝土-混凝土的碰撞过程中发生了劣化和塑性变形,是一个非弹性碰撞过程,本文提出的模型在峰值力、碰撞时间和相对误差方面的精度均高于现有模型。
(2)与现有模型相比,基于黏弹性理论的碰撞力模型可以获得塑性碰撞过程的残余变形,并且没有出现线性黏弹性模型在碰撞初期发生碰撞力跳跃现象和在碰撞后期的拉力现象。也不会出现非线性黏弹性模型碰撞初期碰撞力跳跃和碰撞力过程中碰撞力不连续现象。这表明本文模型能够更精确合理的描述碰撞过程。
(3)开展了自制PTMD小型振动台实验,实验结果与数值模拟符合较好,说明本文模型可以较为精确的模拟钢材与黏弹性材料之间的连续多次碰撞问题。
(4)PTMD可以有效抑制结构在外激励下结构响应,也可以加快结构在自由振动下的能量耗散,使结构快速静止。

