冗余驱动液驱振动台台阵系统内力分析及其抑制方法研究

张连朋， 杨炽夫， 杨志东， 丛大成， 韩俊伟

(哈尔滨工业大学 机电工程学院,哈尔滨 150001)

冗余驱动液驱振动台台阵系统内力分析及其抑制方法研究

张连朋， 杨炽夫， 杨志东， 丛大成， 韩俊伟

(哈尔滨工业大学 机电工程学院,哈尔滨 150001)

冗余驱动振动台台阵系统误差不仅会造成单个振动台内力，也会使振动台之间产生台阵内力,这会减小系统的净出力，甚至损坏试件。首先应用冗余驱动并联机构动力学原理，分析冗余驱动振动台台阵系统内力的形成机理；建立台阵系统的内力耦合模型，推导系统的机械安装误差、位移测量误差和伺服阀零偏三种主要误差因素与振动台内力和台阵内力的数学关系式，进而定量地分析上述误差对系统内力的影响机理。然后结合动力学关系得到振动台的内力合成矩阵和自由度广义力合成矩阵，并根据系统内力的形成机理和影响机理，分别设计了比例-积分控制器对振动台内力和台阵内力进行抑制。最后，利用SimMechanics软件建立冗余振动台台阵系统动力学模型，结合Simulink软件建立其控制系统模型并进行联合仿真验证。仿真结果表明: 该方法对台阵系统内力影响机理分析正确和提出的内力抑制方法能够有效地消除系统内力。

冗余驱动；振动台台阵；振动台内力；台阵内力；内力抑制

地震模拟振动台试验能够真实地再现各种形式的地震波形运动，是目前研究结构抗震性能最直接和最准确的试验方法，因此被广泛应用于结构的动力特性、设备抗震性能、检验结构抗震措施等方面的研究[1-2]。振动台台阵系统是由两个及以上的振动台组成，主要针对大跨度的结构试件进行振动试验，克服结构小尺寸缩尺模型所带来的试验精度问题[3-4]。目前的振动台台阵多数为单轴振动台组成的台阵系统，然而多轴振动台组成的台阵系统，更能体现试件的真实工作环境，成为振动试验的一个重要发展趋势[5-8]。

冗余驱动振动台台阵由于系统中不可避免地存在误差，必然会使系统产生冗余内力，不仅会降低系统的工作效率，而且可能损坏试件。CUI[9]提出了梯度投影法控制冗余并联机器人的冗余力。JANKOWSKI[10]提出了应用冗余力目标函数优化的方法，基于逆动力学的非线性反馈控制实现冗余机构的力位移混合控制。ZHENG[11]设计了两自由度内模控制方法，来解决6PUS-UPU实现位移力的混合控制。WANG等[12]对冗余驱动机构提出了主动位置闭环控制并通过力均衡协调控制的方法解决内力纷争问题。关广丰[14]针对冗余驱动振动台提出了压力镇定控制技术，减小振动台的冗余内力。PLUMMER[13]提出了内力耦合空间的概念，通过内力耦合空间求得系统的冗余内力，将其反馈到系统进行修正补偿。魏巍等[15-16]通过振动台的自由度空间和冗余度空间得到内力耦合空间，提出了一种基于比例控制的内力控制策略。

对于冗余驱动振动台台阵，两个振动台和试件相连接，试件相对于振动台平台静止。若两个振动台的位移不同，振动台对试件会产生力的作用，从而导致试件变形，甚至损坏试件。由于该力只是使试件产生变形，而不会对试件的运动做功，因此将这部分力称为台阵内力。目前为止，内力分析及其抑制的研究只是针对单个冗余振动台，仍无学者对于冗余振动台台阵的内力问题进行研究。

本文首先分析振动台内力和台阵内力的形成机理。考虑台阵系统的机械安装误差、位移测量误差和伺服阀零偏等因素建立台阵系统的内力耦合数学模型。根据系统内力耦合模型分别得到上述误差与振动台内力和台阵内力的数学关系表达式，进而定量地分析各种误差对系统内力的影响机理。其次，根据系统内力的形成机理和影响机理，提出采用比例-积分控制器进行相应的内力抑制从而消除系统内力，提高系统的工作效率，保护试件不受内力损坏。最后，通过仿真验证本文内力分析的正确性，并验证提出的控制策略的有效性。

1 冗余驱动振动台台阵系统描述

本文的研究对象为由两个相同的电液式地震模拟振动台组成的台阵系统，如图1所示。图1(a)为系统的主要组成框图，主要由任务管理单元、油源管理单元、液压源、控制器、信号调理单元、振动台及其附件和试件组成。任务管理单元通过RS485进行油源管理单元的控制，并通过TCP/IP协议与控制器通讯，两个控制器之间通过火线进行信号交换，通讯协议为IEEE1394。两个控制器的控制信号经过信号调理单元处理，得到指令信号控制平台按着指定的波形运动。

图1(b)为振动台台阵的结构示意图。整个台阵结构主要由十六套电液伺服驱动系统、振动台平台、反力墙和基础组成。每套驱动系统通过上铰和下铰将平台与反力墙或基础连接。两个振动平台与试件固定连接。每套电液伺服驱动系统都安装有位移传感器、加速度传感器和压差传感器。位移传感器安装在液压缸上，加速度传感器安装在平台上靠近液压缸活塞杆处，压差传感器用于测量液压缸上下两腔的压力差。

(a) 振动台台阵系统主要组成框图

(b) 振动台台阵系统结构示意图图1 振动台台阵系统Fig.1The diagram of shaking tables

每个振动台有八个相同的液压缸驱动，其中水平X向两个，水平Y向两个，垂直Z向四个，可以独立实现平台六个自由度的运动。因此，每个振动台都为冗余驱动系统。两个振动台可以单独工作，也可以作为台阵系统工作。当作为台阵系统工作时，两个振动台相互协调运动，实现被试件的指定运动。以台阵形式工作时，两个振动台之间也会由于振动台运动的位移不同步使振动台之间产生台阵内力。系统内力不仅会降低系统的工作效率，而且会对试件造成损坏。因此，有必要对振动台台阵的内力进行分析并且通过控制来消除内力。

2 振动台台阵系统内力形成机理

2.1 振动台内力形成机理

针对本文的冗余振动台台阵系统，采用牛顿-欧拉法建立单个冗余驱动振动台的动力学方程[16]

(1)

由于振动台的垂直向液压缸采用的是静力平衡缸，并且振动台的哥氏力与惯性力相比很小，因此，式(1)中的哥氏力项和重力项可以忽略,变为

(2)

求解式(2)可得

(3)

(4)

式(4)右边第二项恒为零，即

(5)

2.2 台阵内力形成机理

振动台台阵系统的单个振动台采用的是自由度控制策略，是一种平均的控制思想。平台的期望姿态为q，实际的平台的输出姿态为

(6)

式中:qo为振动台的控制姿态输出；Δ8×1为位移测量误差和机械安装误差。

两个振动台的实际输出位姿之差

(7)

由式(7)可以看出，两个振动台的实际输出位姿不同，将引起试件的变形，两个振动台之间产生相互作用力，即两个振动台的出力之差

(8)

式中:Kw为试件的刚度矩阵；fi为第i个振动台的液压缸出力，i=1,2。

式(8)输出的两个振动台的出力之差，是由于两个振动台的位姿不同引起的，该力仅引起试件的变形，对试件的运动不做功，因此称为振动台的台阵内力。

3 振动台台阵系统内力分析

3.1 台阵系统内力耦合模型

若对图1(b)所示的三向六自由度振动台台阵结构进行分析，其内力耦合数学模型及其复杂，并且其数学模型无法进行各种影响因素下内力的定量分析，只能通过建立仿真模型进行仿真分析。因此，为了方便公式的推导和更明确地对台阵系统内力进行定量地分析，将图1(b)模型进行等效简化，只分析单个运动方向的单个冗余驱动振动台组成的振动台台阵，其结构如图2所示。该模型的内力影响机理与图1(b)各个方向内力的影响机理相同，因此不影响本文分析的正确性。并且其分析的合理正确性将在本文的仿真验证中通过建立整个三向六自由度振动台台阵系统的模型进行验证。

1#和2#液压缸组成1#振动台，3#和4#液压缸组成2#振动台。假设1#液压缸存在位移测量误差为△lm，伺服阀零偏为△u1，机械安装误差为△lz，2#液压缸伺服阀零偏为△u2。2#振动台不存在误差。振动台平台质量均为2mp，刚度为Kn；试件的质量为4ml，刚度为Kw，并假设试件和振动台平台的质量由四个液压缸平均支撑。

图2 冗余驱动振动台台阵系统结构Fig.2 Schematic diagram of redundant-drive shaking tables

对于单个冗余振动台应用自由度控制策略[4,14]，振动台之间应用并行同步控制[18]。结合电液伺服控制系统[17]和图2所示的振动台台阵系统耦合结构图，得到液压振动台台阵系统的耦合控制系统模型，如图3所示。其中，fn表示1#振动台的内力，fw表示振动台之间位姿不同引起的台阵内力。

图3 振动台台阵耦合控制系统模型Fig.3 Coupling control system model of shaking tables

3.2 振动台内力分析

根据图3可得，1#液压缸和2#液压缸的控制输出位移分别为

(9)

(10)

1#振动台控制系统的反馈位移为

(11)

1#振动台控制系统的控制变量为

U=Ke(R-Lc1)

(12)

(13)

将式(13)进行转换可得

(14)

1#振动台的内力表示为

Fn=Kn(L1-L2+ΔLz)

(15)

将式(9)和式(10)代入式(15)，可得

Fn=

(16)

对式(16)进行变换，可得

Ks1ΔU1-Ks2ΔU2+sGhΔLz]

(17)

将式(14)代入式(17)可得，1#振动台的内力与机械安装误差、位移测量误差及伺服阀零偏之间的关系式如下

(18)

根据拉普拉斯终值定理，稳态时振动台内力为

(19)

稳态时，式(18)中的输入信号均为常值，此时输入信号的传递函数分别可以表示为：R(s)=r/s，ΔLc(s)=Δlc/s，ΔLz(s)=Δlz/s，ΔLm(s)=Δlm/s，ΔU1(s)=Δu1/s，ΔU2(s)=Δu2/s。将上述代入到式(18)中，结合式(19)可得：

(20)

从式(20)可以看出单个振动台的内力，与机械安装误差和位移测量误差无关，只与伺服阀的零偏有关。伺服阀可以存在零偏，只要保证△u1-△u2=0，即两个伺服阀的零偏值相同，则可以使其不影响内力的大小。内力的大小与伺服阀的零偏成正比关系。另外，也可以看出两个液压系统特性不一致时，作用于振动台的外负载力也会影响到振动台的内力。

若振动台的液压驱动系统的控制增益相同，即Ks1-Ks2=0，则式(20)变为

(21)

将式(21)所示的单自由度单冗余振动台内力推广到三向六自由度振动台中可得到

(22)

式中:fn(6×1)为振动台的内力矩阵；Kn(6×1)为振动台的平台刚度矩阵；Ks1(6×1)为1#振动台的控制增益矩阵；Ks2(6×1)为2#振动台的控制增益矩阵；Δu1(6×1)为1#振动台的伺服阀零偏矩阵；Δu2(6×1)为2#振动台的伺服阀零偏矩阵。

上述关于振动台内力的分析结果及其拓展的正确性将在后面的仿真验证章节中进行仿真验证。

3.3 台阵内力分析

当调整两个伺服阀的零偏相同时，振动台的内力为零，说明振动台内部没有力的作用，此时

l2-l1=Δlz

(23)

由式(11)和式(23)可得1#振动台的位移

l2=lc1-0.5Δlm+0.5Δlz

(24)

由于2#振动台没有误差，所以2#振动台的位移

l3=l4=lc2

(25)

由式(24)和式(25)可得由于振动台之间位姿的不同步引起的台阵内力为

fw=(l2-l3)Kw=

(lc1-lc2-0.5Δlm+0.5Δlz)Kw

(26)

由式(9)～(11)可得

Lc1=

将式(12)代入式(27)并结合式U1=U+ΔU1和U2=U+ΔU2可得

(28)

将式(28)变换可得

(29)

根据拉普拉斯终值定理可得

(30)

同理，可得2#振动台控制系统的反馈位移为

(31)

将式(30)和式(31)代入式(26)，得

Fw=

对比式(21)和式(32)可以看出，尽管系统的机械安装误差，位移传感器的测量误差不会对单个振动台产生内力，但会对台阵产生内力，并且其误差大小与内力成正比关系。

将式(32)所示的单冗余单自由度的台阵内力推广到三向六自由度振动台台阵中可得

Fw=

式中:Fw(6×1)为台阵内力矩阵；Kw(6×1)为试件的刚度矩阵；Δlz(6×1)为1#振动台的机械安装误差矩阵；Δlm(6×1)为1#振动台的位移测量误差矩阵。

上述关于台阵内力的分析结果及其拓展的正确性将在后面的仿真验证章节中进行仿真验证。

4 振动台台阵系统内力抑制方法

上节的分析为了简化推导过程并得到定量地分析结果，只是对单个自由度进行推导。为了使分析更具说服力，后面的章节论述及验证仍将针对图1(b)的三向六自由度振动台台阵系统，这也能够从另一方面验证上节的等效简化模型及分析的正确性。

根据上述的分析可知，伺服阀的零偏影响系统内力，因此可以通过调节伺服阀的零偏使振动台内力和台阵内力为零。图4为振动台台阵系统振动台内力和台振内力补偿控制策略框图。主要包括自由度控制、并行同步控制、内力抑制以及台阵系统动力学模型。建模时考虑机械安装误差、位移测量误差和伺服阀零偏等因素的影响。

图4 振动台台阵系统内力抑制方法Fig.4 Inner coupling force compensation control of shaking tables

需要说明的是，上述内力抑制的方法只是针对两个振动台静止状态时的内力抑制，即静态内力抑制。对于振动台台阵运动时产生的内力试件等因素引起的内力属于动态内力，这不是本文研究的范围，这部分将作为作者下一步需要研究的工作。另外，对于两个振动台不同自由度之间的相互影响，不再属于内力，而是相互之间的耦合力，不是本文的研究重点，因此本文也没有涉及该问题。

4.1 振动台内力抑制方法

振动台内力补偿控制量为

(34)

式中:Kcpi为振动台内力补偿比例增益；Kcii为振动台内力补偿积分增益；f为振动台各液压缸的出力。

加入振动台的内力抑制控制器后，系统的伺服阀控制变量为

u1=uc-uci=

(35)

结合式(5)和式(22)，并令其中的κ=f，可得加入内力抑制后的振动台内力为

(36)

从式(36)可以看出通过适当调节比例-积分控制器的比例增益矩阵Kcpi和积分增益矩阵Kcii就能够使fn=0，即消除振动台内力。

4.2 台阵内力抑制方法

台阵内力的抑制方法，则是根据压差传感器采集各个液压缸的压力差，结合液压缸的活塞杆有效作用面积，得到各个液压缸的出力，通过振动台的自由度力合成矩阵，计算出振动台的各个自由度的系统出力。两个振动台在相同自由度的出力之差，即为振动台之间的台阵内力，同样的补偿原理，利用比例-积分控制器，将控制补偿量补偿到伺服阀的控制变量处，通过补偿使得台阵内力为零。

台阵内力补偿控制量为

(37)

式中:Kcpw为台阵内力补偿比例增益；Kciw为台阵内力补偿积分增益；f1为1#振动台各液压缸的出力；f2为2#振动台各液压缸的出力。

加入台阵的内力抑制控制器后，系统的伺服阀控制变量为

u1=uc-ucw=

(38)

结合式(6)和式(33)，将台阵内力分为由伺服阀零偏引起的内力和由另外两种误差引起的内力

fw=fw1+fw2

(39)

(40)

(41)

结合式(7)～(8)和式(38)～(41)，可得加入内力抑制控制器后的台阵内力为

fw=

(42)

从式(42)可以看出通过适当调节比例-积分控制器的比例增益矩阵Kcpw和积分增益矩阵Kciw就能够使fw=0，即消除台阵内力。

5 结果与验证

SimMechanics[19]是一种物理建模方法，它提供了大量的对应实际系统的元件，如刚体、铰链、约束、作动器和传感器等。使用这些模块可以方便地建立复杂图形化机械系统模型，为多体动力机械系统及其控制系统提供了有效的建模分析手段，并且能够与任何Simulink的模块及其动态系统相连接进行联合仿真。

为了验证本文的分析及其控制策略，建立图1(b)所示的振动台台阵系统仿真模型，如图5(a)所示。利用Simulink软件对台阵的液压伺服系统进行建模，并搭建如图4所示的内力抑制方法模型。应用SimMechanics软件根据振动台台阵的结构参数建立其动力学模型，如图5(b)所示。两者能够无缝地结合，进行联合仿真。振动台台阵系统模型主要包括信号发生器、控制器、内力合成、阀控液压缸、台阵动力学模型等几部分。该模型的主要参数如表1所示。

5.1 仿真模型有效性验证

本节将对前面建立的振动台台阵系统仿真模型的有效性进行验证，为后面的内力分析及其抑制方法的验证提供正确的仿真平台。

由于地震模拟振动台主要应用为振动台的X,Y,Z三个方向的平动，因此，本文虽然建立的是三向六自由度振动台台阵的模型，但是本节为了减少篇幅只对三个平动方向进行仿真验证。三个平动方向如果能够按照给定的信号运动也能够证明本文的仿真模型的正确性和有效性。

(a) 振动台台阵控制系统模型

(b) 振动台台阵系统动力学仿真模型图5 振动台台阵系统仿真模型Fig.5 The simulation model of shaking tables

参数数值平台/kg5000负载质量/kg10000两平台之间距离/m12液压缸有效工作面积/m20．0075液压油密度/(kg·m-3)845伺服阀的固有频率/Hz120伺服阀的阻尼比/无0．6伺服阀额定流量L/min(7MPa压降下)400供油压力/Pa25×106油液体积弹性模量/Pa6．9×108

本节采用两种正弦和随机信号进行仿真验证。首先，同时给定X,Y,Z三个方向相同幅值、不同频率的正弦信号，幅值为1.5 mm，频率分别为4 Hz、5 Hz、6 Hz，其给定信号和响应信号曲线如图6所示。然后，同时给定X,Y,Z三个方向峰值为2 mm，频段范围为0.1～10 Hz的随机信号，其给定信号和响应信号曲线如图7所示。

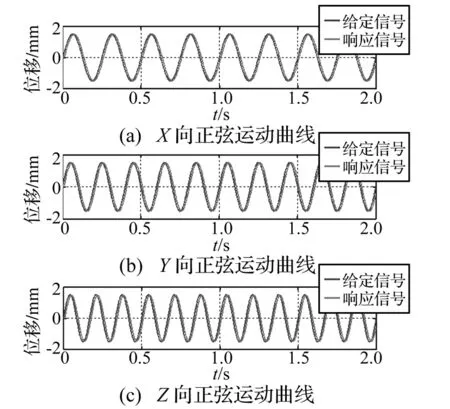
图6 振动台台阵系统正弦响应曲线Fig.6 The sine response curves of shaking tables

图7 振动台台阵系统随机响应曲线Fig.7 The random response curves of shaking tables

由图6和图7可以看出，建立的三向六自由度振动台台阵模型在X,Y,Z三个方向都能够比较好地跟踪给定的正弦信号和随机信号， 因此说明了本文建立的

仿真模型正确可行。

5.2 振动台台阵系统内力分析验证

对第3节的理论分析进行仿真验证。分别对振动台的X,Y,Z三个方向的内力分析进行验证。仿真时各个方向的仿真参数设置都相同，因此，只对其中Z向的参数进行介绍，其他两个方向设置与其相同。

仿真时系统的给定信号为0 mm的常值，只有1#振动台存在系统误差，2#振动台不存在误差。仿真分为四种工况：无任何偏差；只存在伺服阀零偏；只存在机械安装误差；只存在位移测量误差。伺服阀零偏分△u1=[0.1 0 0 0]V；△u1=[0.2 0 0 0]V；△u1=[0.1 0.1 0.1 0.1]V三种参数；机械安装误差分△l1=[1 0 0 0] mm；△l1=[2 0 0 0] mm两种参数；位移测量误差分△z1=[1 0 0 0] mm；△z1=[2 0 0 0] mm两种参数。分别对其引起的振动台内力和台阵内力进行仿真。

图8和图9分别为系统误差对振动台内力和台阵内力的影响。由图8可以看出，伺服阀的零偏为0.1 V时，振动台内力为2×104N，当零偏为0.2 V时，内力为4×104N，两者成正比关系。机械安装误差和位移测量误差对振动台的内力无影响，仅在开始时有10-4N 量级的扰动，相对于系统的出力可以完全忽略。由图9可以看出，伺服阀零偏、机械安装误差和位移测量误差对台阵内力都有影响，而且其与内力的大小都成正比关系。上述分析结果同第3节的理论分析相一致，验证了理论分析的正确性。

此外，仿真结果表明：其他两个方向的仿真结果和Z向的仿真结果基本相同，仿真曲线十分相似，因此为了减少论文的重复，只将Z向的仿真曲线列出。

图8 各种误差因素对振动台内力影响Fig.8 The errors influence to inner coupling force in shaking table

图9 各种误差因素对台阵内力的影响Fig.9 The errors influence to inner coupling force between shaking tables

5.3 振动台台阵系统内力抑制验证

内力抑制仿真试验验证，采用与5.1节中相同的仿真工况和仿真参数，以便进行更好地对比分析。

图10为加入振动台内力抑制后，系统误差对振动台内力的影响。仿真中比例增益为0.000 1，积分增益为0.001 2。对比图8和图10可以看出，加入振动台内力抑制后，伺服阀零偏引起的振动台内力能够很快地消除，并且机械安装误差和位移测量误差不会引起振动台内力，只是在初始时刻产生微小的波动。经过振动台内力抑制后，振动台的内力基本上在10-5N 量级，可以忽略。

图10 加入内力抑制控制后各种误差对振动台内力的影响Fig.10 The errors influence to inner coupling force in shaking table with compensation control strategies

图11 加入内力抑制控制后各种误差对台阵内力的影响Fig.11 The errors influence to inner coupling force with compensation control strategies

图11为加入台阵内力抑制后，系统误差对台阵内力的影响。仿真中比例增益为0.000 16，积分增益为0.001 4。对比图9与图11可以看出，加入台阵内力抑制后，三种误差因素引起的台阵内力明显地减小，基本上消除了台阵的内力。对比图10和图11可以看出，台阵内力的抑制不像振动台的内力抑制那样平稳衰减，而是振荡衰减逐渐平稳，这种现象是由于系统的控制参数设置和两种控制方式的原理不同引起的。系统平稳后，台阵内力基本上为零。从而验证了上节内力抑制方法的正确性和有效性。

此外，仿真结果表明：其他两个方向的内力抑制仿真结果和Z向的仿真结果基本相同，内力减小到可以忽略的量级，基本消除了内力，且各个方向的仿真曲线十分相似，因此为了减少论文的重复，只将Z向的内力抑制仿真曲线列出。

6 结 论

本文建立了冗余驱动振动台台阵系统的耦合模型，推导了振动台内力和台阵内力与三种主要系统误差的数学关系式。分析了振动台内力和台阵内力的形成机理，并提出相应的内力抑制方法。得到如下结论：

(1)振动台内力的大小与伺服阀的零偏大小成正比关系，与机械安装误差和位移测量误差无关。

(2)台阵内力同时受伺服阀零偏、机械安装误差和位移测量误差的影响，并且其内力大小与各个误差的大小成正比关系。

(3)应用本文提出的内力抑制方法，能够将系统的内力减小到可以忽略的量级，基本上消除误差引起的系统内力。

另外，本文只是研究系统误差对台阵系统内力的稳态影响，其对台阵系统内力的动态影响将作为作者的下一步工作，并进行深入地研究。

[ 1 ] SHEN Gang, ZHENG Shutao, CONG Dacheng, et al. Adaptive inverse control of time waveform replication for electro-hydraulic shaking table[J]. Journal of Vibration and Control, 2010(11):1611-1633.

[ 2 ] SEVERN R T. The development of shaking tables-a historical note[J]. Earthquake Engineering & Structural Dynamics, 2011, 41(2):195-213.

[ 3 ] UNDERWOOD M A. Multi-exciter testing applications: Theory and Practice[R]. Institute of Environmental Sciences and Technology, April 2002.

[ 4 ] FILIATRAULT A, WANITKORKUL A, HIGGINS P. Experimental stiffness and seismic response of pallet-type steel storage rack connectors[J]. Practice Periodical on Structural Design and Construction, 2006:161-170.

[ 5 ] 张超, 许莉, 房贞政. 三塔长跨斜拉桥振动台试验研究[J]. 地震工程与工程振动, 2013:126-132. ZHANG Chao，XU Li，FANG Zhenzheng. Research on the shaking table test of long-span cable-stayed bridge with three towers [J]. Journal of Earthquake Engineering and Engineering Vibration, 2013:126-132.

[ 6 ] 纪金豹, 李芳芳, 李振宝, 等. 地震模拟振动台台阵控制技术的研究与发展[J]. 结构工程师, 2012:96-101. JI Jinbao, LI Fangfang, LI Zhenbao,et al. Research and advances on the control technology of the multiple shaking table array system[J]. Structural Engineers, 2012:96-101.

[ 7 ] CERESA P, BREZZI F, CALVI G M, et al. Analytical modeling of a large-scale dynamic testing facility[J]. Earthquake Engineering and Structural Dynamics, 2012, 41(2):255-277.

[ 8 ] 宗周红, 陈亮, 黄云. 地震模拟振动台台阵试验技术研究与应用[J]. 结构工程师, 2011:6-14. ZONG Zhouhong, CHEN Liang, HUANG Yun. Research and application of testing technology of the earthquake simulation multiple shaking table facilities[J]. Structural Engineers, 2011:6-14.

[ 9 ] CUI Ze, WANG Xiangcan, QIAN Donghai, et al.Research on simulation of redundant robot force control[J].International Conference on Robotics and Biomimetics, 2007:1669-1674.

[10] JANKOWSKI K E, E1MARAGHY H A. Robust hybrid position/force control of redundant robots[J]. Robotics and Autonomous Systems, 1999 (27) 111-127.

[11] ZHENG Kuijing, WANG Chao. Force/position hybrid control of 6PUS-UPU redundant driven parallel manipulator based on 2-DOF internal model control[J]. Journal of Control Science and Engineering, 2014:1-6.

[12] WANG L J, MARE J C, FU Y L, et al. Force equalization for redundant active position control system involving dissimilar technology actuators[J]. Proceedings of the 8th JFPS International Symposium on Fluid Power, 2011:136-143.

[13] PLUMMER A. A general co-ordinate transformation framework for multi-axis motion control with application in the testing industry[J]. Control Engineering Practice, 2010, 18(6): 598-607.

[14] 关广丰, 熊伟, 韩俊伟. 6自由度电液振动台控制策略研究[J]. 振动与冲击,2010,29(4):200-203. GUAN Guangfeng, XIONG Wei, HAN Junwei. Control strategy of a 6-DOF hydraulic shaker[J]. Journal of Vibration and Shock, 2010,29(4):200-203.

[15] 何景峰，李宝平，佟志忠. 液压驱动冗余振动台自由度控制及内力协调[J]. 振动与冲击,2011,30(3): 74-78. HE Jingfeng, LI Baoping, TONG Zhizhong. DOF control and inner coupling force balancing of hydraulically redundant actuated shaking table[J]. Journal of Vibration and Shock,2011,30(3):74-78.

[16] 魏巍，杨志东，曲志勇，等. 超冗余多轴振动台的内力耦合控制[J]. 吉林大学学报，2015,45(5):1461-1467. WEI Wei, YANG Zhidong, QU Zhiyong, et al.Internal force coupling control for hyper-redundant multi-axis hydraulic shaking table[J]. Journal of Jilin University, 2015,45(5):1461-1467.

[17] Li Hongren. Hydraulic control system[M]. Beijing:National Defense Industry Press,1990.

[18] 邓飚, 苏文斌, 张安. 双缸电液位置伺服同步控制系统的智能控制[J]. 西安交通大学学报, 2011(45):85-90. DENG Biao, SU Wenbin, ZHANG An. Intelligent control of electro-hydraulic position servo synchronic control system with double cylinders[J]. Journal of Xi’an Jiaotong University, 2011(45):85-90.

[19] SimMechanicsTM3 Getting Started Guide[M]. Natick: The MathWorks, Inc. 2008.

Inner coupling force analysis and suppression for redundant-drive hydraulic shaking tables

ZHANG Lianpeng, YANG Chifu, YANG Zhidong, CONG Dacheng, HAN Junwei

(School of Mechatronic Engineering, Harbin Institute of Technology, Harbin 150001, China)

The table array system errors of redundantly-driven electro-hydraulic shaking tables not only lead to inner coupling force in each shaking table, but also lead to inner coupling forces between shaking tables. The inner coupling forces can reduce the net output force of the system and even may damage specimens. Here, the redundantly driven parallel mechanism dynamics was used to analyze the formation mechanism of the inner coupling force and establish the model of the inner coupling force. The mathematical relationship equations for inner coupling forces in a shaking table and those between shaking tables versus installation errors, displacement measurement errors and servo valve zero-bias of the system were derived. The influence mechanism of the errors mentioned above on the inner coupling forces was analyzed quantitatively. The inner coupling force synthesis matrix and the generalized forces of all DOFs. synthesis matrix were derived applying the dynamics relations and then the inner coupling force suppression controllers based on proportional-integral controllers were respectively designed according to the influence mechanism and the formation mechanism of the inner coupling forces. The dynamic model of a shaking table array system was built using the software SimMechanics and its control model was built using Simulink. The co-simulations were performed and the simulation results indicated that the analysis of the shaking table array system’s inner coupling forces is right and the proposed control strategies can reduce the inner coupling forces effectively.

redundantly-driven; shaking table array; inner coupling force in shaking table; inner coupling force between shaking tables; inner coupling force suppression

国家自然科学基金(51205077;51305095)

2015-05-11 修改稿收到日期：2016-01-07

张连朋 男，博士生，1988年生

杨志东 男，博士，副教授，硕士生导师，1980年生 E-mail: yangzhidong@hit.edu.cn

TH212；TH213.3

A

10.13465/j.cnki.jvs.2017.03.014