气动引力辅助的火星自由返回轨道设计方法

夏时宇，徐 波

(南京大学天文与空间科学学院，南京 210023)

0 引 言

迄今为止，人类已经成功进行了对太阳系内所有行星的无人探测和对月球的登陆探测。对载人火星探测任务的研究也逐渐升温，其中关于轨道设计的研究对于任务的成功实施具有十分重要的意义。

载人探测任务的复杂性和危险性都远远高于无人任务，对保障航天员安全返回地球提出了更高的要求。为此研究人员提出了自由返回轨道(Free return trajectory)的概念[1]。自由返回轨道是指航天器不需要自身提供变轨能量(或仅提供很少的变轨能量)，通过其他天体的借力飞行，就可以无动力返回地球，因此适合作为载人探测任务故障模式下的中止轨道。自由返回轨道可以作为航天器的初始转移轨道，如果任务正常进行，则仅需要对轨道进行少量修正即可在目标天体正常入轨，如果发生系统故障，则能够保证航天员安全返回地球。

自由返回轨道最早应用于对月球的探测，如苏联的月球3号任务和美国的阿波罗8、10、11号任务。Berry[1]对阿波罗11号任务中的自由返回轨道、发射窗口以及约束条件等问题进行了研究。黄文德等[2]基于双二体假设给出了月球自由返回轨道的设计方法，并对轨道倾角、拼接点分布等参数进行了特性分析。文献[3-4]基于圆锥曲线拼接提出了一种两段式月球自由返回轨道设计方法，具有精度高、收敛快的特点。自由返回轨道也被推广到火星探测任务的研究中。Patel等[5]在飞行时间约束和发射能量约束条件下研究了火星自由返回轨道，发现了总飞行时间分别为1.5年、2年和3年的三类自由返回轨道。李桢[6]针对载人火星探测任务，对比研究了地球-火星-地球，地球-火星-金星-地球，地球-金星-火星-地球三类自由返回轨道，并提出使用Tisserand准则进行轨道参数的初步设计。

火星自由返回轨道通常需要使用引力辅助(Gravity assist，GA)。但引力辅助技术受到借力天体的力学性质以及轨道近拱点高度约束，使得航天器双曲线剩余速度v∞偏转角度较小，加速效果有限，转移飞行时间通常较长，不利于航天器在出现故障时快速返回地球。

为解决偏转角度较小的问题，美国喷气推进实验室于1982年提出气动引力辅助(Aerogravity assist，AGA)变轨技术[7]，如图1所示，v∞-为初始双曲剩余速度， Δθ为大气飞行段转角，v∞+为经过AGA后的双曲剩余速度，φ为速度矢量偏转角。火星由于质量较小，其引力辅助能力也因此较弱[8]，使用AGA可以极大地增加速度偏转角，获得更好的加速效果，进而减少所需的借力飞行次数与飞行时间[9]。

图1 气动引力辅助示意图

气动引力辅助技术由于其可能带来的巨大收益得到了大量研究。文献[10-11]对大气飞行段进行轨迹优化，在热负载约束条件下实现最大化飞出速度。文献[12-13]设计了基于预测校正的制导算法，可以有效克服入轨误差、大气密度误差所带来的不利影响，保证气动引力辅助的可靠性和准确性。Mazzaracchio[14]设计了一种基于飞行路径角的制导算法，并指出热负载是气动引力辅助的最主要约束条件。Jesick[15]提出了一种在火星进行两次AGA的自由返回轨道，具有较小的双曲剩余速度。乔栋等[16]以探测小行星Ivar为例，提出一种将绘制等高线图和圆锥曲线拼接相结合的AGA转移轨道设计方法，该文献采用了文献[17]中提出的简化大气飞行段模型。

现有利用气动引力辅助技术的轨道设计研究中，通常将大气飞行段简化为水平飞行[9, 15-17]，而忽略了下降和上升过程，与真实的飞行过程不符。为解决这一问题，本文提出一种三段式气动引力辅助模型，将大气飞行段分为下降段、平飞段和上升段，使用大气飞行角和航迹角描述飞行过程，并建立了相应的计算模型。

本文第1节给出了自由返回轨道相关的计算模型，其中包括引力辅助模型，气动引力辅助模型和轨道优化模型。第2节分别对“地球-火星-地球”、“地球-火星-金星-地球”和“地球-金星-火星-地球”三种序列进行了轨道优化，对比了本文提出的三段式模型和现有文献中的简化模型给出的优化结果，并分析了气动引力辅助对自由返回轨道性能的影响。第3节对全文进行了总结。

1 计算模型

1.1 引力辅助模型

自由返回轨道通常采用圆锥曲线拼接方式构造。航天器在行星间转移轨道段仅考虑太阳引力，航天器相对太阳做二体运动。在借力飞行段仅考虑借力天体引力，并计算引力辅助引起的相对速度偏转角φ以及惯性系下的飞出速度V∞+，引力辅助速度矢量关系如图2所示。其中，Vp,V∞-,V∞+分别为在惯性系下借力天体以及航天器借力飞行前后的速度，v∞-,v∞+为航天器借力飞行前后的双曲线剩余速度。速度偏转角φ可用下式计算，

(1)

式中：r0为轨道近心距，μ为借力天体引力常数。引力辅助过程中没有能量消耗，因此v∞-与v∞+相等。由于r0不能小于借力天体的半径，速度偏转角φ是有上限的。

图2 引力辅助速度矢量关系

1.2 气动引力辅助模型

气动引力辅助的速度矢量关系与引力辅助类似，主要区别在于大气飞行过程会导致一部分速度损失ΔVaero，如图3所示。本节介绍三段式气动引力辅助模型以及速度偏转角φ和双曲剩余速度v∞+的计算。

图3 气动引力辅助速度矢量关系

本文提出将大气飞行段划分为下降段、平飞段和上升段，如图4所示。其中h,θ,v,γ分别为高度、大气飞行角、速度和航迹角，Δθ为航天器在各段飞过的角度。在下降段，航天器以初始状态h0,θ0,v0,γ0进入大气层并逐渐下降，经过Δθd后到达平飞高度。在平飞段，航天器保持水平飞行状态飞过Δθe。在上升段，航天器高度逐渐增大，经过Δθa后以末状态hf,θf,vf,γf飞出大气层。下面分别对这三个阶段进行计算。

图4 下降段、平飞段和上升段

1)下降段

由于下降段过程主要发生在大气密度较低的高层大气，因此可以近似认为下降段速度大小保持不变，即

v≡v0

(2)

同时根据多个文献中对气动引力辅助的仿真结果[12-14],下降段航迹角为小量且随时间近似线性变化,即

γ=at+γ0

(3)

式中:a为待求系数。

因此可以得到下降段运动方程，

(4)

(5)

式(5)中由于火星大气层高度远小于火星半径，因此可认为r≈r0。

积分式(4)得

(6)

式中:te 0为下降段结束时间，he 0为下降段结束时高度。

将γ(te 0)=0代入式(3)得，

ate 0+γ0=0

(7)

结合式(6)和式(7)可求得

(8)

将式(5)自变量换为γ得，

(9)

积分得到，

(10)

因此下降段航天器飞过的角度Δθd可由式(10)计算得到，其中h0,r0,γ0由初始状态确定，he 0可采用以下方式计算。

当航天器进入平飞状态时，由竖直方向受力平衡得，

(11)

式中:L,β,λ分别为升力加速度，航天器弹道系数和升阻比。

大气密度随高度指数分布，即

(12)

式中:ρ0,hs分别为参考大气密度和密度标高。

将式(11)代入式(12)得到进入平飞状态时的高度，

(13)

2)平飞段

航天器速度的减小主要发生在平飞段，其速度减小可通过文献[9]中模型计算，计算方式如下，

(14)

式中:D为阻力加速度，将式(14)代入式(5)并取γ=0，得到速度随大气飞行角的变化，

(15)

将式(11)代入式(15)，得

(16)

由于航天器处在平飞状态，gr为常数，可近似取火星表面处数值。积分式(16)可得平飞段末速度与飞过的角度Δθe之间的关系，

(17)

相应的双曲线剩余速度关系为

(18)

3)上升段

上升段的计算与下降段类似，可以看作下降段的逆过程，即

(19)

式中:hf=h0,rf=r0，飞出大气层时的航迹角可近似为γf=-γ0，vf可通过式(17)计算。

4)速度矢量偏转计算

气动引力辅助过程中双曲剩余速度矢量大小的减小可以通过式(18)计算得到。而速度矢量的偏转角关系如图5所示，其中δ-,δ+分别为v∞-,v∞+与大气边缘的夹角。Δθd,Δθe,Δθa分别为下降段、平飞段和上升段飞过的角度。

图5 气动引力辅助速度偏转角

从图5几何关系可以看出，气动引力辅助过程中总速度偏转角为，

φ=δ-+Δθ+δ+=δ-+Δθd+Δθe+Δθa+δ+

(20)

式中:δ-,δ+可通过经典轨道力学计算得到，

(21)

式中:e,f为双曲线轨道的偏心率和航天器的真近点角，可使用以下公式计算，

(22)

将航天器进入大气以及飞出大气时的v,r,γ代入即可计算得到δ-,δ+。

1.3 轨道优化模型

对于自由返回轨道，航天器从地球出发，经过N次借力飞行最终返回地球。因此进行轨道优化时，最小化目标函数为

(23)

对于引力辅助的自由返回轨道，优化变量取为t0,t1,…,tN,tN+1;r1,…,rN。其中，t0,tN+1分别为地球出发和返回时间；t1,…,tN和r1,…,rN为到达各借力天体的时间和近心距。

约束条件为

(24)

即地球出发时间t0在2033年到2036年范围内，各天体处近心距应至少高于天体半径200 km，且双曲剩余速度在引力辅助前后不改变大小。

对于气动引力辅助的自由返回轨道，优化变量取为t0,t1,…,tN,tN+1; Δθ1,…,ΔθN;γ1,…,γN。其中,Δθ1,…,ΔθN和γ1,…,γN分别为各借力天体处大气飞行角和进入大气时的航迹角。

约束条件为

(25)

2 轨道优化结果

本节研究了“地球-火星-地球(E-M-E)”、“地球-火星-金星-地球(E-M-V-E)”和“地球-金星-火星-地球(E-V-M-E)”三种火星自由返回轨道序列。金星的质量和轨道特性使其成为载人火星任务的首选引力辅助天体[6]，因此在后两种序列中，利用了金星引力辅助实现自由返回轨道。研究中分别对比了采用引力辅助模型、本文提出的三段式气动引力辅助模型和现有文献中简化气动引力辅助模型[17]的优化结果。

2.1 E-M-E序列

E-M-E序列只需要一次借力飞行，是最简单的火星自由返回轨道。航天器从地球出发，进入火星转移轨道。如果任务正常进行，则可以在火星近拱点处减速，进入环火轨道。如果任务终止，则不进行减速制动，直接返回地球。根据第1.3节优化模型搜索得到的燃料最优自由返回轨道如图6所示。

图6 E-M-E自由返回轨道

转移轨道参数比较见表1，其中GA为采用引力辅助的轨道，AGA1为采用三段式气动引力辅助模型的轨道，AGA2为采用简化气动引力辅助模型的轨道。

对比GA和AGA1轨道可以发现，使用气动引力辅助可以将飞行总时间减少125 d，其中返航时间可以减少102 d，因此非常适合需要快速返回地球中止轨道任务，同时燃料消耗减少约2.5 km/s。对比两种轨道的V∞速度，可以发现V∞E1基本保持不变，V∞M增大了1.21 km/s，而V∞E2减小了3.31 km/s。

对比AGA1和AGA2轨道可以发现，根据本文提出的气动引力辅助模型计算得到的轨道与现有模型计算得到的轨道参数基本一致，验证了本文模型的正确性。两个轨道的主要区别在于AGA1轨道的大气飞行角ΔθM比AGA2轨道大23°，这主要是由于简化模型中没有考虑下降段与上升段对大气飞行角的贡献。同时AGA1轨道还给出了大气飞行段的初始航迹角，可作为高精度气动引力辅助仿真的初始值。

表1 E-M-E自由返回轨道参数Table 1 Parameters of E-M-E free return trajectory

E-M-E自由返回轨道燃料消耗以及V∞速度较大，对火箭运载能力的要求较高，但由于具有出航和返航时间较短的优势，很适合作为载人任务的轨道。

2.2 E-M-V-E序列

E-M-V-E自由返回轨道到达火星后并不直接返回地球，而是相继经过火星和金星两次引力辅助后返回地球。根据第1.3节优化模型搜索得到的燃料最优自由返回轨道如图7所示。

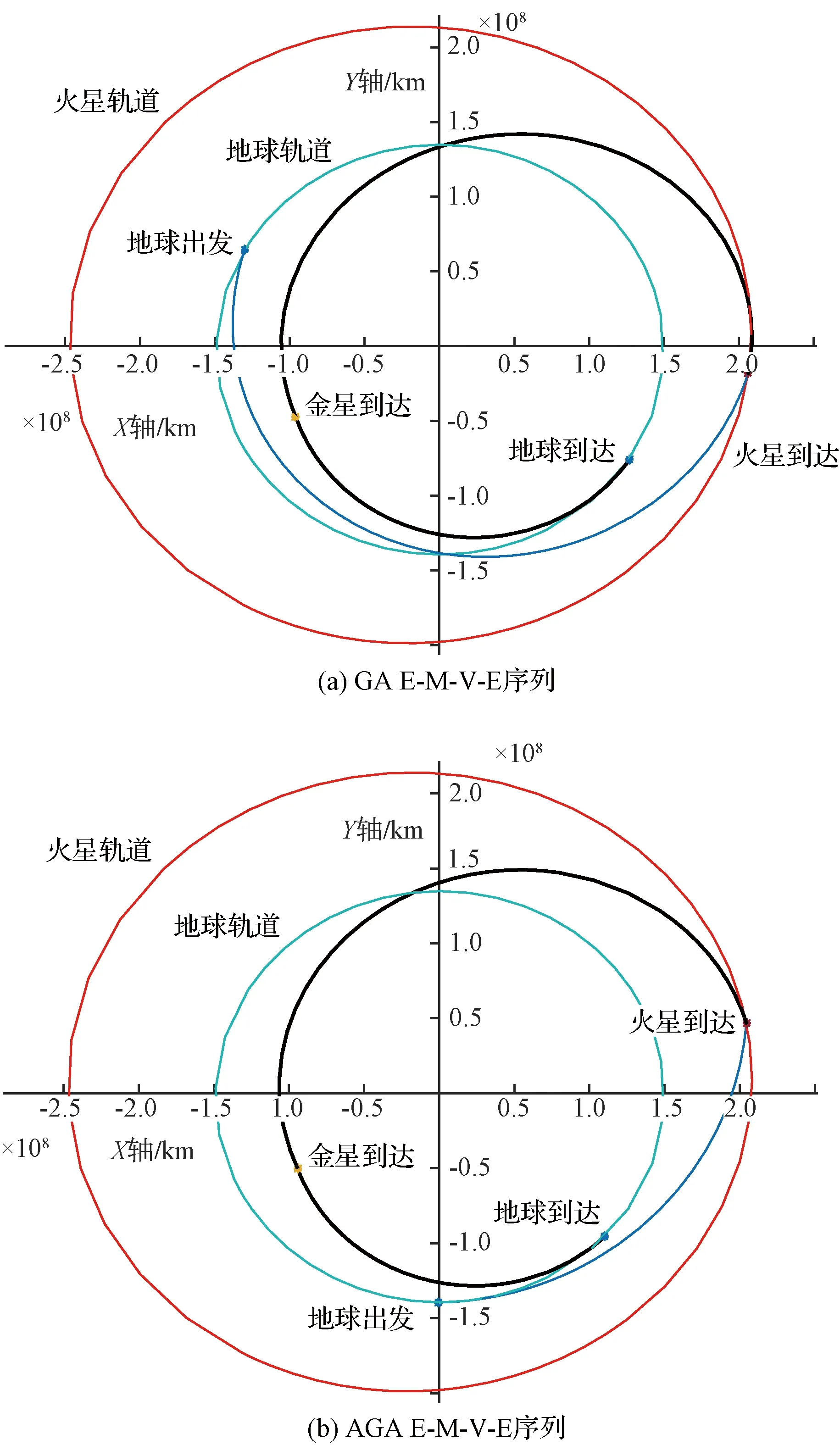
图7 E-M-V-E自由返回轨道

转移轨道参数比较见表2，其中GA为采用引力辅助的轨道，AGA1为采用三段式气动引力辅助模型的轨道，AGA2为采用简化气动引力辅助模型的轨道。

对于E-M-V-E自由返回轨道，AGA1在燃料消耗减少1.28 km/s的基础上，总飞行时间减少132 d。地火转移时间减少89 d，降低约43%，极大地加快了出航过程。由于到达火星时与火星轨道速度夹角较大，如图7所示，其V∞M也较大，不利于在火星正常入轨。

AGA轨道在火星处使用了气动引力辅助技术，而在金星处则仅使用引力辅助。这是由于金星的引力辅助能力较强，可以达到指定的速度偏转角，如果使用气动引力辅助，反而会导致速度降低，增加燃料消耗。

表2 E-M-V-E自由返回轨道参数Table 2 Parameters of E-M-V-E free return trajectory

与第2.1节类似，AGA1与AGA2轨道优化结果基本一致，其中AGA1轨道由于包括下降段和上升段，大气飞行角比AGA2轨道大。

由于使用了两次引力辅助，E-M-V-E序列相对E-M-E序列更加复杂，返航时间也更长，不利于故障模式下航天器快速返回地球。但由于其燃料消耗较少，出航时间较短，地球出发和到达V∞速度较低，有利于工程实现。

2.3 E-V-M-E序列

E-V-M-E序列与E-M-V-E序列类似，同样使用金星引力辅助，区别仅在于到达火星与金星的先后顺序，因此其优化过程也与E-M-V-E序列类似。搜索得到的燃料最优自由返回轨道如图8所示。

图8 E-V-M-E自由返回轨道

两条转移轨道参数比较见表3。其中GA为采用引力辅助的轨道，AGA1为采用三段式气动引力辅助模型的轨道，AGA2为采用简化气动引力辅助模型的轨道。

表3 E-V-M-E自由返回轨道参数Table 3 Parameters of E-V-M-E free return trajectory

由表3可知，AGA1在燃料消耗减少约2.4 km/s的基础上，相对于GA轨道飞行总时间仅减少27 d，效果不如之前两种序列。这主要是由于金星较强的引力辅助能力使航天器进入较为理想的转移轨道。

AGA1轨道与AGA2轨道参数基本一致，主要区别在于大气飞行角的不同，这与前两节的结论是一致的。

E-V-M-E序列出航时间较长，不利于正常任务的进行，但其较短的返航时间和较小的出发和返回双曲剩余速度对于故障模式下快速返回地球十分有利，同时其燃料消耗是三种序列中最小的。

3 结束语

本文对基于气动引力辅助的火星自由返回轨道进行了研究。针对现有研究中气动引力辅助模型过于简化，提出将大气飞行过程分为下降段、平飞段以及上升段三个阶段，使用大气飞行角Δθ和航迹角γ来描述气动引力辅助过程，并分别建立了各段的计算模型。

本文分别对E-M-E,E-M-V-E和E-V-M-E三种火星自由返回轨道序列进行了计算分析，比较了引力辅助模型、三段式气动引力辅助模型以及简化气动引力辅助模型。计算结果表明，根据本文提出的气动引力辅助模型计算得到的转移轨道与现有文献结果类似，主要区别在于大气飞行角的大小。现有文献模型由于忽略了下降段和上升段，其大气飞行角被明显低估，而本文提出的模型由于更接近真实的飞行过程，可以更准确地计算出大气飞行角并给出相应的航迹角。该模型还给出了大气飞行段的初始航迹角，可作为高精度气动引力辅助仿真的初始值。计算结果同时表明，对于三种自由返回轨道序列，气动引力辅助技术可以显著提升自由返回轨道性能，如降低出航和返航时间，降低燃料消耗等。虽然气动引力辅助由于其技术上的复杂性而未能在以往的航天任务中得到应用，但随着航天技术的不断进步，这种技术必将得到更广泛的应用。