应对机动目标的全捷联导弹制导控制一体化设计
赵 斌,朱传祥,徐思勇,蒋瑞民,张 琳,周 军
(1. 西北工业大学精确制导与控制研究所,西安 710072;2. 西北工业大学机电学院,西安 710072;3. 中国运载火箭研究院首都航天机械公司,北京 100076)
0 引 言
近年来,制导武器不断向低成本和高性能方向发展,由此衍生了具有代表性的两个研究热点:全捷联探测制导技术和制导控制一体化技术。
全捷联探测制导体制去除了传统平台式导引头的框架结构,减小了导引头体积、降低了研制成本,同时提高了抗过载冲击能力及可靠性[1];制导控制一体化设计能够建立起制导系统和控制系统的有机协调,相比传统的独立设计的方法,一体化设计在减小需用过载、降低脱靶量、提高可靠性与稳定性等方面具有明显优势[2]。因此,将这两者相结合,在全捷联体制下开展制导控制一体化研究对发展低成本、高性能战术导弹技术具有重要的意义。
当前一般是基于惯性系视线角速率开展制导控制一体化设计[2-7]。在全捷联制导体制下开展制导控制一体化设计同样以经典的导弹姿态动力学和弹目相对运动学为基础[8],然而全捷联体制下的光学系统、探测器与弹体固连,这也给制导控制一体化设计带来了新的问题——导引头视场角约束问题。
传统导弹的姿态运动与制导探测通过导引头框架实现隔离,具有高动态特性的导引头伺服框架用于实现对目标的锁定和跟踪[9];在全捷联体制下,一方面导弹需要不断调整姿态改变所受到的力矩和力以实现精确打击,另一方面由于弹体与探测器固连,弹体在调整姿态建立攻角时更容易引起弹目体视线角超出导引头视场角范围[10-11]。因此在全捷联制导体制下开展制导控制一体化设计时必须兼顾弹目体视线与导引头视场角之间的约束,这种矛盾在拦截机动目标时尤为突出。这使得现有的制导控制一体化方法难以直接应用[2-7]于此类对象。
针对制导控制系统存在的导引头视场角约束问题,现有研究主要集中于制导律设计,如基于比例导引的方法[12-14],基于最优控制的方法[15-16]以及滑模变结构方法[17-18]等。这些方法在建模时忽略了弹体姿态运动特性,即假设飞行攻角近似为零,由此视线角被定义为弹体速度方向和弹目视线方向的夹角。然而,实际大气层内的全捷联导弹主要是通过调整弹体姿态建立攻角以实现法向过载的跟踪,由此看来攻角为零的假设显然是不合理的。
由以上分析可知,传统制导控制一体化设计方法没有考虑全捷联体视线角约束,而考虑体视线约束的制导方法却在模型环节进行了不合理的简化。为此,本文作者在文献[11]中初步提出了一种考虑捷联视场角约束的制导控制一体化设计方法,该方法基于障碍Lyapunov函数[19]以及跟踪微分器[20]进行一体化制导控制规律的设计,然而其并没有给出严谨的稳定性证明,并且只适合于攻击静止目标。
在该项研究基础上,本文以全捷联导弹攻击运动目标为背景,提出一种满足全捷联体视线角约束的制导控制一体化方法。首先,建立了考虑体视场角约束以及目标机动的制导控制一体化设计模型;其次,基于积分型障碍Lyapunov函数[21]与动态面方法设计了一体化制导控制律,解决了视场角约束问题;针对目标未知机动以及气动参数不确定性,提出一种新型干扰观测器并将干扰估计的平方信息引入控制方程中,有效避免引入符号项,解决了变结构控制的“颤震”问题;最终基于Lyapunov稳定理论证明了整个系统的稳定性和有界收敛特性。
1 数学建模
将目标视为质点,考虑导弹的姿态和速度方向,给出纵向平面中弹-目相对运动关系如图1所示。

图1 全捷联导弹-目标二维相对运动示意图
图1中,XOY为惯性坐标系;M,T分别代表导弹和目标;AM,AT分别为导弹与目标的加速度,其方向分别与导弹和目标的速度VM,VT方向垂直;R为弹目相对距离;qL为惯性系视线角;θM,θT分别为导弹与目标的航迹角;Mxb为弹体纵轴方向,由此得到ϑ为弹体俯仰角,qBL为相对弹体系的体视线高低角。
1.1 相关假设
不失一般性,本文在进行全捷联制导控制一体化建模与制导控制算法设计过程中引入如下假设:
假设1. 在短暂的末制导过程中,假设导弹与目标速度大小保持不变。
假设2. 目标加速度、气动不确定及其微分大小是有界的。

1.2 全捷联制导控制一体化设计建模
由图1可建立起全捷联制导控制一体化设计模型,主要由全捷联导引头解耦模型、弹目相对运动模型以及弹体姿态控制模型等三部分模型构成。
1) 全捷联导引头解耦模型
由图1可知,弹体俯仰角、体视线高低角和惯性系视线高低角满足如下关系:
qBL=qL-ϑ
(1)
对其求取微分可得:
(2)
其中,Δ1=-ωz。
2) 二维非线性弹目相对运动模型[22]
(3)
对于轴对称战术导弹而言,弹体纵向加速度用气动力系数近似表示如下:
(4)

由式(3)和式(4)可知:
(5)
其中,

3) 纵向平面线性化姿态控制模型[23]
(6)
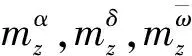
通常战术导弹在末制导阶段是无动力飞行,即P=0。定义如下模型参数:
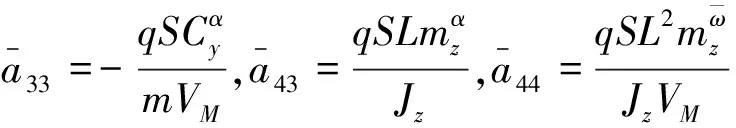
由此可对式(6)进行简化:
(7)
(8)
对于稳定飞行的战术导弹,其攻角、舵偏角及角速率都是有界的,并且气动参数摄动也是有界的,结合假设1和假设2可知不确定性及其微分都有界

(9)
其中,Ei,Di(i=1,2,3,4)分别是未知的不确定性上界以及不确定性的微分上界。
本文的设计目标是设计一体化制导控制律u,使得系统(8)在不确定性(9)作用下渐进稳定收敛,同时系统体视线角状态满足物理视场角Q的约束,即
|x1| (10) 由式(10)可知,本文受约束的状态即为x1,在设计过程中应尽可能保证体视线角比较小,因此其需要跟踪的指令xd=0,由此满足假设3的条件。 引理1[21]. 定义积分障碍Lyapunov函数(iBLF) (11) 其中,z=x-xd为跟踪误差,|x| 1) 若状态满足|x| (12) 2) 函数V(z,xd)对xd的偏导数可表述如下: (13) 引理2[24]. 对于实数m,n≥0,p,q>1,若其满足等式1/p+1/q=1,则如下不等式成立: (14) V→∞,当|x|→kc时 基于动态面控制,全捷联一体化制导控制规律设计步骤如下: 1)设计x2的虚拟控制律 定义误差变量s1=x1-x1d,x1d=0,结合式(9)可得s1的微分如下: (15) 以x2作为虚拟控制量,设计x2c为 (16) 为了设计非线性干扰观测器,设计中间变量为 z1=d1-κ1s1,κ1>0 (17) 结合式(15),对式(17)进行微分可得: (18) 设计变量z1的自适应律如下: (19) 根据式(17)可设计干扰观测器如下: (20) 基于动态面控制思想,为了避免虚拟控制微分膨胀,引入一阶滤波器获取新的变量x2d (21) 2)设计x3的虚拟控制律 定义新的误差变量为s2=x2-x2d,结合式(9) 可得s2的微分如下: (22) 以x3作为虚拟控制量,设计x3c为 (23) 类似式(17)~(20),设计干扰观测器如下: (24) (25) 同样引入一阶滤波器获取新的变量x3d (26) 3)设计x4的虚拟控制律 定义新的误差变量为s3=x3-x3d,结合式(9) 可得s3的微分如下: (27) 以x4作为虚拟控制量,设计x4c为 (28) 同样设计干扰观测器如下: (29) (30) 引入一阶滤波器以获取新的变量x4d (31) 4)设计一体化制导控制律u 定义新的误差变量为s4=x4-x4d,结合式(9) 可得s4的微分如下: (32) 由此可以设计控制律u为 (33) 类似式(17)~(20),设计干扰观测器如下: (34) (35) 定义上述推导过程的边界层误差变量为 yi=xid-xic,i=2,3,4 (36) 将式(21)、(26)、(31)代入式(36)并结合假设3可知 (37) 根据引理2可知: (38) 定义中间变量的自适应律估计偏差如下 (39) 根据干扰观测器(20)、 (24)、 (29)、 (34)可知估计误差的导数为 (40) 定义干扰观测器估计误差为 (41) 由此可知: (42) 将式(36)代入式(15)、 (22)、 (27)、 (32)和(36)可得: (43) (44) 定理1. 对于捷联制导控制一体化系统(8),采用控制器(33),如果系统初始体视线角满足|x1(0)| 1)系统状态的跟踪误差最终稳定收敛至有界集合内。 2)受限状态x1始终满足体视线约束|x1| 3)闭环系统所有信息均一致有界。 证. 为了确保体视线高低角满足式(10)的约束,设计积分型障碍Lyapunov函数如下: V=V1+V2+V3+V4 (45) 其中,各个变量定义如下: (46) (47) (48) (49) 根据引理1对式(45)求导可得: (50) 分别将式(37)、(40)和(44)代入式(50)可得: (51) (52) 进一步可得: (53) 同时还能得到: (54) 将式(52)~(54)代入式(51)可得如下不等式成立: (55) 根据式(12)可知: (56) 选择参数L,D>0,使得: (57) 则可得如下不等式成立: (58) 对式(58)进行积分可得: (59) 1) 末制导开始时刻目标处于导引头视场范围内,即|x1(0)| (60) 因此根据式(59)容易得到: (61) 2) 式(58)则表明整个系统运动过程中V是有界的,并且初始时刻|x1(0)| 3) 根据结论1~2及引理3可知,系统状态、跟踪误差有界;在此基础上根据式(16)、(23)、(28)和(33)可知,所有虚拟控制量及一体化制导控制信号都是有界的,即闭环系统所有信息均一致有界。 注1. 导弹捷联导引头通常存在盲区,当弹目距离小于一定数值时导引头输出信息无效,此后导弹惯性飞行直至命中目标。对于激光半主动导引头而言其盲区实测结果通常约为10~40 m,由此可知式(57)中与相对距离R相关的k2,τ2不存在奇异问题。 注2. 本文使用干扰观测器对不确定性进行估计,并且将其平方信息引入设计过程,避免符号项的使用,由此综合得到了光滑的虚拟控制规律及最终的一体化导引控制规律。 以某型导弹为例进行仿真校验,导弹参数、IGC控制参数及初始场景设置分别见表1、表2和表3。 表1 导弹参数Table 1 The missile parameters 场景1:At=20sin(2πt)m/s2,视场角约束分别为8°,8.5°和9°,标称气动下的结果见图2~图5。 场景2: 目标方波机动,机动加速度幅值为At=20 m/s2,视场角约束设置为8°,得到的干扰估计结果如图6所示。 场景3:At=20sin(2πt)m/s2,视场角约束分别设置为8°,气动拉偏下的仿真结果如图7所示。 表2 控制参数Table 2 Parameters used in the control algorithm 图2 体视线角曲线 图3 舵偏角曲线 不同场景下的仿真脱靶量总结于表4中。从表4可以看出,不同场景下均能实现对目标的精确拦截。此外,从图2~图7还可以得到的以下结论: 1) 从图2可以看出,三种不同视场角约束均能满足要求,符合文中定理1的结论2;从图3的局部可以看出,视场角约束越严格,所得到的精确打击末端的舵偏角越大,并且所得到的舵偏角光滑并且非奇异,这与式(33)的数学特性相一致;从图4和图5可以看出,不同视场角约束下,虚拟控制量跟踪误差和动态面的边界层误差均快速收敛至零附近邻域内,符合文中定理1的结论3。 图4 虚拟控制跟踪误差 图5 边界层误差 图6 干扰观测器估计 图7 气动拉偏仿真结果 2) 从图6可以看出,干扰观测器估计工作状态良好,能够实现对不确定性的精确估计。 3) 从图7可以看出,针对气动偏差带来的不确定性,本文所提出的一体化制导控制规律依然能够有效应对,其原因是干扰观测器对系统的总和扰动进行了估计,然后在控制律中对其进行了有效补偿。 表3 初始仿真场景Table 3 Initial simulation scenario 表4 仿真结果Table 4 Simulation results 将式(46)中的iBLF替换为式(62)所示的二次型Lyapunov函数,可得到传统的一体化控制律如式(63)所示,其他过程控制量及干扰观测器设计不变。 (62) (63) 将本文方法和传统方法分别记为iBLF-IGC和QLF-IGC,选择同样的控制参数和初始场景进行仿真。从图8可以看出,视场角为±7°的条件下,传统方法的体视线角不满足约束条件,而本文所提方法则可以一直保证±7°视场约束。 图8 与传统方法的对比结果 全捷联导引头探测器与弹体固联,使其视线测量与姿态运动强烈耦合,针对此问题本文提出了一种考虑视场角约束的制导控制一体化设计方法。 该方法采用非线性干扰观测器可以实现对目标机动与气动扰动带来的模型不确定进行在线精确估计,并将估计值的平方引入动态面设计中;采用积分型障碍Lyapunov函数进行虚拟控制设计可以有效解决视场角约束问题;通过Lyapunov稳定性定理可以证明闭环系统的有界稳定特性。2 捷联制导控制一体化设计
2.1 相关引理
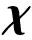

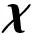
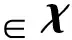
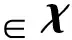
2.2 全捷联制导控制一体化设计

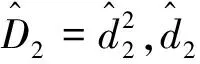
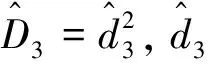
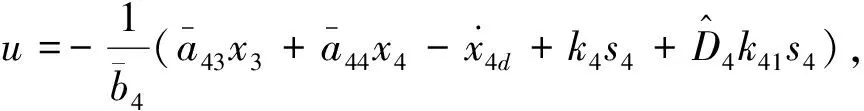

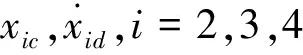
2.3 稳定性分析
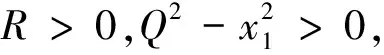

3 仿真校验

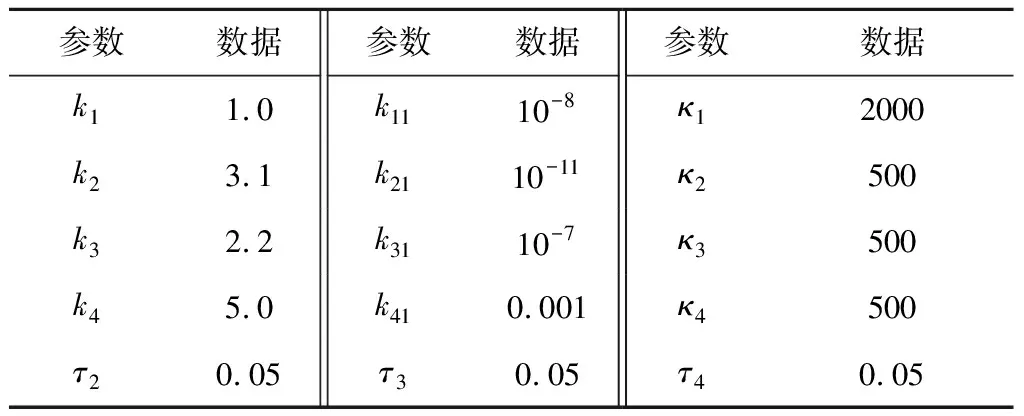
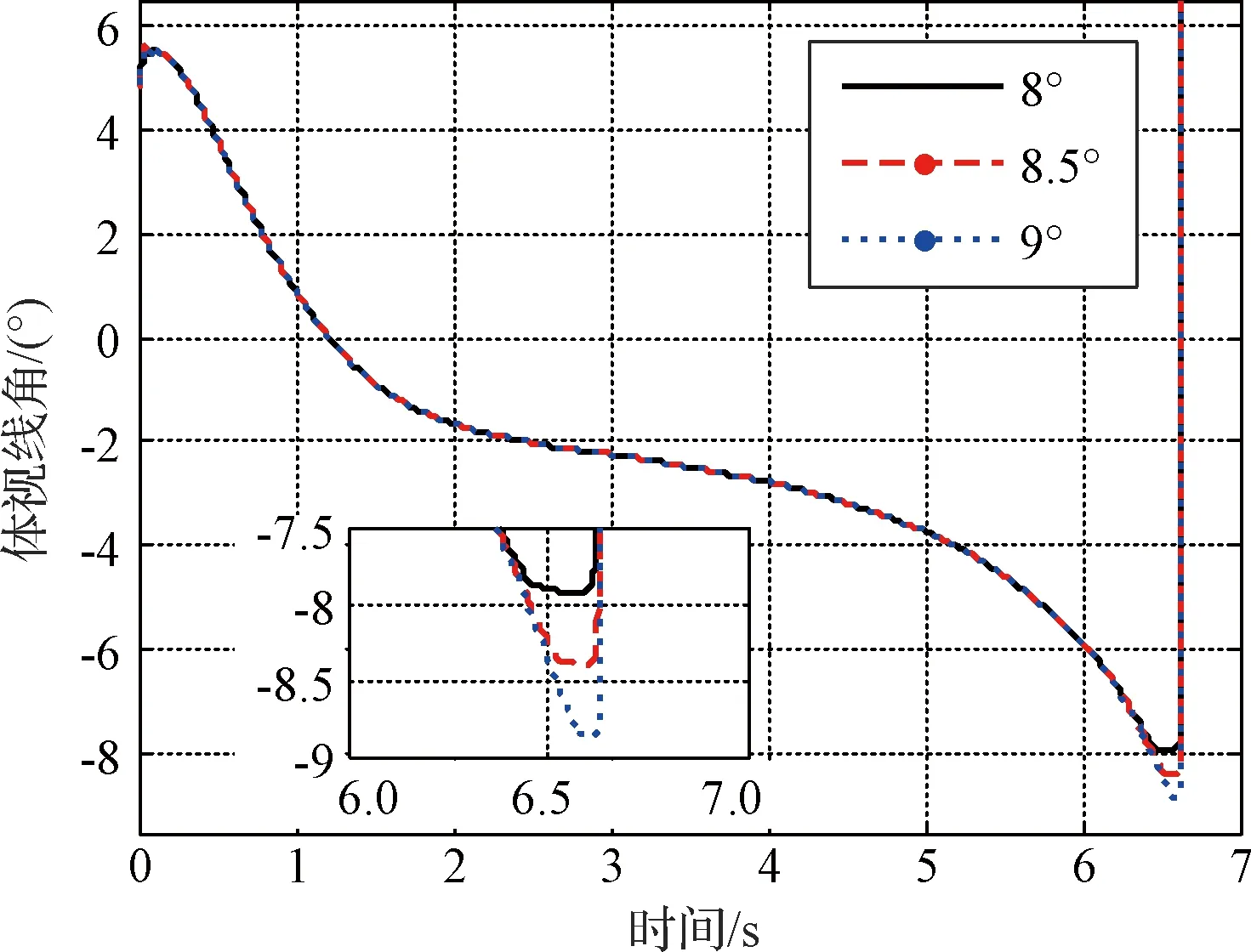
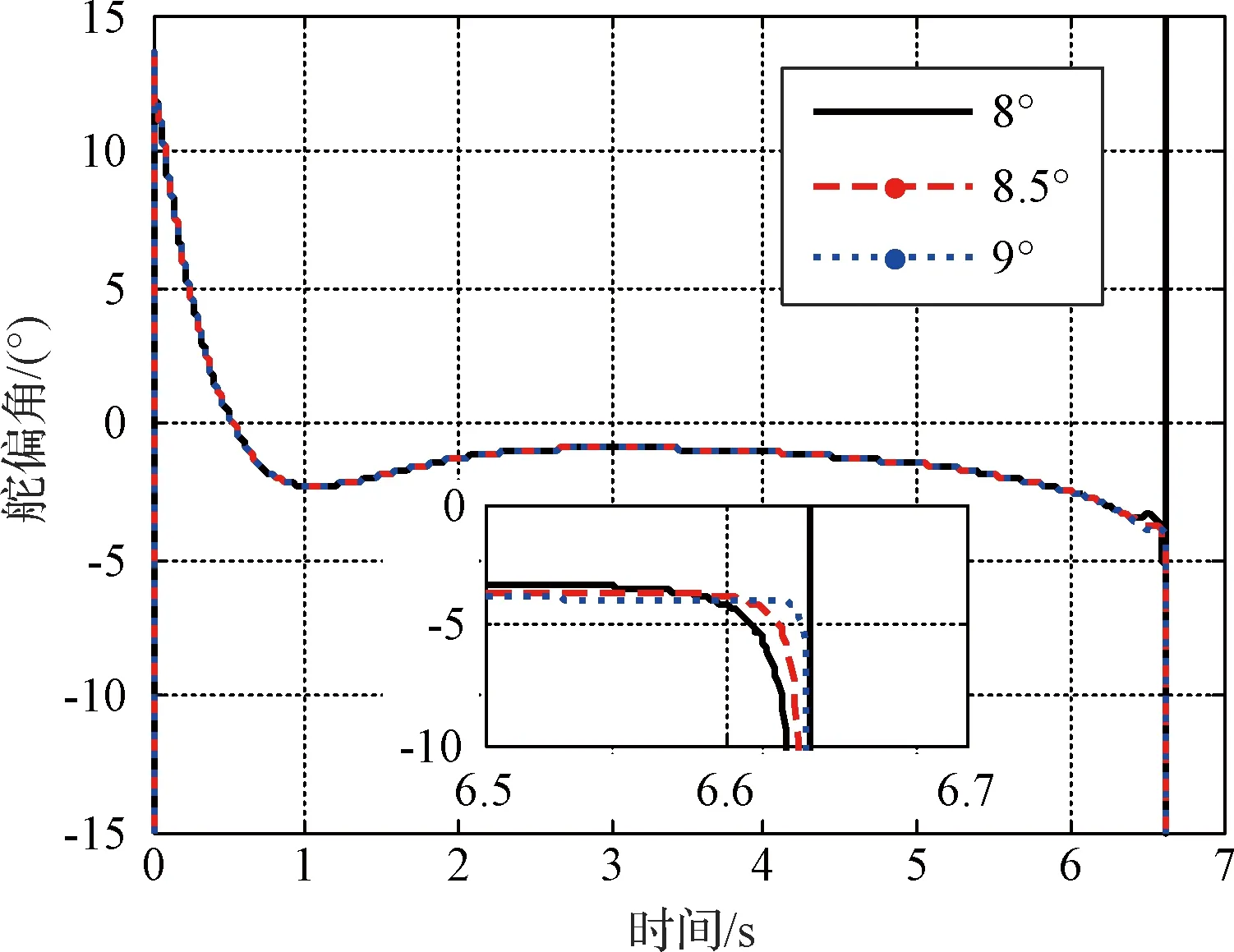
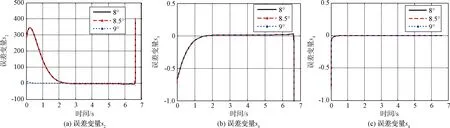
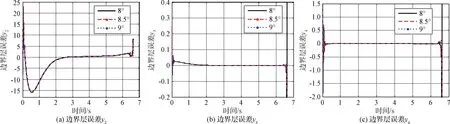
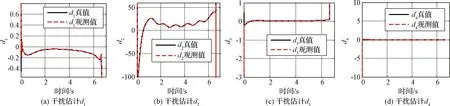
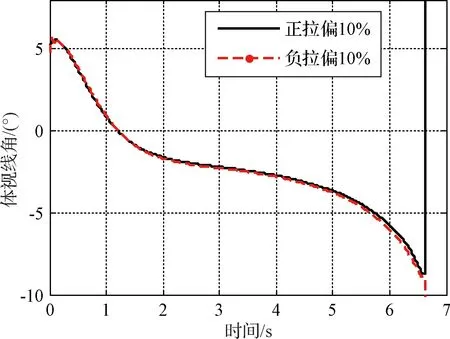

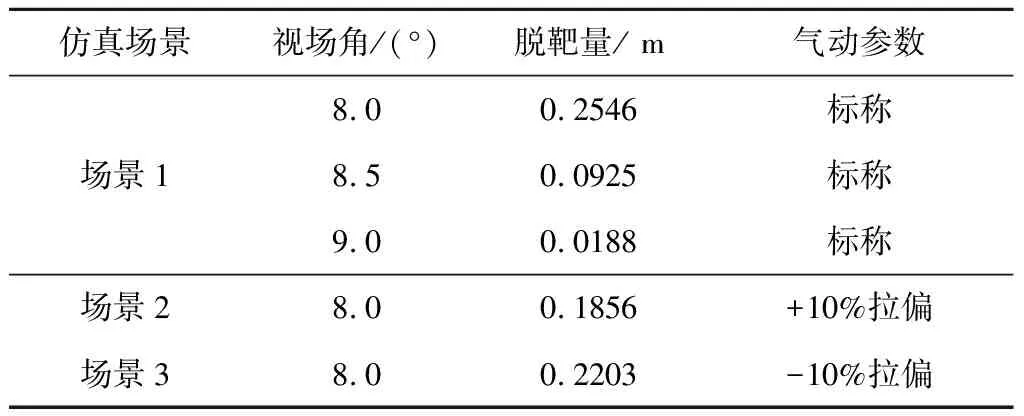
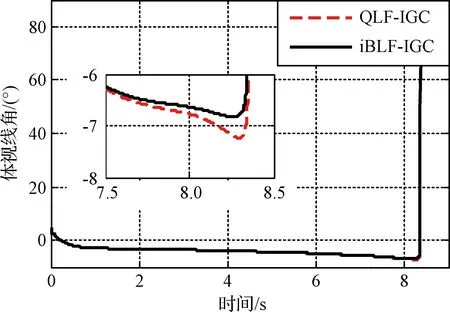
4 结 论

