差之毫厘，谬以千里

杨黎琴

摘 要：随着新课程改革的不断深入，小学数学教育发生了深刻的变化，教师的教学更加民主、灵活;学生的学习更加主动、创新，和谐的课堂氛围、民主的师生关系、多元的智能评价正在走向成熟。然而，新课程改革如黑夜前行，尽管方向明确，但还需我们去摸索。理所当然，这其中不乏困难、挫折、迷茫……本文试图就新课程背景下，小学数学常规教学中出现的教学细节进行反思，从而有效地提升教学效能。

关键词：细节教学 “书本”教材 “生本”教材 实践研究

在一定程度上，我们可以认为一节数学课就是由无数个细节共同组成的，精彩数学细节的设计是教师智慧与灵感的呈现。教学细节往往反映着教师的教学水平，折射着教师的教学思想，表达着教师的教学风格，体现出一位教师的实力和功力。“细节决定成败”同样适用于数学教学中，一些细小的教学细节，也决定着教学的成败。因此，为了教学的效率和质量，我们教师应在细节处下功夫，下面就来谈谈如何有效处理好数学细节教学中对“两本”教材的研究。

一、对于“书本”教材的研究。

一节好的数学课，首先要对教材进行准确把握，对教学方法进行灵活运用。在课堂上，教学是预设和生成的高度统一。其中，对“书本”教材的准确把握是至关重要的，可以说，教材把握不好，整个一节课就失去了灵魂。

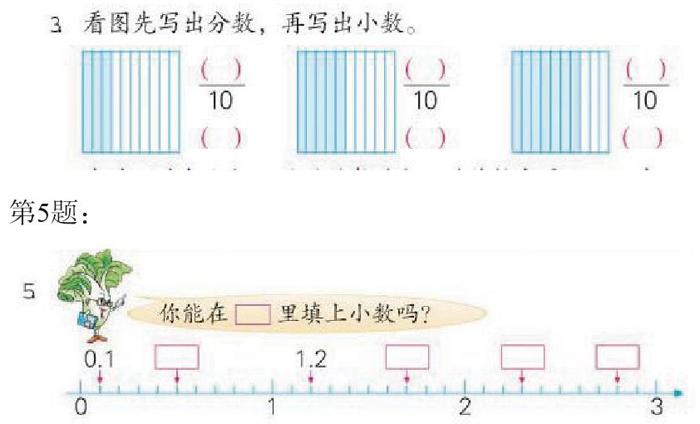
例如：在教学三年级（下册）《认识小数》时，有些教师由于没有认真钻研教材意图，对课后的“想想做做”也是蜻蜓点水，一带而过。对于第3题：

小数的认识在小学阶段通常分两段教学，这是由学生的年龄特征决定的。本阶段的认识小数，教材主要通过几个生活实例引入，让学生知道十分之几的数也可以用零点几的形式来表示，初步认识小数的意义。教学时，教师如果对这段教材的编排意图认识不到位，教学仅仅局限于几个具体的情境，这样对学生把握小数的意义是不利的。

事实上，从“想想做做”第3题和第5题的编排来看，编者已经很清楚地把这种意图呈现在我们眼前了：生活中，我们不仅可以把1米、1元平均分，只要是表示其中的十分之几，都可以用一位小数来表示。弄清教材的意图，就可以发现这两道习题对学生进一步认识小数的意义所起的“深化”作用。教师在备课过程中，也应紧紧围绕这个“深化点”展开教学设计。因此，备课时，我们必须认真分析与认识教材中的细节，只有深入细致地研究教学内容之间的联系，才能避免照本宣科的尴尬，才能使教学具有发展性。

平时在教学的过程中，我自认为教了很多年，对教材的理解很深刻了，闭上眼睛也能说出教材的重难点。可是在课堂教学中，尤其是练兵课、公开课上，自认为极其简单的内容，课堂上却是漏洞百出。究其原因，是平时在教学过程中对教材理解仅仅停留在表面，理解的比较肤浅，缺乏对教材进一步的挖掘与研究。我曾听过江阴市实验小学强震球老师的《角的度量》一课，他在这方面为我们做出了表率，课的大概流程是这样的：先比角引出单位角（100），再因测量不便，引出单位角合并。接着，精确测量引出工具细化。还有，读数不变，引出两圈刻度。最后进行技能训练。这样使学生对于度量角的方法掌握得相当透彻，可以说是环环相扣，一环紧扣一环，仿佛缺少不了其中的任何一个环节。

因此，教学的过程中，我们一定要注意对教材一些细节的处理，不要走形式过场，不要点到为止，要到合适为止。把教材处理到位，让学生不仅知其然还要知其所以然，让学生经历对知识的构建过程。让我们的教学不要因教不透或把握不准而遗憾。

二、对于“生本”教材的研究。

除了对“书本”教材的研究，还要对“生本”教材的研究，这里我所说的“生本”即学生本身。例如：一位老师在教学《认识千米》这一课时，教学重点是建立1千米的长度概念，掌握千米和米之间的进率。教学难点是千米概念的建立。对于三年级学生来说，1千米这一概念的建立难度较大。这堂课的关键是让学生参与对1千米的体验和感悟，联系学生的生活经验，并将生活经验转化为认知结构。课前布置学生走一走、拉一拉、跑一跑是非常重要的活动。如果没有这些活动，而只靠学生想象1千米有多长是无法建立1千米的观念的。

我也上过这节课，但仅限在电脑演示，学生是没有实际感受的。怎样让学生真切感受1千米的长度并形成1千米的长度观念呢？这位老师把“草地当桌椅，天空当教室”，孩子的思维异常活跃，让孩子在实质感知中建构了1千米=1000米。这堂课给孩子呈现的是“好玩”的数学。数学课上还要跑步？数学课上还要写作文？这些都是孩子们感到新奇和好玩的地方。在玩的过程中，学生在认识知识的同时感受和理解知识的真实意义，获得精神的丰富和心理的满足。这样的课堂，不仅挖掘“书本”细节，更关注“生本”细节，学生玩得痛快，学得扎实，而且也提升了数学效能。

再如教学《三角形的内角和》一课，数学的创造性思维能力是指学生在学习的过程中不拘泥于刻板的死套公式进行逻辑演算，而是在学习的过程中主动找出自己的问题，在反复的思考与实验中找到新的方法，总结出新的结论。

教学片段：

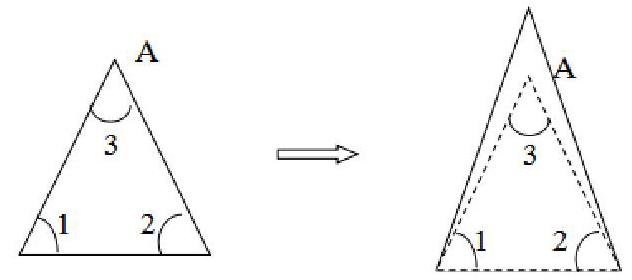
出示钉子板上的一个三角形。

学生尝试操作：

①拉动A点，使∠1、∠2变大。

②拉动A点，使∠1、∠2、∠3都变大。

生1：要使∠1、∠2变大容易，但是，要使∠1、∠2、∠3都变大，不可能做到。师：怎么回事呢？

生2：A点往下拉，∠3变大了，但∠1、∠2变小了。

生3：A点往上拉，∠1、∠2变大了，但∠3又变小了。

生：不可能都变大。

猜想：既然这样，猜猜看，三角形的内角和可能怎么样？

生：不变

师提问：①如果三角形内角和不变，有可能是多少度？（180°）

②你是怎么想到180°的？（三角板）

课件出示一副三角形板，说说三角板每个角的度数，并口算出它们的内角和。

引导：我们发现，三角板上的内角和确实是180°，但是，你们见过的三角形都长这样吗？（不是）那他们的内角和都是180°吗？需要验证。

本节课最关键的环节，在于验证“是否任何三角形的内角和都是180°？”根据学生的年龄特点，引导学生小组合作，动手验证。通过小组内交流，使学生认识到可以通过多种途径来验证，可以量一量、撕一撕、拼一拼、折一折、算一算……在明确验证方法后，学生在小组内通过动手操作、记录、观察，验证三角形的内角和是否为180°。就学生的发展而言，探究的过程比探究获得的結论更有价值。鼓励学生积极开动脑筋，从不同途径探究解决问题的方法，同时给予学生足够的时间和空间，不断让每个学生自己参与，在探索活动中，使学生学会与他人合作，同时也使学生学到了怎样由已知探索未知的思维方式与方法，培养他们主动探索的精神，让学生在活动中学习，在活动中发展。

总之，细节决定成败。关注细节，其实就是关注新课程的理念是否落实，新课程教学理念着陆课堂教学，课堂之美，其实就是细节之美，只有把握课堂教学中的关键性细节，才能使学生的数学思维获得扎扎实实的发展，提升课堂的有效教学。