编制高中数学变式题的思考

☉江苏省无锡市青山高级中学 李 赟

学生在从特殊到一般的推广、一题多解的变式、多题一解的变式中往往能够获得思维的拓展、视野的开拓及创新能力的提升，教师在变式教学这种“类”训练中应引导学生对一类数学问题的往复循环进行多角度的理解与认知并获得良好的预期.

一、“特殊”变式为“一般”

将数学原题中的特殊条件变为一般条件能令题目具备一般性或普遍性.

解析：设|PF1|=m，|PF2|=n.

在△PF1F2中，由勾股定理可得（2c）2=m2+n2=（m+n）2-2mn.

因为m+n=2a，所以4c2=4a2-2mn，即mn=2（a2-c2）=2b2.

又因为b2=9，所以S△PF1F2=1 2mn=b2=9.

观察原题，∠F1PF2=90°是一个特殊角，若∠F1PF2不是特殊角90°，而是60°或其他角度，此时勾股定理很难在其中运用，这又该如何计算？

变式1：若∠F1PF2=60°，则S△F1PF2=______.

解析：设|PF1|=m，|PF2|=n.

由此可见，虽然改变了原题的角度，但是根据椭圆的定义与余弦定理也是可以得出结果的，那么改成其他一般性条件，是否可以得到一般性结论？具备推广的意义吗？

如此变式对学生数学思维的锻炼是极有意义的，学生在从特殊到一般的推广中往往能够获得数学学习的愉悦和成就感.不仅如此，一题扩充至多题的训练也令学生对题型的归纳总结有了新的感悟，这是盲目的题海训练所无法比拟的，这样的课堂教学对于学生来说也更具新鲜感与乐趣.

二、一题多解的变式

利用不同的数学原理、方法与思路对同一数学问题进行思考和解题即为我们通常所说的一题多解.

例2 在△ABC中，点D在BC边上，且DC=2BD，AB∶AD ∶AC=3∶k∶1，则实数k的取值范围为______.

解法1：（向量法）设AB=3t，AD=kt，AC=t（t＞0），则：

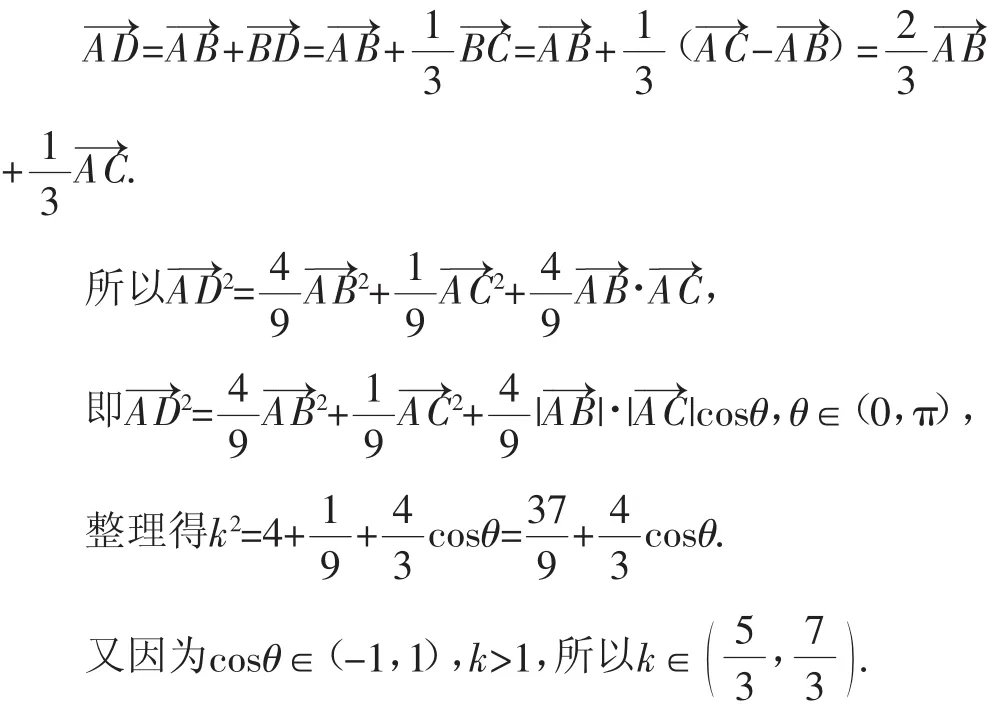
从向量的角度出发并将题中条件用向量表示出来，将所求向量用基向量表示并运用数量积最终令问题得解，这种解题方法是解决这类问题的一种常用方法，数学化归思想在这一解法中得到了很好的体现.

这是根据阿波罗尼斯圆满足的条件进行联想所得到的一种解法，学生在教师的点拨下很快联想到动点A的轨迹为圆并运用坐标法来解题.

解法3：（解三角形） 设AB=3t，AC=t，AD=kt，BD=m，DC=2m（t＞0，m＞0）.

这是观察三角形并发现边角之间关系所得的一种解法，事实上，也可以根据AB+AC＞BC，AB-AC＜BC得出，由此可以进一步引导学生，令其观察三角形三边关系并最终获得解法4.

解法4：（几何法）设AB=3t，AC=t，AD=kt，BD=m，DC=2m，过点C作CE∥AB，延长AD交CE于点E，则△ABD∽△ECD，所以有

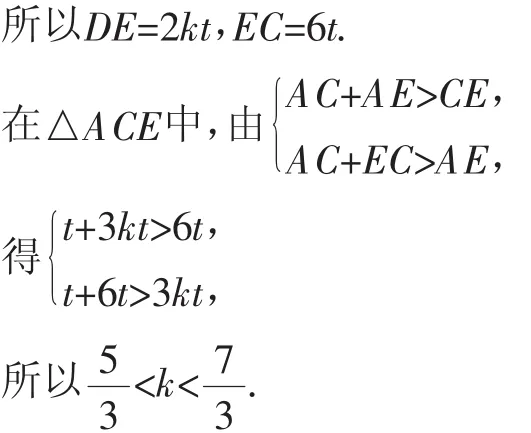
由此可见，很多问题往往存在能够体现不同思维角度的多样化解法.

由此不难看出，重视例题的变式或引申能使数学问题的内涵与外延得到积极的探索，课堂教学内容由此得以丰富，学生知识体系的形成与建立也在更加高效的课堂教学中得以顺利实现.

遵循一定的原则与要求将原题中的条件、结论、形式、内容、图形进行适当的改变并提出新问题就是变式.教师在变式教学这种“类”训练中应引导学生对一类数学问题的往复循环进行多角度的理解与认知，使学生在感受数学无穷变化的奥妙中不断提升学习效率，在开拓视野与提升创新能力的同时顺利获得良好的学习预期.F