最值诚可贵，探究价更高——对一道数量积最值问题的探究

☉江苏省口岸中学 孙 娟

平面向量的数量积问题一直是高考题及各类模拟题中的常见题型与热门考点之一，其往往涉及平面向量的数量积的求解、最值的确定、参数的求值等问题，且难度中等偏大.从哪些常见的角度切入及如何正确地破解，是处理此类问题的重点所在.

一、问题呈现

例题 已知矩形ABCD的边长AB=2，AD=4，点P，Q分别在边BC，CD上，且∠PAQ=的最小值为________.

本题以矩形为问题背景，结合矩形相关边上已知两点及相应的角度问题，进而来求解对应的平面向量的数量积的最小值.其中巧妙结合了平面几何图形、三角函数、平面向量及函数的最值等，融合了动与静、变与不变、常数与最值等对立统一体，能够很好地培养素养，并考查能力.

二、多解探究

解决平面向量的数量积的相关问题时，经常采用坐标法思维，通过建立平面直角坐标系，把问题转化为坐标运算的问题来处理，再结合相关参数所对应的基本不等式的转化，一般来说可以简化推理步骤，优化运算过程，提高解题效益.

解法1：以A为坐标原点，AD，AB所在的直线分别为x轴，y轴建立平面直角坐标系.

设P（m，2），Q（4，n），其中0≤m≤4，0≤n≤2，则0≤mn≤8.

解决涉及平面几何中平面向量的数量积问题时，可以引入对应的角度，利用三角函数的相关知识加以转化，结合平面向量的数量积公式，再结合三角恒等变换，以及三角函数的图像与性质来确定相应的最值问题.

三、变式拓展

其实，通过对平面向量的数量积最值问题的求解并深入观察，根据条件加以拓展，可以进行深化与变式，从中发现问题，提出问题，分析问题，并得以解决问题，真正达到“解一题拓一类，拓一类通一片”，避免“题海战术”，从而真正培养思维品质，提升解题思维与解题能力，以不变应万变.

探究1：通过改变题目中相应角的度数来达到变式的目的，可得以下变式.

变式1：已知矩形ABCD的边长AB=2，AD=4，点P，Q分别在边BC，CD上，且∠PAQ=的最小值为________.

故填答案：16 2 -16.

探究2：通过改变题目中相应角的条件，将其变为对应线段的长度来达到变式的目的，可得以下变式.

变式2：已知矩形ABCD的边长AB=2，AD=4，点P，Q分别在边BC，CD上，且PQ=2，则的最大值为________.

解析：以A为坐标原点，AD，AB所在的直线分别为x轴，y轴建立平面直角坐标系.

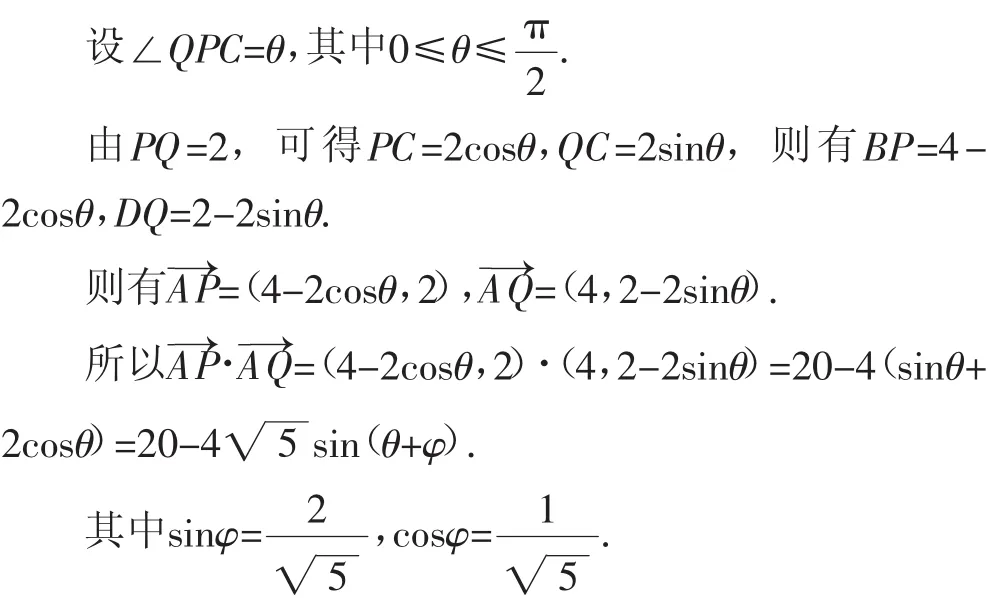
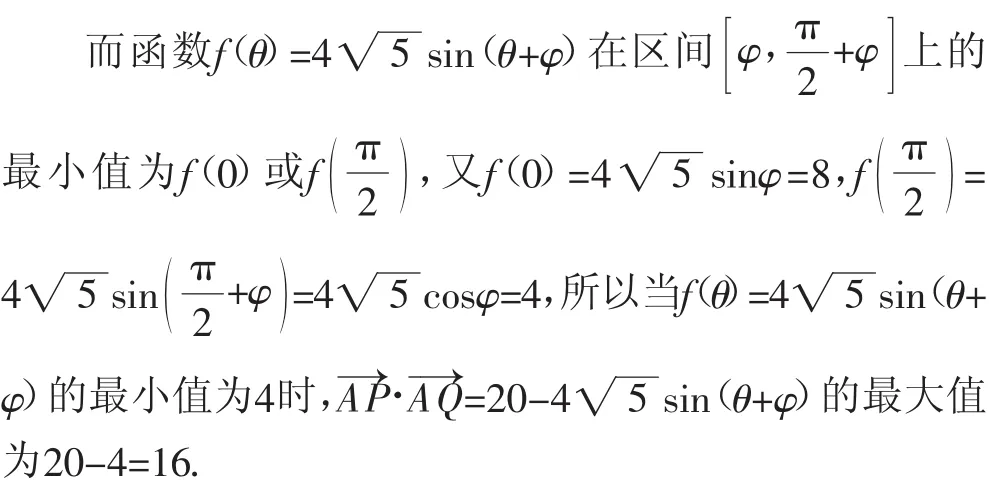
故填答案：16.

变式3：已知矩形ABCD的边长AB=2，AD=4，点P，Q分别在边BC，CD上，且PQ=2，则的取值范围为________.

解析：以A为坐标原点，AD，AB所在的直线分别为x轴，y轴建立平面直角坐标系.

通过从多个不同角度来探究处理，巧妙地把该题的底蕴充分挖掘出来.从多角度出发，多方面求解，进而深层次拓展，真正体现对数学知识的融会贯通，充分展现知识的交汇与综合，达到提升能力，拓展应用的目的.进而真正达到在学中“悟”，在“悟”中不断提升解题技能.正如我国著名数学家苏步青先生所说：“学习数学要多做习题，边做边思索，先知其然，然后知其所以然.”F