基于改进粒子群模糊神经网络的信用评估
熊志斌
(华南师范大学 数学科学学院,广州 510631)
0 引言
由于信用风险度量的复杂性与非结构性,使得传统的统计计量模型在风险评估中的效果往往不尽人意。近年来,神经网络以其灵活的学习能力和优良的非线性建模等特性而受到研究人员的高度重视,并在信用评估领域中得到了广泛运用[1]。然而神经网络存在“黑箱操作”、结果解释性差等缺陷而让人诟病。随着研究的不断深入,有研究者开始将具有逻辑推理功能,擅长处理不确定性、不精确信息的模糊逻辑与神经网络相结合起来,来改善上述缺陷,并在风险管理研究的实践中取得了较好的效果[2,3]。不过上述模型中优化模型参数的方法为BP算法或是基于梯度下降的寻优算法,这种模型并未解决一般神经网络所存在的学习速度缓慢、易陷入局部最优等缺陷。而以粒子群算法为代表的群智能优化算法是用搜索空间中的点模拟自然生物中的个体,将生物的优胜劣汰过程或觅食过程类比为可行解变换优化的迭代过程,该算法相比BP等梯度算法而言具有全局性能良好、操作简单且易于实现的优点[4]。然而,粒子群算法也存在着不能兼顾收敛速度、全局探索能力和局部精细搜索能力的问题,在迭代后期易出现“早熟”现象[5],针对上述缺陷,一个改进思路就是综合不同算法技术,使得不同方法技术之间相互补充、相互促进,最终达到改善优化算法的性能,提高模型预测效果的目的。
基于此,本文提出一种改进的粒子群算法——混沌小生境粒子群算法,来改善上述缺陷。首先基于混沌运动的遍历性特点,在算法初始化时采用混沌迭代产生粒子的初始位置和速度以提高种群的多样性;然后借鉴遗传算法中的常用的小生境技术来改进粒子群算法在进化过程中的多样性,提高算法的全局寻优性能和收敛速度。通过这种改进算法对模型参数进行优化,构建了混沌小生境粒子群模糊神经网络模型,并运用该模型对我国上市公司信用风险状况进行评估预测。
1 模糊神经网络结构
本文所采用的模型为四层网络模型结构,具体结构如图1所示,其中n为输入维数,m为模糊子集的个数,wj是模糊推理层第j个节点到输出层节点的耦合权值。这里用分别表示第l层第i个节点的输入和输出。

图1网络模型结构
每层的输入和输出具体表达如下:
(1)第一层(输入层):这一层有n个节点,这些节点仅仅将输入值传递到第二层。

(2)第二层(模糊化层):这一层共有mn个节点,共有n组。每个节点与输入变量的一个语言变量标识相对应,隶属值确定了输入变量的模糊集程度。本文采用Gaussian隶属函数。
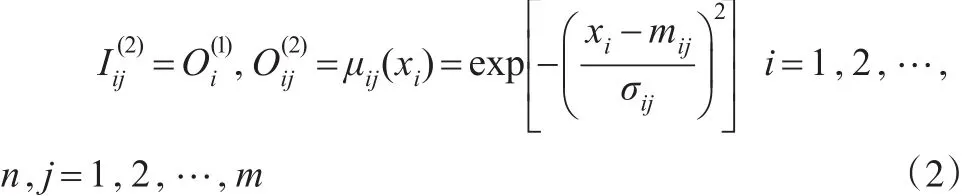
其中 μij(xi)是模糊变量隶属函数,mij,σij分别为Gaussian函数μij的中心和宽度。
(3)第三层(模糊推理层):该层共有m个节点,其输入输出表达式为:

(4)第四层(去模糊化层):1个节点,该节点计算前一层输出之和并将其作为总输出。

其中wj是第三层第j个节点到第四层节点的耦合权值。
2 混沌小生境粒子群优化算法
2.1 标准粒子群算法
在标准的PSO算法中,其解的好坏是由适应度函数值来评价,适应度函数的设计与目标函数有关,要根据实际研究问题来确定。种群中的每个粒子都代表一个可能解,它包括粒子自身所处位置及速度,粒子速度决定了其搜索的更新方向和距离。粒子在搜索过程中,是通过跟踪个体最优位置(即个体极值pbest)和全局最优位置(即全局极值gbest)来更新自身的。在标准PSO算法中,粒子的位置和速度根据如下方程进行更新[4]:
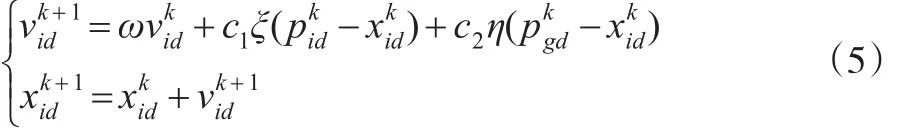
2.2 混沌小生境粒子群算法
一般来讲,由确定性方程得到的具有随机性的运动状态都可称为混沌,其中Logistic映射就是一个典型的混沌系统[7],其迭代公式如下:

其中,k=1,2,3,…,α为控制参数,α∈(2,4]。在这里,本文主要是利用混沌运动的遍历性,即通过混沌迭代产生大量的初始群体,从中选出较好的初始群体。
小生境技术是通过强迫个体分布在不同“生境”的方法,增加个体多样性,避免算法陷入局部极值无法跳出。本文将基于限制竞争选择策略(Restricted Competition Selection,RCS)的小生境技术与粒子群算法结合起来,构建小生境粒子群算法(niche evolution PSO,NEPSO)来改进算法的搜索精度和寻优性能。RCS策略的主要优点是能够将小生境范围内的两个解中较差的淘汰掉,保证种群朝最优解方向运动;另外,RCS策略是以种群最优位置之间的距离作为小生境之间的距离,当两个生境距离小于某一设定的阈值时,较好的生境予以保留,而对于较差的种群进行重置,即将种群内最优个体作为种群的最优极值,并重新初始化种群内的其他被选中粒子。这样既保证了搜索朝着最优方向进行,又使得每个小生境种群间的搜索是相互独立的,保证了多样性,而且当生境发生相互干扰时,该策略仅需对极少数几个最优个体粒子进行控制,极大减少了算法复杂度,提高了算法效率。RCS策略更详细的介绍可参看文献[8],这里不再赘述。
这里,本文引入RCS小生境技术来改进粒子群算法的寻优性能,通过以下粒子状态更新方程来对粒子状态进行更新,既防止不同种群趋同,又保证种群的多样性,粒子状态更新方程如式(7):
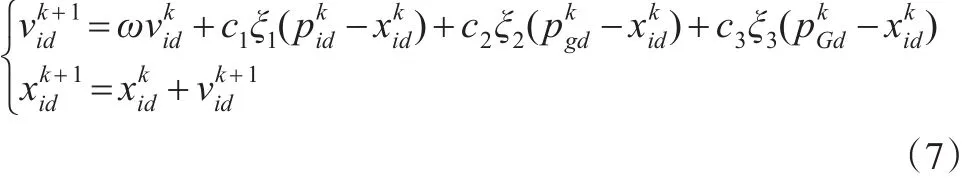
混沌小生境粒子群算法(CNEPSO)的具体步骤如下:
步骤1:产生初始种群和若干小生境子种群;初始化算法参数,包括惯性权重ω,随机数ξ1、ξ2和ξ3,学习因子c1、c2和c3等;
步骤2:进行混沌初始化。对每个种群都随机产生一个n维的每个分量数值都在0和1之间的向量yo=(y01,y02,…,yon),yi(i=1,2,…,N)由式(6)给出,其中N为种群规模;然后再根据式子 xij=xmin+yij(xmax-xmin),(i=1,2,…,N;j=1,2,…,n)计算粒子的位置,通过计算目标函数,从N个初始群体中找出较好的m个解作为初始位置,随机产生m个初始速度;
步骤3:对所选出的粒子,根据当前位置和速度产生出新的位置;
步骤4:对每个子种群中的每个粒子评价其当前的适应值。这里使用误差平方和(SSE)的倒数作为评价函数,即,以自身当前位置作为每个粒子的个体极值,以每个子种群中的最优粒子作为子种群的最优极值,所有粒子中最优粒子则被视为整个种群中的全局最优极值
步骤5:执行RCS小生境技术策略,确定每个小生境子种群中的最佳个体粒子,每个子种群中的最佳粒子被选中重新组成一个新的种群Newgroup;
步骤6:对每个子种群内(不含Newgroup)的个体按式(7)进行更新(包括位置和速度);
步骤8:每个种群按小生境技术操作,不断迭代,当迭代一定次数时,对最差的子种群重新初始化;
步骤9:当迭代一定次数后,计算种群Newgroup内所有粒子适应度值,并按标准PSO的粒子更新方程式(5)更新粒子位置和速度;
步骤10:检查是否满足算法终止条件。本文使用两条学习终止准则:1)误差平方和MSE;2)最大进化代数M。若MSE<ε(这里ε为事先设定好的值)或M达到预先设定的迭代次数,则中止算法并输出结果;否则,令k=k+1,转到步骤6直到终止条件满足。
3 信用评估建模实例
3.1 样本来源与数据预处理
本文以我国上市公司中ST公司(包括*ST公司)和非ST公司作为研究对象,根据唐振鹏等(2016)的观点[9],虽然ST、非ST公司与公司信用好坏并不完全等同,但它们之间有着很强的相关性,在上市公司信用研究中可以把ST公司视为信用差(危机)公司,非ST公司视为信用好(正常)公司,本文采用了这种观点。本文样本数据来源于Wind数据库和同花顺财经数据库,由于公司t年被宣布ST处理和该公司公布t-1年度财务报表几乎是同时发生的,故本文采用t-2年的财务数据来预测t年是否会被ST,例如2014年被宣布ST的公司,则采用2012年财务数据来进行分析。本文在借鉴国内外有关文献的基础上,并结合指标的可比性、同趋势性原则,选取了10个指标,即:资产净利率(X1),主营业务利润率(X2),净资产利润率(X3),资产负债率(X4),速动比率(X5),已获利息倍数(X6),经营现金总债务比(X7),总资产周转率(X8),应收账款周转率(X9),主营业务收入增长率(X10)。
对于原始指标数据,本文进行了归一化处理,归一化函数如式(8)所示:

这里,X代表输入矩阵,max x和min x分别为X中的最大和最小值。由此可知,该网络模型的输入层节点为10,模糊子集数设为3,网络模糊化层节点数则为30,去模糊化层节点数设为3,输出变量为单变量y,即输出层为一个节点,若y=1则代表信用差(ST公司),y=0则代表信用好(非ST公司)。因此,该模型的结构为一个10-30-3-1网络结构。
3.2 交叉验证与模型参数选取
为了尽量减少随机划分训练样本集和测试样本集所可能带来的偏差,同时也为了提高模型的泛化能力,更有效地检验模型的准确性和可靠性,本文采用n重交叉验证(n-fold cross-validation)方法来评估模型对信用风险分类的有效性。具体方法为:初始样本集合(300家公司)被划分成5组互不相交的子集,每组样本数都为60家(14家ST和46家非ST公司)。每一次模型在除了一个子集之外的其他子集上进行训练,而未被训练的子集则用来作为测试集。整个过程被重复5次试验,每次使用一个不同的子集进行验证,所构建模型总的分类准确度是通过这5次试验中所得到的分类准确度加总后的简单平均值求得。
在本文中,种群大小被设定为60,初始子种群数为3,ξ1、ξ2和ξ3为[0,1]区间内均匀分布的随机数;惯性权重ω取值区间为[0.4,0.9];学习因子 c1=1.5,c2=0.2,c3=0.5;xmin=-10,xmax=10;vmax=8;样本学习中止条件:①MSE<0.001;②最大迭代数为5000。
3.3 实证结果
本文通过5重交叉验证的方法来验证所构建的混沌小生境粒子群模糊神经网络(CNEPSO-FNN)的有效性,具体结果见表1。
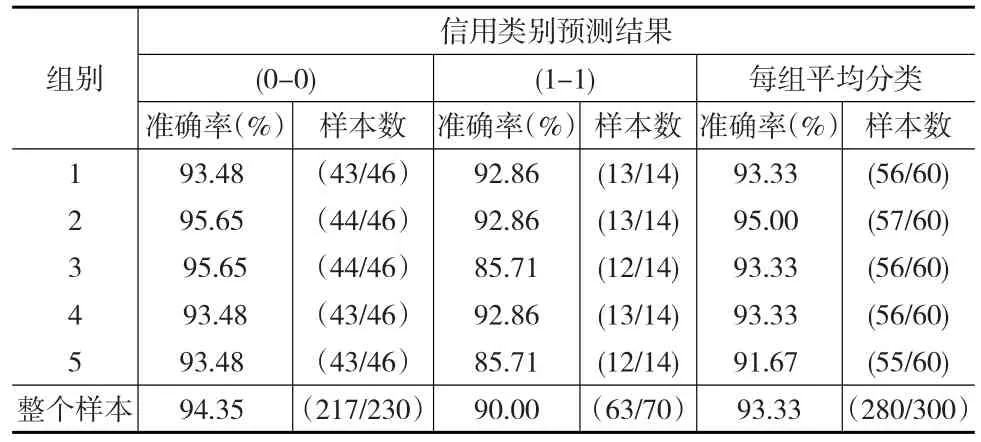
表1 CNEPSO-FNN模型交叉验证结果
表1中,0代表信用好的公司,1代表信用差的公司。0-0表示正确区分出信用好的公司的准确率或样本数,1-1表示正确区分出信用差的公司的准确率或样本数。从表1可看出,模型对5组平均分类准确率分别达到93.33%、95.00%、93.33%、93.33%和91.67%,对整个样本的平均分类准确率达到了93.33%,效果相当不错。
作为对比,本文在构建CNEPSO-FNN模型同时,还另外分别构建BPNN和SPSO-FNN(采用标准PSO算法优化模糊神经网络)两种模型。表2给出了这三种模型对总体样本预测准确率的对比结果。
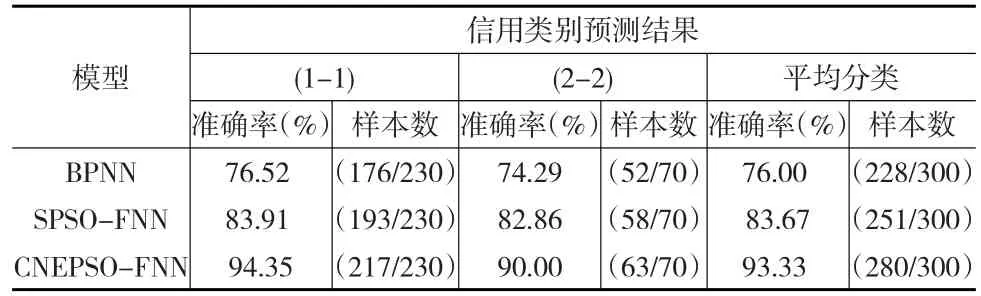
表2 三种模型的测试对比结果
与表1一样,表2中0-0表示正确区分出信用好的公司的准确率或样本数,1-1表示正确区分出信用差的公司的准确率或样本数。正如表2所示,BPNN和SPSO-FNN模型在300个样本中预测正确的样本数分别为228和251,预测准确率分别为76.00%和83.67%,而CNEPSO-FNN模型预测准确的样本数为280个,准确率达到了93.33%,远高于前两个模型,也说明构建的CNEPSO-FNN模型的有效性和可靠性。
4 结论
本文提出了一种改进的粒子群算法,即将混沌技术、小生境技术与粒子群算法结合构建了混沌小生境进化粒子群优化算法。首先利用混沌遍历性特点,采用混沌迭代初始化粒子的位置和速度,接着在一般小生境技术的基础上,为了避免小生境的相互重叠,采取了淘汰策略对距离太近的小生境进行淘汰,通过淘汰策略使得过于接近以至重叠的小生境重新分化与组合,以便各个小生境保持独立的搜索空间。通过这种改进,改善了种群的多样性,提高了算法的全局寻优能力。将这种改进的粒子群算法与模糊神经网络模型相融合,构建了改进的粒子群模糊神经网络——混沌小生境粒子群模糊神经网络,并利用中国上市公司数据,进行了信用评估预测,实证检验结果也表明了该评估模型的有效性和可靠性,该研究成果也为探索符合我国实际的信用评估技术方法提供了一些参考和借鉴。

