一类不可观测变量模型的特征研究

徐成波

（四川旅游学院 经济管理学院，成都 610100）

0 引言

Gertler和Waldman（1992）[1]在考虑无法观测到的质量变量时，提出了模型估计的方法，这一关键技术解决了长期以来实证研究中无法获得不可观测的质量数据的难题，在实证分析中产生了较大影响。Mocan（1995）[2]的模型在此基础上有所变化，不仅省略了其中的许多项，而且还加入了虚拟变量。但二者的关键点都是采用了质量调整成本函数，分析护理行业提高相应的质量水平测度成本会增加多少。

质量调整成本函数的逻辑起点为古典经济学的成本函数，但该函数并没有考虑质量因素（包括食品安全和产品质量），即质量因素是外生的。后来，Braeutigam和Pauly（1986）[3]作出了开创性的贡献，将质量纳入成本函数，并检验出质量变量是内生的，指出在此情况下如果没有考虑质量将导致有偏估计。但该文献没有提供此时如何估计成本函数的方法。Gertler和Waldman（1992）[1]在此基础上又进一步做出了上文所提到的贡献。而Antle（2000）[4]将此方法引入到对食品安全生产方面的研究中，对食品安全作了类似的处理，准确测度出食品安全生产所产生的成本，从而为食品安全监管政策的制定及评估提供科学的解释。国内学者王志刚等（2012）[5]首次采用了Antle（2000）[4]的方法，通过对全国334家实施HACCP的食品加工企业进行实证研究。

从国内外的研究来看，质量调整成本函数在该类研究中得到了广泛应用，在解决无法观测到的产品质量和食品安全变量时，具有很强大的功能。但质量调整成本函数设定形式的科学性和复杂的数学特征还有待研究，这将有助于更灵活地使用该类函数。

1 模型构建

在此借用Gertler和Waldman（1992）[1]、Antle（2000）[4]的分析框架，引入质量调整成本函数C=C（Y,S,Q,W,K）和导出的均衡食品安全方程S=S（Q,W,K,P,Z），其中，C是总成本，Y是总产量，S是食品安全，Q是产品质量，W是要素价格，K是资本，P是产品价格，Z是刻画市场需求状况的变量，包括经济和人口特征等。从目前国内外的研究来看，各种文献对质量调整成本函数均采取了超越对数成本函数形式，该函数是经验研究中最频繁使用的灵活函数形式，在众多奇异的函数形式中成为最可靠与最受欢迎的函数。其特征为包含每个解释变量的一次项、二次项和变量之间的交互项①将式（1）设定为超越对数成本函数形式时，对于变量S而言，还存在一些项lnSlnY、lnSlnK、lnSlnW、lnSlnQ；因lnSlnY与变量Y构成的lnYlnS相等，故任选择一项即可。其他变量的构造也作类似处理。：

其中，h=1,⋅⋅⋅,H种生产要素，υ为随机扰动项，α为涉及食品安全变量S的所有项，等于αyslnYlnS+1/2ηss（lnS）2。由式（1）可导出第h种要素的成本份额方程：

在实证分析中，由式（1）超越对数成本方程和式（2）要素成本份额方程组成系统结构模型，将均衡食品安全方程带入其中，转化为系统简化模型，采用似不相关估计（简记SUR），以提高估计的效率，最终通过系统简化模型的参数求解系统结构模型的参数。

如果上述系统结构模型简记为Y=Xβ+ε，那么运用SUR的参数估计量可表达为[6]：

其中，Ω为扰动项ε的方差-协方差矩阵。在式（3）中存在的前提条件是Ω为非奇异矩阵。这意味着，如果Ω为奇异矩阵，那么就难以运用SUR来估计系统结构模型，这是此类实证分析需要着重解决的一个重要问题。

2 模型特征分析

2.1 超越对数成本方程为二阶泰勒展开式

为说明式（1）设置的科学性，提出以下命题：

命题1：超越对数成本方程为质量调整成本函数的二阶泰勒近似。

证明：假定一元函数y=f（x）在领域内连续、可微，并且n阶导数存在。则y=f（x）在点x0处的泰勒展开式为：

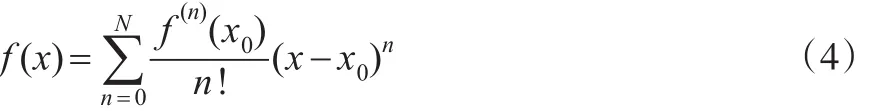
多元函数的泰勒展开形式与一元函数类似，只是由于前者向量乘积表达式的复杂性，造成了二者表达形式上的差异。

将上文式（1）记为：

对式（5）中解释变量X赋初始值，即分别为lnY0,lnK0,lnW0,lnQ0,lnS0。根据上述式（4）泰勒展开式的形式，式（5）二阶以下的泰勒展开式各项分别为：零次项lnC0=C（lnY0,lnK0,lnW0,lnQ0,lnS0），一 次 项 g（lnX0）T（lnX-lnX0），二 次 项（lnX-lnX0）TH（lnX0）（lnX-lnX0）。其中，一次项中的 g（lnX0）为梯度形式，可表达为：

二次项中的H（lnX0）为海塞矩阵形式，可表达为：

一次项和二次项中的lnX-lnX0可表达为[lnY-lnY0,lnK-lnK0,lnW-lnW0,lnQ-lnQ0,lnS-lnS0]T

于是式（5）的二阶泰勒近似可表达为：

令g0≡g（lnX0）、H0≡H（lnX0），则式（8）可整理为：

结合式（5）中的lnX和式（7）H0的形式可以知道，式（9）中 （lnX）TH0⋅lnX0和 （lnX0）TH0⋅lnX展开为一系列标量的乘积，而多个标量的乘积可交换相应的位置，故（lnX）TH0⋅lnX0=（lnX0）TH0⋅lnX；如果式（5）二阶偏导连续可微，根据杨氏定理（Young "s Theorem），那么，式（7）海塞矩阵H为对称方阵，即H0=HT0。进一步可以得到：（lnX）TH0⋅lnX0=（H0⋅lnX0）T⋅lnX。这样，式（9）可变为：

将式（5）省略了的三阶以上泰勒展开式各项统一纳入扰动项u中，那么式（10）可精确地表达为：

将式（5）lnC0、式（6）g0和式（7）H0带入式（12）进行展开，通过一系列较为繁琐的计算整理，便可得到上文式（1）超越对数成本方程。限于篇幅原因，在此省略这一过程。

综合上述分析可知，超越对数成本方程为在各解释变量初始值lnY0、lnK0、lnW0、lnQ0和lnS0的二阶泰勒近似。从式（12）还可以看出，上文式（1）超越对数成本方程各系数为解释变量初始值、关于解释变量初始值的梯度和关于解释变量初始值的海塞矩阵的线性组合。

证毕。

2.2 超越对数成本方程相关参数约束条件

命题2：超越对数成本方程参数满足以下条件

证明：为简化分析，暂时省略上文式（1）超越对数成本方程的食品安全变量S，即省略α，相应地，式（2）要素成本份额方程也就不存在lnS一项，这并不影响整个推导过程①如果不省略食品安全变量S，那么在将均衡食品安全方程带入式（1）超越对数成本方程时，只会增加繁琐的计算过程。在合并整理以后，整个推导过程与省略食品安全变量S的情况完全类似。。将式（2）按h种要素展开：

将式（5）按 h种要素记为C（lnY,lnS,lnQ,lnW1,lnW2,…,lnWH,lnK）=lnC，假定h种要素的价格均增加λ倍，由上文式（5）可得：

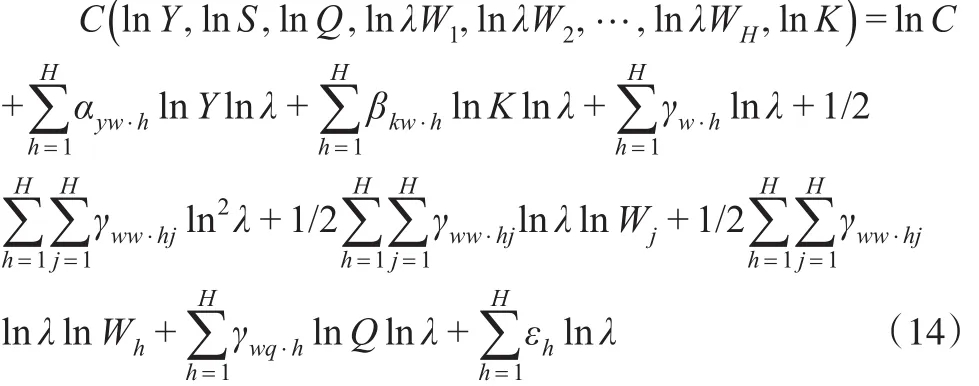
在式（14）中，结合式（13）所隐含的约束条件，可得出：

如果式（1）是关于各种要素价格的一次齐次函数，那么由式（5）可得：

式（15）和式（16）为完全不同的两个式子，由此可知，命题2的约束条件是由和对称条件γww⋅hj=γww⋅jh推导出来的，而并不涉及超越对数成本方程是否为一次齐次函数②Gertler and Waldman（1992）、Antle（2000）认为参数约束是由对称矩阵假定和超越对数成本方程为各种要素价格的一次齐次函数两个条件推导得出，这是不正确的。。

证毕。

2.3 系统结构模型扰动项方差-协方差矩阵为奇异矩阵

命题3：超越对数成本方程和要素成本份额方程组成的系统结构模型扰动项方差-协方差矩阵为奇异矩阵。

证明：假定上文式（2）H个要素成本份额方程组成系统模型，而系统模型的扰动项为ε，即ε=[ε1ε2…εH]T，则那么：

从式（18）可以看出，Ω为非奇异矩阵是保证上文式（3）SUR参数估计量存在的必要条件。假定上文式（2）的扰动项依然具有零均值的特性，即Eε=0；那么由式（17）可得：

其中，⊗为克罗内克尔乘积（Kronecker product），Σ⊗IH表示矩阵Σ每一个元素与IH相乘。根据行列式性质，将式（19）Σ的行列式的第1行至第H-1行加到第H行，结果为：

推论1：在H个要素成本份额方程组成的系统模型中，加入超越对数成本方程，依然没有改变系统结构模型扰动项方差-协方差矩阵的奇异性。

推论1的证明与命题3的证明类似，限于篇幅，省去证明过程。命题3意味着超越对数成本方程和要素成本份额方程组成的系统结构模型不能用SUR进行估计，因为在此系统结构模型框架下，式（3）并不成立，这是在实证分析中极易犯的一个严重错误。为解决这一问题，提出以下推论：

推论2：在H个要素成本份额方程和超越对数成本方程组成的系统结构模型中，“任意”去掉一个成本份额方程将改变系统结构模型扰动项方差-协方差矩阵的奇异性。

推论2的证明与命题3的证明类似，限于篇幅，省去证明过程。

2.4 系统结构模型扰动项方差-协方差矩阵奇异性处理过程

延续推论2，为解决系统结构模型扰动项方差-协方差矩阵奇异性问题，提出以下命题：

命题4：“任意”去掉一个成本份额方程指在系统结构模型中，超越对数成本方程的被解释变量和要素价格解释变量同除以被剔除的成本份额方程所对应的要素价格；剩下的H-1个要素成本份额方程的要素价格解释变量也同除以被剔除的成本份额方程所对应的要素价格。

证明：与命题2的证明类似，为简化分析，也省略上文式（1）中的食品安全变量S。

如同推论2的证明，不失一般性，假定“任意”去掉一个要素成本份额方程，比如SH。那么，由命题2的约束条件可得：

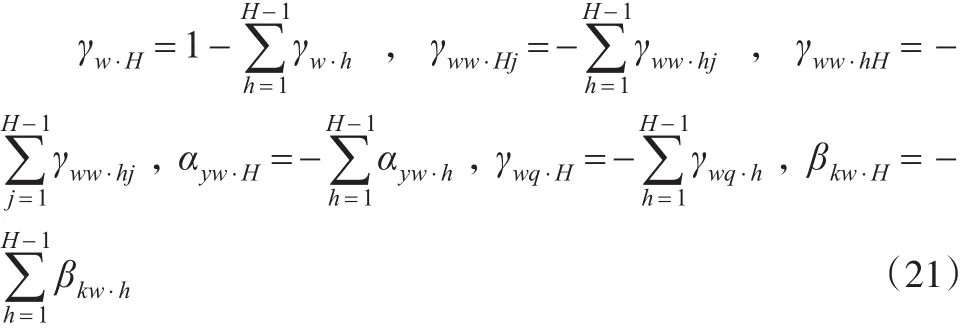
将式（21）的约束条件分别带入上文中式（1）和式（2）H-1个要素成本份额方程，并经过较为繁琐的整理后，得到：

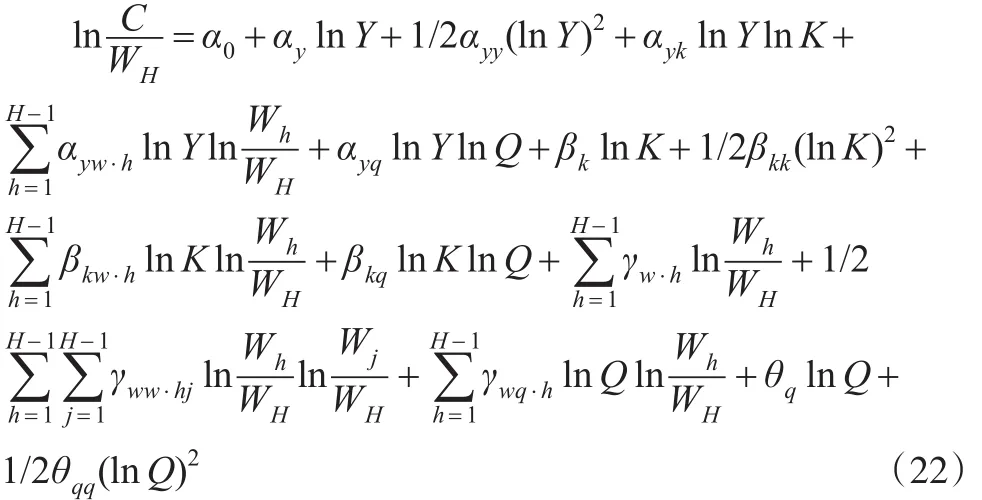
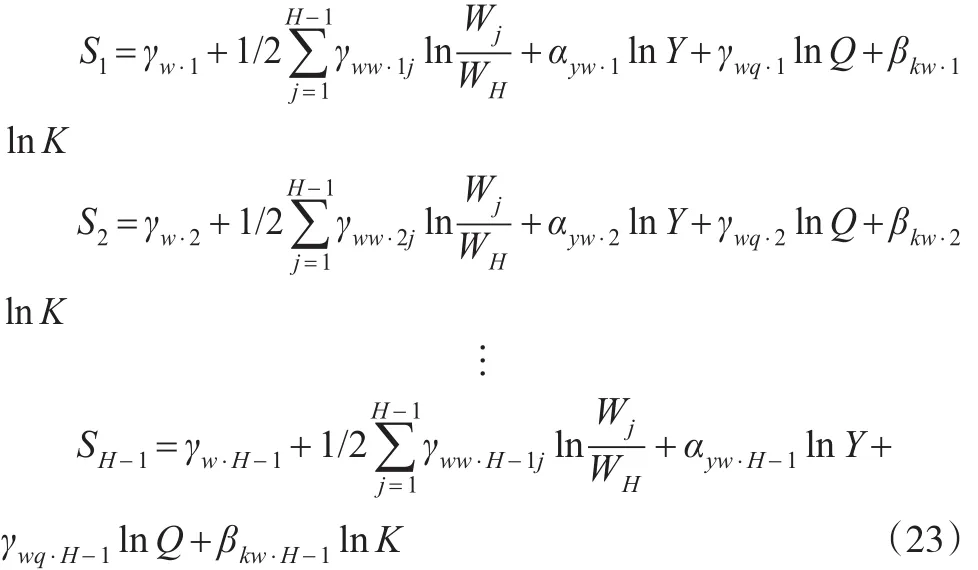
式（22）和式（23）为系统结构模型去掉要素成本份额方程SH的表现形式。事实上，在式（23）中，通过估计H-1个要素成本份额方程，然后根据式（21）的约束条件，即可求出第H个要素成本份额方程的参数，从而得到第H个要素成本份额方程。

证毕。

3 结束语

本文关于超越对数成本方程和要素成本份额方程组成系统结构模型的特征分析，不仅给出了构建该模型的严格证明，而且对于进一步拓展该类模型具有重要启示。比如，在式（1）中可根据需要进一步分析方程三次以上的项，以考察更多关于食品安全生产的经济现象。并且，不可观测的变量食品安全S均放入α，这正是面板方程的标志性特征，可将超越对数成本方程拓展为面板形式。至于α与其他解释变量是否相关，需采用相关的样本数据进行检验，决定式（1）的模型形式选择问题，即为混合效应、固定效应还是随机效应。意味着，式（1）可通过α的变化可以设定为多种形式，从而能够有效地解释当前各种文献对超越对数成本方程不同的设定形式，今后将在随后完成这些拓展研究。