基于云模型和蒙特卡洛方法的医院运营评价

刘 洋，李志强，韩 勇

（1.武汉大学中南医院；2.武汉大学医院管理研究所，武汉 400071）

0 引言

随着城市公立医院改革的逐步深入和医疗服务市场的不断发展，三级甲等医院作为我国医疗卫生服务的主体，其运营管理一直是卫生系统发展和改革的核心，也受到管理者和政策制定者的关注。根据我国《“十三五”深化医药卫生体制改革规划》要求，需要建立科学有效的现代医院管理制度，而运营管理作为医院管理的重要组成部分，其水平的提升直接关系到医院的健康可持续发展。这不仅是主管部门对医院进行客观考评的需要，更重要的是，通过对医院运营的全面分析，找出薄弱环节，清晰地把握医院的发展脉络，从而为医院发展战略目标的制定与及时调整提供重要依据。因此，如何有效分析医院的医疗服务质量和运营效率，对其运营状况进行全面评价，保证医院运营的良性循环成为一个重要的研究课题，对医院管理具有重要的现实意义。

学者们[1-4]以不同的方法对医院运营效率进行了分析与评价，从不同的角度总结归纳了医院运营中存在的主要问题，为医院运营效率评价做出了有益尝试。但医院运营管理评价是一个复杂、系统的问题，影响因素众多，既独立作用，又互相约束，仅采用简单方法或定性评价难以全面反映该复杂且不确定的过程。云模型作为一种定性和定量互换的模型，能处理不确定的数据，同时兼顾评价过程中的随机性和事物自身存在的模糊性；蒙特卡洛（Monte Carlo Method）则是借助随机抽样和统计实验对系统属性进行模拟，当前，已被广泛应用于数学、金融、工程等领域。本文提出一种云模型和蒙特卡洛相结合的医院运营综合评价方法，在指标体系构建和等级划分基础上，求得各医院所属运营评价等级，最后对评价指标进行敏感性分析，对敏感因素采取有效措施，进行重点控制管理，提升医院运营管理效率。

1 研究方法

（1）云模型

云模型所体现概念的整体特征用云的数学特征来反映。期望值Ex（expected value）指云滴的分布期望，代表定性概念的点；熵En（entropy）是定性概念的随机性度量，反映云滴的离散度；超熵He（hyper entropy）是对熵En的不确定性度量，由其模糊性和随机性决定，以上三个数学值Ex、En、He用来表达定性概念C的整体特征[5]。

（2）蒙特卡洛模拟

蒙特卡洛方法（MCM）与传统的确定性数值方法不同，它用随机抽样或统计模拟解决非确定性问题[6]，原理是构建一种服从指定函数分布的随机模拟模型，将模型的系统属性转化为数学期望[7]：

其关键是对目标分布f（x）进行重复性抽样实验，从而近似确定该x，通过抽样、试验计算该函数分布的统计特征值。通过大量次数的模拟，依照概率论的大数定理和中心极限定理，从而求出有价值的统计结果。

2 研究设计

2.1 运营评价体系构建

医院的运营建立在为患者提供优质的医疗服务之上，在追求经济效益的同时要注重成本控制，在公立医院综合改革的形势下，建立科学、全面的运营评价体系具有重要的意义。本文在查阅文献[8,9]的基础上，通过征求多家三甲医院管理专家的意见，结合医院评价标准和管理目标，构建了医院工作效率、医疗质量和经营成果3个方面的12个指标运营管理评价体系，如图1所示。

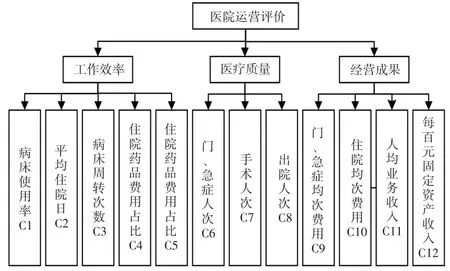
图1医院运营评价指标体系

2.2 评价指标权重确定

作为运营管理评价的关键内容，其指标的权重分配是否合理将直接影响到运营管理评价结果的准确性和科学性。本文采用客观赋权法，即通过提炼与分析各评价指标因素的数据集本身所涵盖的客观信息，从中寻找规律，以确定指标的权重。客观赋权法主要有三类：熵权法、标准离差法以及CRITIC法，本文采用熵权法计算指标因素的权重[10]。熵能够非常好地测量“不确定性”的问题，该方法的本质是充分利用指标因素的信息效用值，效用值越高，说明对评价的重要性也越大，能避免权重赋予的时候的主观性。首先确定已有的指标决策矩阵A=（dkj）m*n，参照给定的权重计算公式（1），可以用公式（2）来计算得出确定pkj，根据信息论使用公式（3）可以得到指标Bj的信息熵为Hj，当pkj=0时，规定pkjlnpkj=0。用公式（4）求出指标Bj的权重wj：

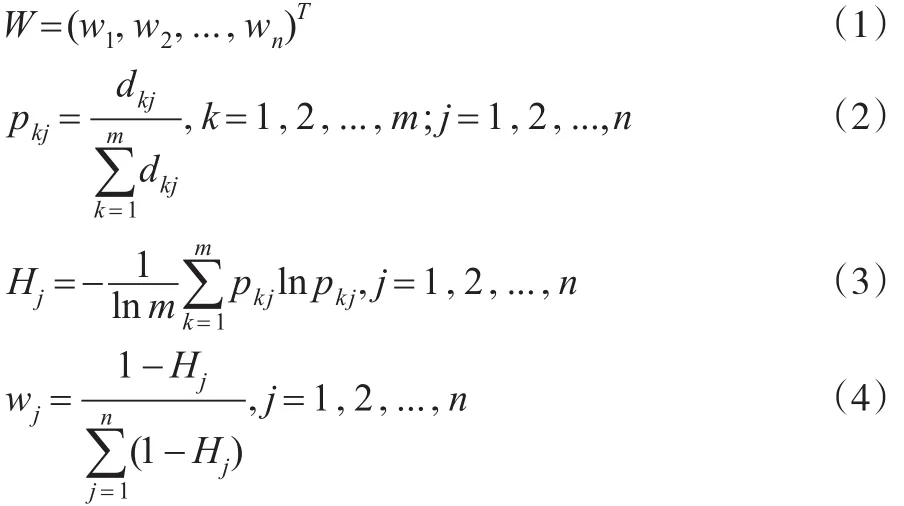
然后，通过熵权法求得运营管理评价体系中，各二级、三级指标的权重（见表1）。

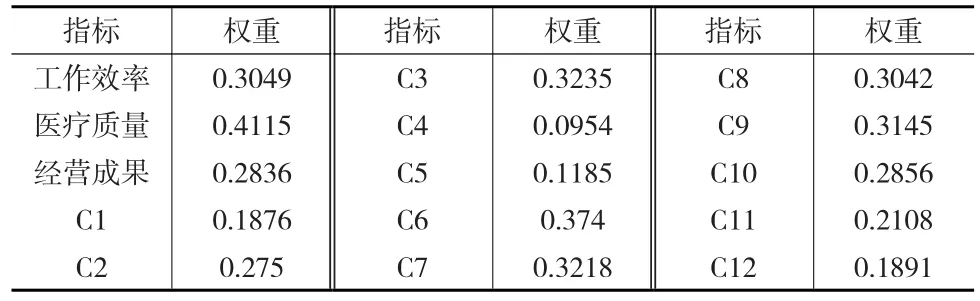
表1 各级评价指标权重

2.3 评价等级和范围

为全面分析运营的现状及发展趋势，便于采取对应的决策措施，本文结合国家卫计委公立医院改革文件以及相关文献，将医院运营的发展状态划分为A、B、C、D四个等级，并经过多次计算分析，将定性维度转化为定量维度对应为“0～1”“1～2”“2～3”“3以上”。具体等级如表2所示。

表2 运营评价等级划分

根据国家医院管理标准和政策，并结合湖北省多家三级甲等医院的年实际经营状况和以往的数据统计，同样将运营管理评价的指标从优秀到恶劣依次划分为四个等级：A级（优秀状态）、B级（良好状态）、C级（一般状态）、D级（较差状态）。确定各运营管理评价指标等级及区间划分：[Cmin,Cmax]，C1-C12为三级指标，如下页表3所示。

2.4 云模型特征值确定

步骤1：构建云模型[11]。

根据公式（5），为各指标所对应的每一等级构建模型，即确定各模型的特征值（Ex、En、He），其中s为常数。

步骤2：指标等级确定。

计算每个指标特征值对每一等级云模型的隶属度，第i特征值隶属于第j安全等级的隶属度μij。

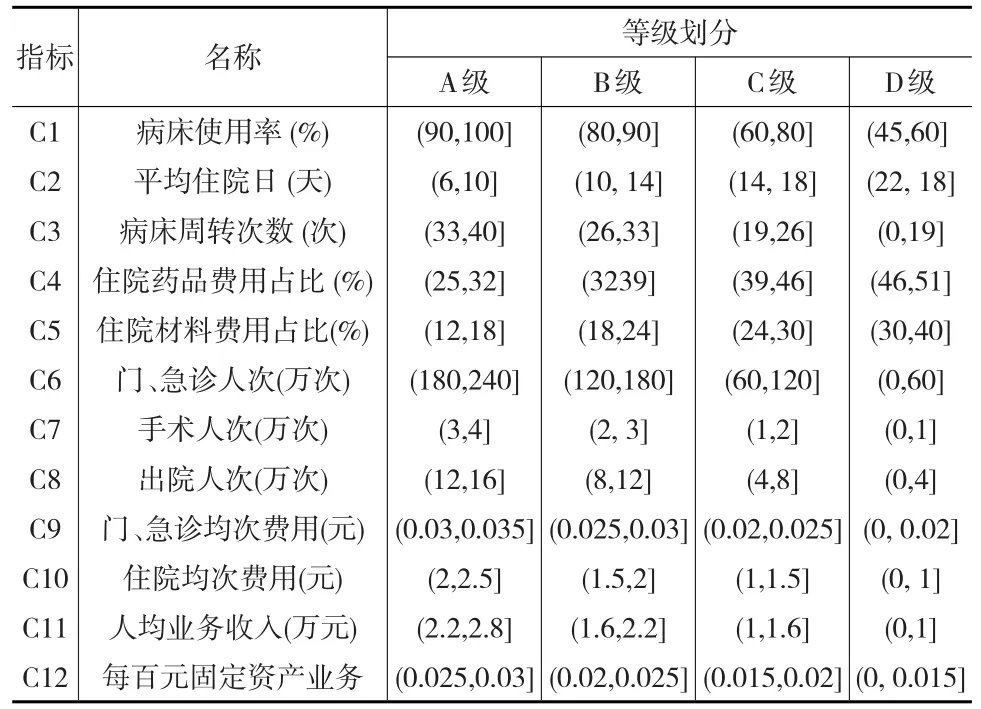
表3 运营评价指标及分级

其中，x为指标的监测值，Ex、En、s分别为对应等级云模型的三个参数。

步骤3：医院运营评价等级确定。

按照公式（8）用指标权重乘以隶属度μij[12]，例如前五个乘以权重得到“工作效率”的等级，后三个乘以各自权重得到“医疗质量”的等级，最后四个乘以各自权重得到“经营成果”的等级。

2.5 蒙特卡洛敏感性分析

利用Crystal Ball进行敏感性分析步骤如下[13]：根据医院运营评价指标模型，选择指标服从的分布方式，并在水晶球中输入；定义指标的假设单元和平均值的预测单元，预测单元即最终实际取值；确定模拟次数，至少应为1000次；运行蒙特卡洛模拟并获取结果。

3 实证检验

根据表4给出的武汉市四家床位规模2000以上的三级甲等综合性医院2016年运营数据，应用提出方法对四家医院的运营效益进行评价以验证方法的可行性和有效性，具体见表4。

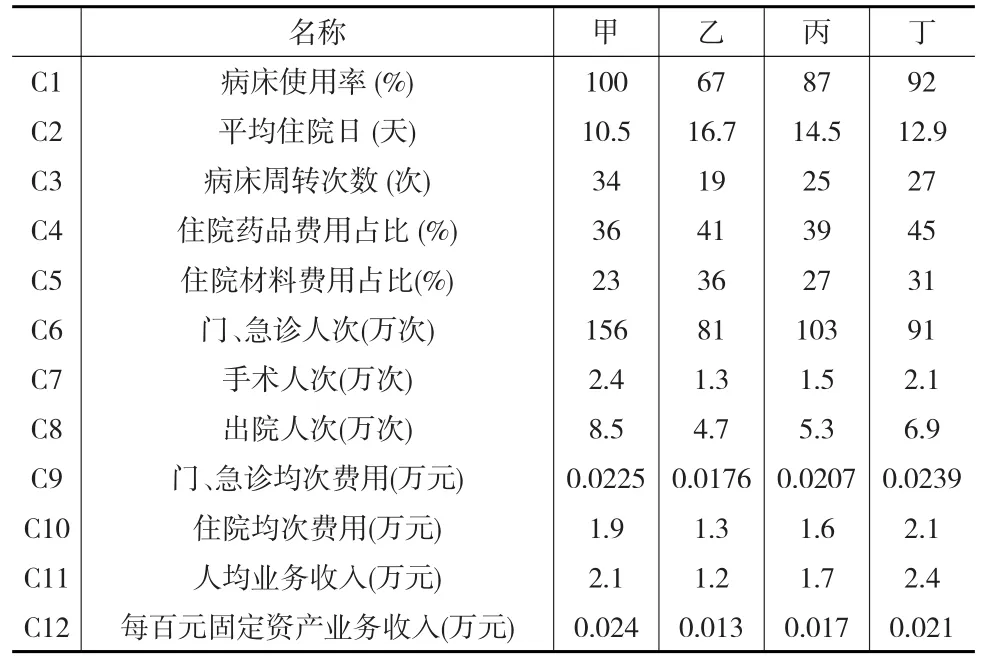
表4 四家三甲医院2016年运营数据

3.1 云模型分析

根据4个运营等级和范围，通过公式（5）求得12个指标的特征值，并建立评价区间对应的云模型（共48个），s取0.05，各指标的Ex、En、s见表5。

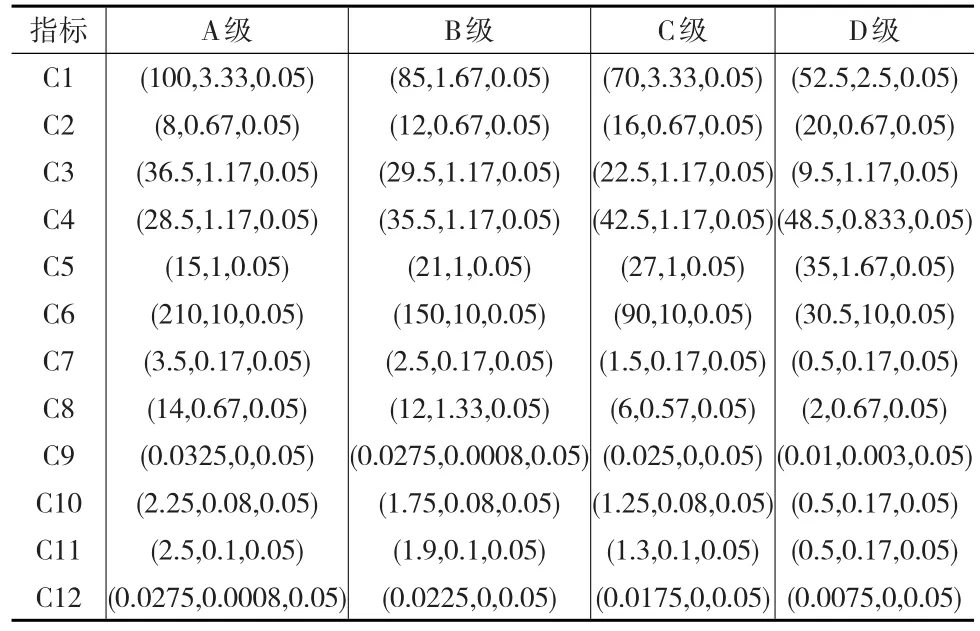
表5 运营因素指标对应等级云模型

本文采用Matlab法，根据每个指标云模型的（Ex、En、He）确定指标的运营评价等级，利用Matlab绘出4个运营状态正态云模型分布图，判断隶属区间及发展趋势。因篇幅有限，仅针对二级指标：医院工作效率，以甲医院C3病床周转次数为例，用Matlab绘图如图2所示。图中已标注较差、一般、良好和优秀四个运营等级区间，其中，甲医院2016年的病床周转次数的实际值模型，处于良好状态，未来有发展成为优秀状态的趋势。图3为乙医院2016年的病床使用率，四个运营等级区间也在云图中标注，其中，乙医院2016年的病床使用率的实际值模型，处于一般状态，未来有可能发展成为较差状态。

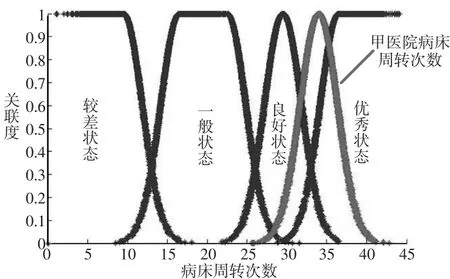
图2甲医院2016年病床周转次数正态云模型

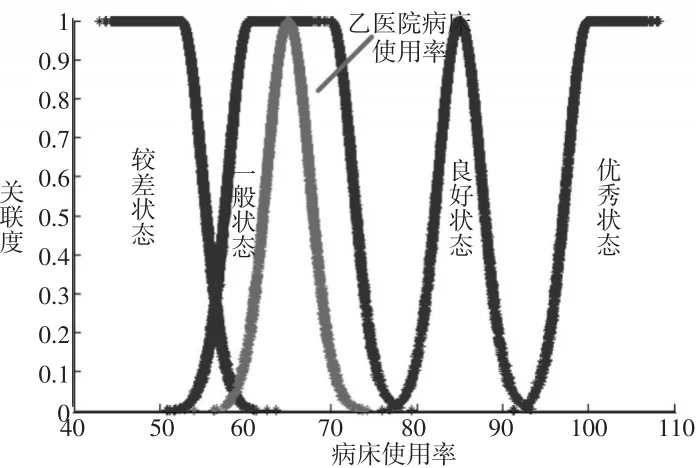
图3乙医院2016年病床使用率正态云模型

3.2 运营评价等级确定

根据公式（6）和公式（7）计算各指标等级的云模型对应每个运营状态的隶属度，再通过公式（8）求得甲、乙、丙、丁四家三甲医院的运营状况，如下页表6所示。

3.3 评价指标敏感性分析

为深入挖掘和分析影响医院运营状况的敏感性因素，实现运营控制管理的针对性和有效性，本文采用蒙特卡洛模拟对四家三甲医院进行敏感性分析。定义C1—C12为假设单元，预测单元为各医院运营状况的评分值，采用三角式定义指标的区间分布，最小值和最大值分别为最可能值的85%与115%，最可能取值附近的小区间为实际取值的分布，且距离最可能取值越近，则概率越大，模拟1000次。四家医院运营评价指标的敏感性贡献度见图4。

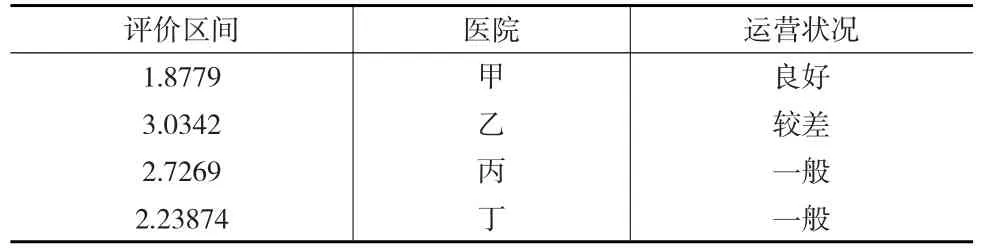
表6 2016年四家三甲医院运营状况

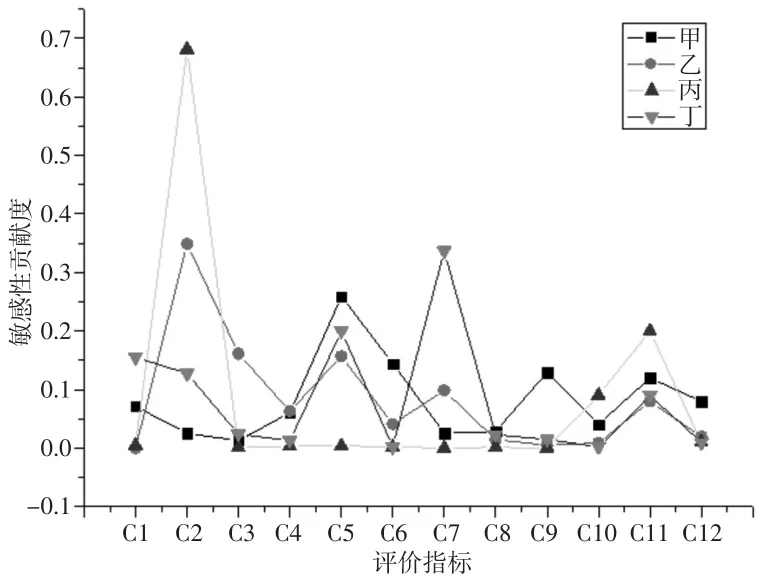
图4评价指标敏感性贡献度分布

从图4可以看到，甲、乙和丁医院均对住院药品费用占比（C5）的变动很敏感，对人均业务收入（C11）变动的敏感性次之；乙和丙均对平均住院日（C2）的变动最敏感；丁对手术次数（C7）最敏感。

4 结束语

本文将云模型理论初次引入到医院运营评价中，建立一套三级12个指标的医院运营综合评价体系，克服了指标选取的主观性和片面性，将运营状况划分成等级差异的四种状态，同时运用云模型方法分析各指标的发展趋势。最后通过武汉市4甲医院2016年的运营实例，求得各医院的运营状况，与实际情况基本一致，然后运用蒙特卡洛敏感性分析，找出影响其运营效率的主要因素，从而有针对性地加强监督考核与精细化管理，为医院的经营提供科学的依据。最终合理、高效地利用现有的各项医疗卫生资源，提高核心竞争力，改善医疗服务绩效，实现社会效益和经济效益最大化。