科技评价中因子分析信息损失的改进

俞立平，郭强华，张再杰

（1.浙江工商大学 统计与数学学院，杭州310018；2.云南大学 经济学院，昆明 650504；3.贵州财经大学 中国西部绿色发展战略研究院，贵阳 550025）

0 引言

因子分析是Spearman（1904）[1]提出的一种重要的客观评价方法，具有能够处理大量多指标数据、便于提取少数公共因子等优点，因此在科技评价中的应用越来越广泛。在中国知网中，查篇名“因子分析”的论文高达9000篇，而主题包括“因子分析”+“科技”的论文有1200多篇，包含“因子分析”+“期刊”的论文有200多篇。其他还有许多涉及采用因子分析的大学评价、学科评价、机构评价的论文。

因子分析评价也存在一些不足。在因子分析评价中，一般采用SPSS软件进行，通过降维将众多指标精简为少数关键因子，然后对这些因子按照方差贡献率大小进行赋权，最后进行加权汇总即得到评价总分，通常情况下需要累计方差贡献率大于85%，不过在实际应用中可以接受的方差贡献率在80%左右即可。因子分析方法评价有三个问题：第一，在科技评价中，往往采用2～4个关键因子进行评价，目前的实证论文中，累计方差贡献率很少超过90%，那么剩下的其他因子就被省略掉了，存在着较大的信息损失，这是不合理的。第二，在评价对象众多的情况下，区分度会很低，评价时是否舍弃其他公共因子对评价结果影响较大，对于增加其他公共因子能够得到排名改善的评价对象而言，会认为评价不够公平。第三，在计算机技术日益发达的今天，如果说降维作用不可忽视外，那么省略其他因子精简计算根本就没有必要。以上三个问题的根源主要还是因子分析评价对原始数据信息的遗弃。对因子分析评价存在的问题进行深入分析，不仅可以优化因子分析方法，深化对其应用的理解，丰富因子分析理论，而且在实际应用中也便于对因子分析方法的选择，提高评价的科学性、适用性和公众接受程度。

在科技评价中，因子分析涉及范围非常广泛，绝大多数领域均有采用因子分析的研究文献。李子伦（2014）[2]从产业体系的科技创新能力、人力资本积累水平与资源利用效率水平三个方面建立指标体系，采用因子分析对金砖国家产业结构升级水平进行评价。顾雪松等（2010）[3]从科技投入、科技产出、科技对经济与社会的影响三个方面选取科学技术评价指标，利用R聚类与因子分析相结合的方法定量筛选指标，构建了科学技术综合评价指标体系。董晔璐（2015）[4]运用因子分析法对我国31个省份的高校科技创新能力进行分析与评价。黄斌等（2013）[5]运用因子分析模型对江苏省13个地级市的科技服务业竞争力进行评价。夏文莉（2013）[6]通过因子分析法分析了科研学术不端行为的有关要素，认为科研诚信和科技评价紧密相关。

学术期刊评价中因子分析也得到了广泛的应用。吴涛等（2015）[7]采用6个文献计量指标，通过对WoS数据库和Scopus数据库共有的1881种医学进行评价，寻找公共因子。郑丽霞（2014）[8]选取2014年汤森路透社JCR中SCI收录的20种期刊数据为样本，采用因子分析法对其8个评价指标进行综合评价。贺颖（2007）[9]采用因予分析的方法，寻求管理类学术期刊引文的基本特点和一般规律，同时透视管理类期刊的学术水平和期刊质量及其学术影响力。柴玉婷和温学兵（2016）[10]以2015版中国科技期刊引证报告（扩刊版）中的14个量化评价指标为依托，利用因子分析法对42所师范大学理科学报的学术影响力进行分析排名。刘岩（2016）[11]利用多维面板数据，采用因子分析法对中国图书情报学19种核心期刊的发展态势进行了研究。何莉等（2014）[12]采用11个文献计量指标，运用因子分析法，对安徽省高校自然科学学报的学术影响力水平进行综合评价。

关于因子分析方法应用的注意事项与存在的问题，MacCallum等（1999）[13]探讨了不同样本大小及不同变量公共方差情况下，所得的因子负载的精确程度，认为因子分析在大样本下应用更好。Fabrigar等（1999）[14]认为因子分析中每个因子至少应包含4个或是更多的变量才能确保因子被有效识别，指标数量不能太少。Edward（1992）[15]认为因子分析与主成分分析的前提条件是数据必须服从正态分布，而实践中这种条件很难具备。林海明（2006）[16]从找因子分析精确解的角度，以主成分分析理论为基础，应用矩阵运算方法，建立了新的因子分析模型，消除了理论假设的误差，给出了因子分析模型的精确解，找到了因子分析与主成份分析的关系式。熊国经等（2016）[17]认为采用多属性评价方法评价学术期刊会遇到指标间多重共线性以及指标权重不确定的影响，采用因子分析确定关键因子，采用熵权法确定权重，最后用加权TOPSIS进行评价。俞立平和刘爱军（2014）[18]根据因子分析隐含的假设是评价指标必须服从正态分布的原理，认为在期刊评价指标普遍呈幂律分布的情况下，最好将评价指标取对数后再进行评价，否则会扩大系统误差。靖飞和俞立平（2012）[19]针对因子分析和主成分分析在期刊评价中存在的问题，提出了一种新的学术期刊评价方法——因子理想解法，首先采用因子分析筛选出关键因子，然后确定各关键因子的权重，在此基础上将关键因子标准化后采用加权TOPSIS进行评价。

从现有的研究看，因子分析在科研机构评价、大学评价、学术期刊评价、科研人员评价等科技评价中得到了广泛应用，是迄今为止应用较多、影响较广的客观评价方法之一。关于因子分析评价的适用条件、评价方法可能存在的问题，现有的研究总体不多，有待进行深入。本文在对因子分析存在问题分析的基础上，提出了一种新的评价方法——完全信息因子分析法，并以JCR经济学期刊为例，比较采用传统因子分析评价与完全信息因子分析评价结果的区别。

1 因子分析评价存在的问题及改进

1.1 因子分析方法评价存在的问题

1.1.1 科技评价方法的分类

在科技评价中，根据评价数据的确定性情况，宏观上有两大类评价方法（见图1）。第一大类是确定性评价方法，从信息完全度角度，又包括两类，一类是完全信息评价方法，大多数评价方法均是如此，比如层次分析法（AHP）、理想解法（TOPSIS）、熵权法、灰色关联法等，其特点是尽管评价方法不同，但是评价结果严格反映评价指标数据的信息。另一类是不完全信息评价方法，如因子分析、主成分分析、粗糙集等，其特点是评价结果只反映了评价指标的大部分信息，主成分分析和因子分析均采用特征根大于1的主成分或主因子来进行评价，粗糙集则干脆通过约简进行了指标精简，删除了一些指标。第二大类评价方法称为模糊性评价方法，又包括指标数据模糊或权重数据模糊两类。当然这并不是本文重点关注的范畴，因为在科技评价中，绝大多数评价是确定性评价方法，本文重点分析确定性评价中因子分析方法存在的问题。

图1评价方法分类

1.1.2 因子分析方法评价的优点

在科技评价中，从因子分析方法的优点分析入手，可以分析不完全信息的原因，在此基础上进行改进。

第一，因子分析方法是一种客观评价方法。在科技评价中，如果采用主观方法确定权重，则重复性往往较差，换一批专家权重设定肯定不一致，当然评价结果也不一致，这导致许多诟病，认为主观评价方法不公平，而客观评价方法不需要设定指标权重，完全根据客观数据来评价，如果数据确定，结果就确定，减少了人为因素干扰评价结果的可能，因此有一定的价值。

第二，因子分析方法能够降维。因子分析通过数十甚至上百个评价指标的处理，能将其降维为少数公共因子，这少数公共因子中包括了原始数据的大量信息，而且可以在现实世界中对其命名，化繁为简，便于总结提炼。在指标众多的情况下，单靠人的大脑对指标分类是非常困难的，何况有些评价指标具有多重含义，比如即年指标，既可以用来表示期刊影响力，也可以用来表示期刊的时效性，究竟将其归为哪一类？

第三，因子分析提取的公共因子不相关。这一点是因子分析的又一个重要优点，在技术经济分析中，变量之间的相关容易造成多重共线性，因子分析彻底解决了这一问题，而且每个因子均具有经济含义，这是非常了不起的算法。

第四，因子分析方便计算，运用SPSS软件，将处理好的数据导入，短短数分钟可以得到评价结果，这是许多其他评价方法难以做到的。

1.1.3 因子分析方法评价存在的问题

以上四个优点是因子分析法得到广泛运用的原因，但是因子分析方法也带来了新的问题：

第一，客观评价一定就没有问题吗？虽然客观评价方法优点众多，但是如果评价不能体现出管理者的意志，评价不能为管理服务，那么这种评价又有什么意义？比如科技创新评价中，研发投入是最重要的指标，但哪种客观评价方法怎么能保证该指标最重要？虽然因子分析方法中回避了直接权重的概念，但采用俞立平等（2010）[20]提出的模拟权重计算方法，将因子分析评价结果与评价指标进行回归，对回归系数进行标准化就可以得到各评价指标的模拟权重。这样因子分析作为客观评价方法不需要人工赋权的优点就要打折扣，因为它不能保证评价为管理服务，不能保重关键指标的重要性。

第二，因子分析方法丢失了原始数据的大量信息。由于因子分析方法评价时只采用少数公共因子进行评价，这样其他因子中的大量信息就会舍弃。这种处理方法是值得商榷的，从信息量看，少数公共因子基本能够解释所有数据信息量的80%以上，总体上似乎没有问题，但对评价个体就不同了，在评价对象众多、区分度较低的情况下，是否舍弃其他不重要的公共因子对评价结果就会产生较大的影响。比如在大学评价中，采用因子分析对全世界大学进行排名，采用少数公共因子和采用全部公共因子评价大学排名肯定会有较大不同。

降维是因子分析的最大优点，但是降维的目的是为了便于分析，不一定是为了评价，或者说，为了对数据进行更为精准的分析，可以采用因子分析方法进行降维，但不一定要采用因子分析进行评价。根据以上分析，因子分析适合降维这是无可争议的，但是因子分析未必就适合评价。

第三，精简计算在现代是没有意义的。降维可以精简计算这是肯定的，尽管提取公共因子的过程略显繁琐，但通过SPSS软件非常方便。采用少数公共因子评价与采用全部公共因子评价增加的计算量可以忽略不计。在科技评价中，随着计算机技术、软件技术日趋成熟，加上大数据、云计算等新一代信息技术的普及，已经没有必要考虑科技评价的算法了，最重要的是评价方法是否科学、合理、合适、公平。

第四，因子分析并没有降低评价成本。有些不完全信息评价方法是有其存在意义的，比如说粗糙集，评价指标个数众多必然意味着评价成本增加，在这种情况下，通过指标约简虽然牺牲了部分信息，但是大大降低了评价指标数量，节约了评价成本。但是因子分析方法通过降维并没有减少评价指标，当然也没有降低评价成本，因此不能从节省成本的角度肯定因子分析方法。

1.2 完全信息因子分析法

所谓完全信息因子分析（All Information Factor Analysis，AIFA），就是在因子分析评价中，采用全部公共因子进行评价，而不是少数几个公共因子。这样做法的最大好处是：

第一，一点也不牺牲原始数据信息，做到了评价方法的公平公正，容易被公众所接受。

第二，计算简单，可以继续基于SPSS软件进行，不同的是在提取公共因子时采用全部可能的公共因子，也就是说公共因子的数量与评价指标的数量是一样的。

第三，并不影响因子分析的其他优点。比如降维，在评价过程中，同样可以通过降维找到少数几个公共因子，计算方差贡献率，分析哪些指标对评价影响较大等等，只不过不采用少数几个公共因子评价而已。

1.3 最大信息因子分析法

在因子分析中，根据方差贡献率设定权重不一定是可取的，虽然这种权重确定方法本质上是一种客观赋权法，完全根据数据说话，但不一定就是最有效的赋权方法。因子分析中因子的权重取决于相关指标的数量，比如期刊评价，如果影响力指标较多，时效性指标较少，那么第一因子肯定是影响力，权重最高，第二因子就是时效性，权重要低一些。假设我们现在评价的目的主要是评价期刊的学术活力，那么影响力指标的权重必须低于时效性指标，所以客观赋权就不一定合理了。

采用因子分析提取公共因子个数的上限是由评价指标的数量决定的，但是如果从对公共因子命名、具有经济含义的角度，公共因子的数量又是有限的。究竟如何选取，可以设置最大公共因子后根据旋转矩阵来进行判定，此时得到的可以解释的公共因子数量往往比传统因子分析评价多，但肯定少于所有公共因子数量，可以将这种采用可解释公共因子进行评价的方法称为最大信息因子分析法（Maximum Information Factor Analysis，MIFA）。权重设定不必采用方差贡献率，可以通过专家会议法等主观评价方法确定。

根据最大信息因子分析法获得所有的可解释和命名的公共因子后，由于这些公共因子互不相关，因此便于专家进行赋权，然后进行加权汇总，这样不仅最大限度地保留了原始数据的信息，而且体现了评价的管理目的，具有较强的实践意义。

2 评价实证

2.1 数据来源与评价指标设计

为了比较因子分析评价、完全信息因子分析评价、最大信息因子分析评价的区别，本文以JCR 2015经济学期刊评价为例进行分析。2015年JCR经济学期刊共有333种，数据量较大，便于因子分析。JCR评价指标共有11个，分别是：总被引频次（Z1）、影响因子（Z2）、他引影响因子（Z3）、5年影响因子（Z4）、即年指标（Z5）、特征因子分值（Z6）、论文影响分值（Z7）、标准化特征因子（Z8）、被引半衰期（Z9）、引用半衰期（Z10）、影响因子百分位（Z11）。

由于部分期刊评价指标数据缺失，原因包括期刊办刊年度较短、0引用等，需要进行数据清洗，经处理后还有278种期刊，指标数据描述统计如表1所示。

表1 指标描述统计

2.2 实证结果

2.2.1 因子分析法评价的旋转矩阵与载荷分析

首先采用因子分析法进行评价，KMO检验值为0.839，bartlett检验值为7933.350，相伴概率为0.000，说明适合采用因子分析方法进行评价。旋转矩阵如表2所示，特征根大于1的共有两个公共因子，第一公共因子的方差贡献率为56.95%，第二公共因子的方差贡献率为17.37%，合计74.32%。除了即年指标Z5、被引半衰期Z9、引用半衰期Z10属于第二公共因子外，其他指标均属于第一公共因子，所以第一公共因子可以命名为期刊影响力因子，第二公共因子可以命名为期刊时效因子。

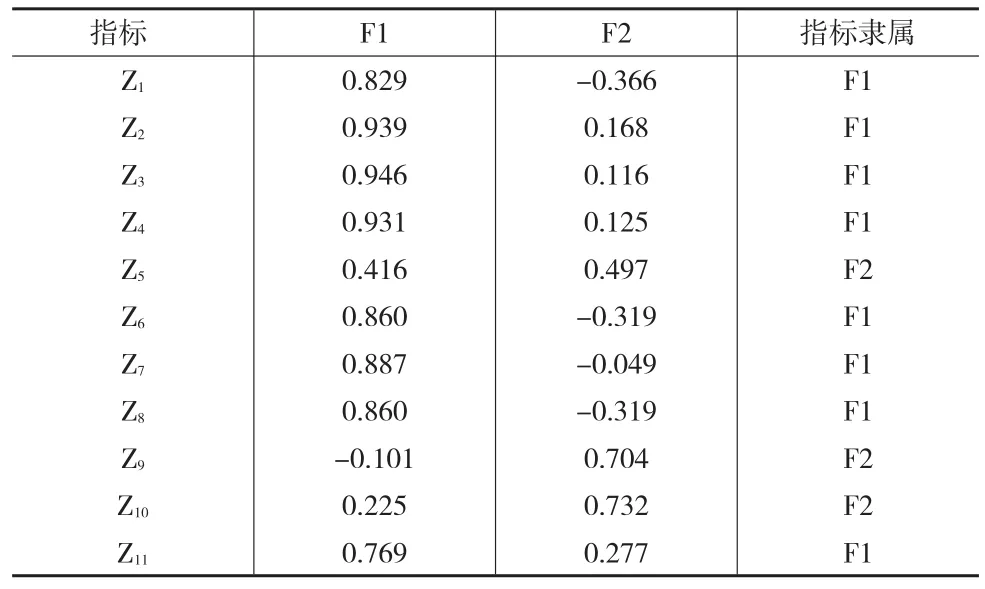
表2 因子分析旋转矩阵

2.2.2 完全信息因子分析法评价的旋转矩阵与载荷分析

下面采用完全信息因子分析法进行评价。由于采用完全信息，所以在提取公共因子时，采取可能极大值原则，11个评价指标选取11个公共因子，旋转矩阵如表3所示。虽然提取了11个公共因子，但是所有指标只能归到5个公共因子中，第一公共因子包括影响因子Z2、他引影响因子Z3、5年影响因子Z4、论文影响分值Z7、影响因子百分位Z11，可以将其命名为影响因子类指标；第二公共因子包括总被引频次Z1、特征因子Z6、标准特征因子Z8三个指标，可以将其命名为期刊总体影响力指标；第三公共因子是即年指标Z5，为当年时效性指标；第四公共因子是引用半衰期Z10；第五公共因子是被引半衰期Z9。

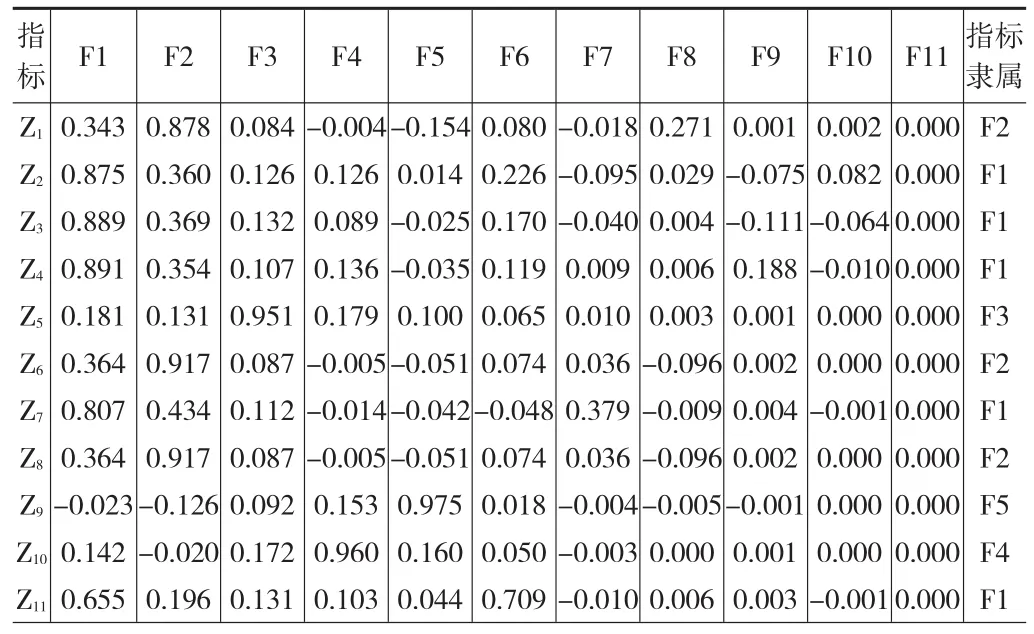
表3 完全信息因子分析旋转矩阵

从平方载荷旋转旋转和看（表4），前5个因子的累计方差贡献率为91.47%。后几个因子的方差贡献率很小，F11几乎为0，F10仅为0.098%，F9仅为0.487%，F8仅为0.848%，均不到1%。当然在具体评价时，为了保持原始数据信息的完整性，全部纳入进行评价。

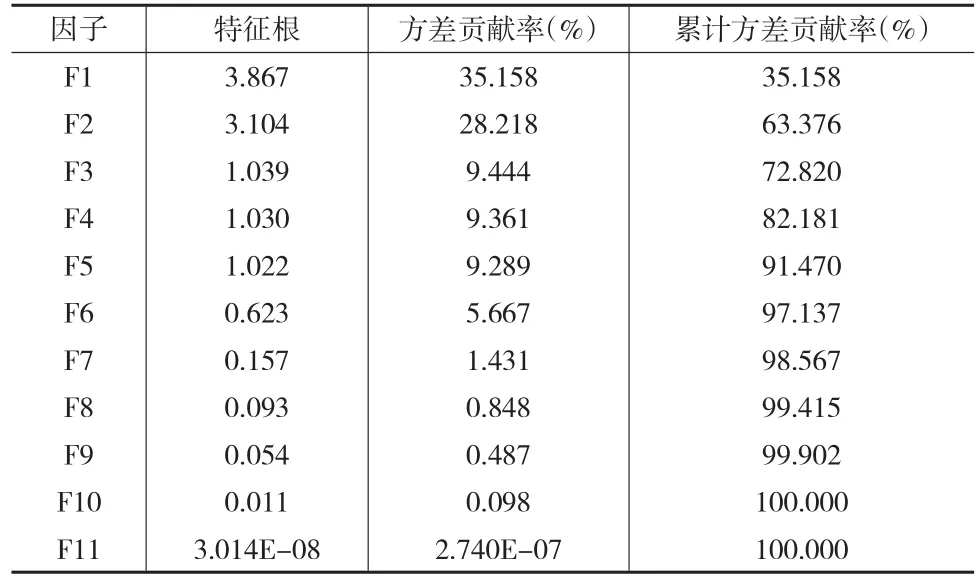
表4 平方载荷旋转和

2.2.3 两种方法评价结果比较

因子分析与完全信息因子分析的评价结果如表5所示，由于期刊较多，仅列出了因子分析排名前30的期刊。两种评价方法的评价结果相差较大，排名前30的期刊区分度本来就大，正常情况下应该具有一定的评价鲁棒性，即评价方法的差异不会带来评价结果排序的较大变化，但在实际情况下并非如此。

表5 评价结果比较

因子分析评价与完全信息因子分析评价的散点图如下页图2所示，很明显可以看出两者正相关，通过相关系数分析发现，两者的相关系数为0.866，并且通过了统计检验，具有较高的相关度。但是相关度较高是从总体分析的，对于个体而言，两种评价方法评价结果还是相差较大的。

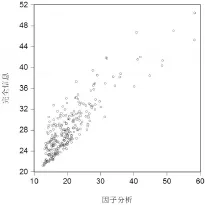
图2完全信息因子分析与因子分析评价结果对比

2.2.4 最大信息因子分析法评价

从完全信息因子分析的旋转矩阵看，11个评价指标中共提取了5个公共因子，本文以这5个公共因子为基础采用最大信息因子分析法进行评价，为了和完全信息因子分析评价结果进行比较，这里继续采用方差贡献率赋权，评价结果如表6所示。同样给出前30种期刊，可以很明显看出，尽管评价结果排序有所区别，但是评价结果排序的一致性较高。

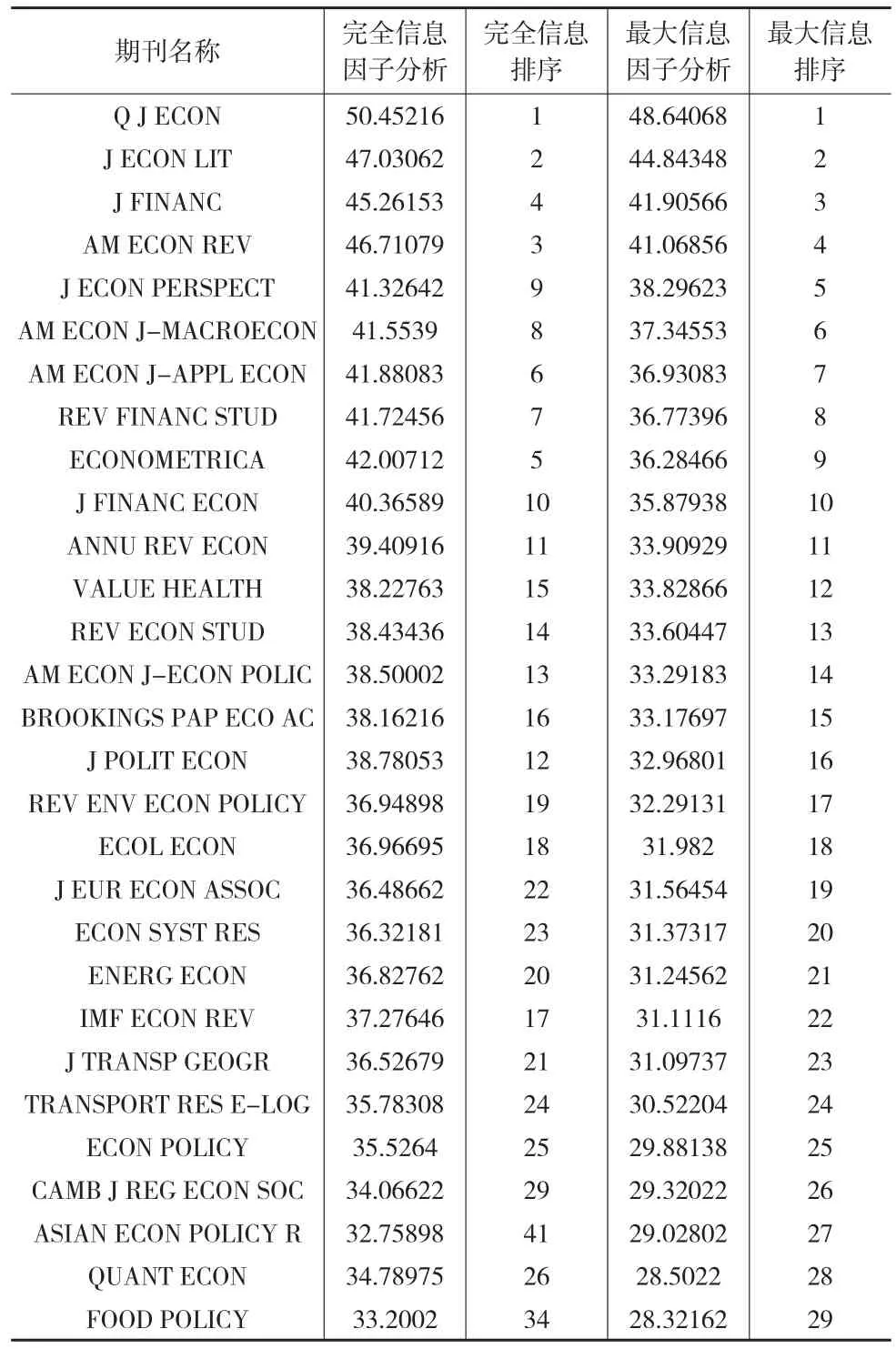
表6 完全信息因子分析与最大信息因子分析结果比较

同样汇出完全信息因子分析评价结果与最大信息因子分析评价结果的散点图（见图3），两者不仅相关度高，而且几乎呈现一条直线，两者的相关系数高达0.982，说明最大信息因子分析评价虽然也牺牲了原始数据的部分信息，但是与因子分析方法评价相比，已经得到很大提升，关键是通过其他方法赋予权重体现了评价为管理服务，具有较强的适用性。

图3完全信息因子分析与最大信息因子分析评价结果对比

3 结论与讨论

（1）因子分析法评价会损失原始数据的大量信息

因子分析法评价由于采用少数公共因子进行加权汇总评价，这样会丢失原始数据的大量信息，从而影响评价结果。本文分析发现，因子分析法通过降维增加了公共因子的解释能力，从而便于进行深入分析，但是降维本身并没有精简计算，也没有减少评价指标的数量从而降低评价成本，因此以牺牲原始数据信息为代价的因子分析评价并不具备太多的优势。

（2）完全信息因子分析评价弥补了因子分析评价的信息不足

完全信息因子分析评价克服了传统因子分析评价的弊端，完全不会牺牲原始数据信息，而且保留了因子分析方法的优点。本文研究发现，虽然传统的因子分析评价结果与完全信息因子分析评价结果高度相关，但是对于评价对象个体而言，两种评价方法结果排序相差较大，不利于科技评价的公平公正。

当然，完全信息因子分析完全采用方差贡献率大小进行赋权是值得商榷的，这是所有客观评价方法面临的问题。

（3）最大信息因子分析评价方便主观赋权

最大信息因子分析法在尽可能保持原始数据信息的情况下，比传统因子分析提取了更多的公共因子，而且这些公共因子互不相关，这样在此基础上，可以根据评价目的与管理要求采用其他方法确定权重进行评价，克服了完全信息因子分析完全进行客观赋权的不足。

但最大信息因子分析虽然也牺牲了部分原始数据的信息，但总体上这种影响较小，不像因子分析评价那样牺牲的信息量较大。

（4）对于传统因子分析应该重分析轻评价

因子分析方法的优点无可替代，比如降维技术、客观的洞察力、公共因子不相关等，因此因子分析更适合对数据进行分析，但是从评价的角度，这并不是因子分析的强项，但可以借用。本文在因子分析的基础上提出了完全信息因子分析与最大信息因子分析两种评价方法，前者不会牺牲原始数据的任何信息但不宜主观赋权，后者在尽可能少牺牲原始数据信息的情况下结合主观赋权进行评价，各有特点，可以根据需要灵活选用。