基于极端学习机的NOx预测模型样本特性研究

申志文, 李庆伟

(上海电力大学 能源与机械工程学院, 上海 200090)

燃煤发电在我国乃至世界范围内仍然是一种重要的发电形式,而煤炭燃烧是NOx的主要来源之一[1-2]。为实现火力发电厂的超低排放,我国环保部门制定了严格的NOx排放标准[3]。燃烧优化技术是一种简单、高效、廉价的燃煤电厂NOx减排技术,精准的NOx排放模型是燃烧优化技术的基础[4]。

锅炉燃烧系统具有非线性和强耦合的性质,难以用机理建模的方法建立准确的NOx排放预测模型。随着人工智能的兴起,许多学者开始利用机器学习建立NOx排放预测模型,常用方法有人工神经网络[5-6]和支持向量机[7-8]。

HUANG G B等人[9]提出的极端学习机(Extreme Learning Machine,ELM)是一种重要的NOx排放预测建模方法。与传统神经网络相比,ELM具有泛化性能好、学习速度快、精度高等优点[10]。目前,针对输入权值和隐藏层阈值优化的研究较多,常用的优化方法有风驱动算法[11]、混沌分组教与学优化算法[12]、量子粒子群算法[13]。

朱志华等人[14]对非小细胞肺癌病人术后生存时间进行了预测分析,训练样本数目分别为110,130,150。范宇辰[15]针对一种Benchmark分类问题,利用仿真实验探讨了训练样本个数、隐藏层节点数、输入层权值以及隐藏层节点偏置量4个重要参数对ELM分类器性能的影响程度。为了解决分类学习缺乏足够的缺陷样本的问题,MA L Y等人[16]提出了高斯混合模型密度估计的ELM,以检测锂离子聚合物电池的电池片中的气泡缺陷,能够在不同的训练样本数量下保持优异的精度性能。

火电厂NOx排放预测建模属于多维、强耦合的复杂问题,目前尚未有ELM样本特性分析的相关工作。本文在总样本一定的前提下,研究了测试样本数对NOx预测性能的影响,并寻找最佳的测试样本数。

1 极端学习机

ELM通过随机产生的输入权值和隐藏层阈值,利用最小二乘法和M-P广义逆矩阵求解输出权值。其网络结构如图1所示。

图1 ELM网络结构示意

对ELM的描述如下。

k=1,2,3,…,N

(1)

b——隐藏层各节点的阈值矩阵,b=[b1,b2,…,bl]T。

式(1)可以简化为

Hβ=T

(2)

(3)

β=H+T

(4)

式中:H——隐藏层输出矩阵;

β——输出权值矩阵,β=[β1,β2,…,βl]T;

T——N×1维的目标输出据阵,T=[t1,t2,…,tN]T。

ELM的学习步骤可总结如下:首先,设置激活函数和隐藏层节点数;其次,随机生成输入权值和隐藏层阈值;再次,利用式(3)计算隐藏层输出矩阵H;最后,利用式(4)计算输出权值矩阵。

2 基于ELM的NOx预测样本特性研究

训练样本数过多会影响预测模型的训练速度,数量过少则会影响预测模型的性能。本文基于ELM建立预测模型,研究在总样本数目一定的条件下,测试样本数目对预测性能的影响。选择测试集均方根误差(Root Mean Squared Error,RMSE),即预测样本RMSE作为性能指标,公式为

(5)

预测样本的特性研究具体步骤如下:

(1) 设置隐藏层节点数和激活函数类型等神经网络参数;

(2) 根据不同测试样本数划分训练集和测试集;

(3) 利用训练集训练ELM模型;

(4) 利用训练好的ELM模型对训练集和测试集样本进行预测;

(5) 计算训练集和测试集样本的RMSE;

(6) 返回步骤3,直到实验次数达到31次;

(7) 计算当前测试集样本数下测试样本中位数RMSE;

(8) 返回步骤2,直到测试样本数达到最大值;

(9) 根据不同测试集样本数下测试样本中位数RMSE,选出最优测试样本数。

上述研究方法的流程如图2所示。

图2 基于ELM的预测样本特性研究流程

3 实验结果与分析

3.1 实验数据与参数设置

采用文献[17]中的数据,对330 MW电站锅炉进行实验。选取负荷、给煤机转速、一次风速、二次风速、排烟氧量、燃尽风挡板开度和煤质等26个参数进行变工况实验,工况1～工况3、工况4、工况5～工况6,工况7～工况14和工况15～工况20分别燃用不同的煤种。

ELM的隐藏层激活函数为sig函数,隐藏层节点的数量设置为30,分别选取不同数目的测试样本重复实验31次。

3.2 结果与分析

测试样本中位数RMSE随样本个数的变化趋势如图3所示。由图3可以看出,随着测试样本数的增加,测试样本中位数RMSE整体呈现增长的趋势,当测试样本数为2个时,测试样本中位数RMSE最小,此时,训练样本数为18个。

图3 测试样本中位数RMSE随样本数的变化趋势

为进一步研究样本数目对预测性能的影响,对31次预测样本RMSE进行观察。预测样本RMSE随测试样本数目变化趋势如图4所示。对于训练集,测试样本数目的影响较小,均能达到较好的预测效果;而对于测试集,随着测试样本数的增加,训练样本数减少,RMSE呈明显增大的趋势。当测试样本数为2个时,预测样本RMSE整体较小,且波动范围相对较小。

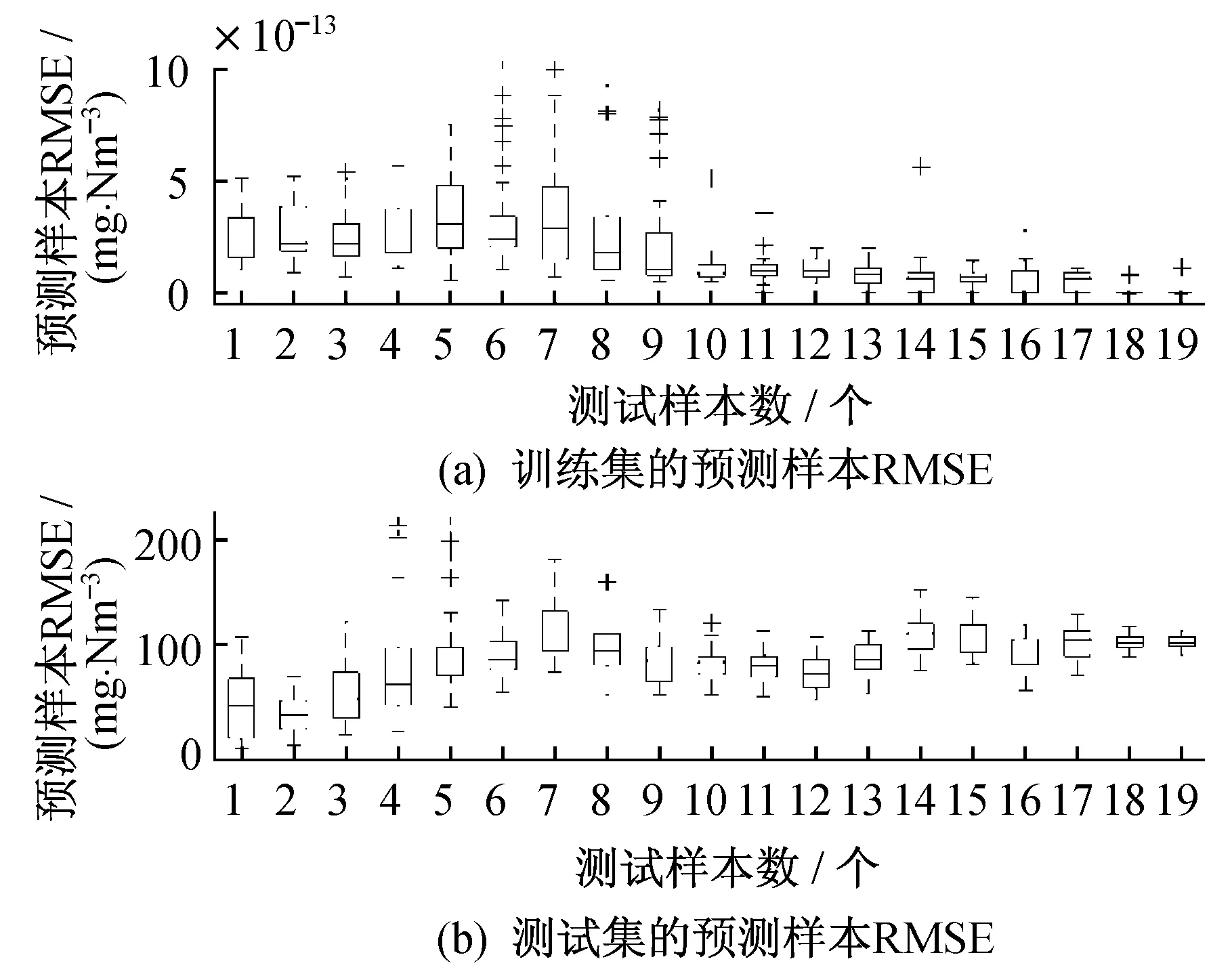
图4 31次实验预测样本RMSE随测试样本数的变化趋势

当测试样本数为2个时,对训练样本和测试样本进行预测,其预测绝对误差结果如图5所示。其中,样本编号1和2的样本为测试样本。由图5可以看出,模型在训练样本上的预测性能较好,在测试样本上的误差也较为理想,但泛化性能还存在进一步提升的空间。

图5 测试样本数为2个的31次实验预测绝对误差分布

4 结 语

电厂锅炉燃烧优化的关键是建立准确的预测模型。本文建立了基于ELM的NOx排放预测模型,并研究了不同测试样本数对该模型性能的影响。实验结果表明,随着测试样本数的增加,测试样本中位数RMSE整体呈现增长的趋势。当测试样本数为2个时,预测的测试样本中位数RMSE最佳,预测样本RMSE整体较小,且波动范围相对较小,但模型的泛化性能还存在进一步提升的空间。