一种基于深度学习的双JPEG图像压缩检测算法

楚雪玲, 魏为民, 华秀茹, 李思纤, 栗风永

(上海电力大学 计算机科学与技术学院, 上海 200090)

盲取证技术在不知道原始来源的情况下,利用统计和几何特征、插值效应或特征不一致可验证图像/视频的真实性。由于JPEG压缩可能会覆盖数字篡改的某些痕迹,因此许多盲取证技术仅对未压缩的图像有效。然而,大多数媒体捕获设备和后期处理软件(如PHOTOSHOP),以JPEG格式输出图像,而且互联网上的图像大多是JPEG格式的。因此,对JPEG压缩鲁棒性研究的盲取证技术至关重要。原始JPEG图像(质量因子为QF1)被篡改后通常需要重新压缩,即将经过数字篡改后的伪造图像以不同质量因子(QF2)的JPEG格式重新存储,可能会引入双重JPEG压缩的证据。近年来,许多成功的双JPEG图像压缩检测算法被提出。文献[1-2]分析了篡改前后的双量化(Double Quantilization,DQ)效应,发现经过两次量化的图像区域的离散余弦变换(Discrete Cosine Transfrom,DCT)系数直方图一般呈现周期性,不同于单量化区域的DCT系数直方图。文献[3]识别了DCT系数在时域与频域的周期性压缩伪迹,可以检测块对齐和非对齐的双JPEG压缩。文献[4-5]提出单压缩图像的DCT系数一般遵循Benford定律,而双压缩图像的DCT系数则违反了Benford定律。在文献[5]中,采用DCT首位统计特征和支持向量机(Support Vector Machine,SVM)分类器相结合来对双JPEG压缩检测。文献[6]将双JPEG压缩应用于隐写术,使用的特征是从低频DCT系数的统计中得到的,不仅对普通的伪造图像有效,而且对使用隐写算法处理的图像也有效。

然而,上面讨论的算法有一个共同点,它们只估计图像的压缩历史,而不能准确地指出操作了哪个区域。文献[7]提出的算法是第一个通过分析DCT系数直方图中隐藏的DQ效应来自动定位局部篡改区域的算法。该算法使用贝叶斯方法估计了单个8×8块被篡改的概率,得到的块后验概率图将显示篡改(单压缩)区域和未修改(双压缩)区域的视觉差异。为了更准确地定位篡改区域,文献[8]利用先验知识,即篡改区域应该是光滑的、聚类的,并使用图像分割算法最小化一个已定义的能量函数来定位篡改区域。文献[9]探索了一种新的基于特征的技术,使用残差的条件联合分布进行定位,不仅计算效率高,而且不受场景内容的影响。文献[10]基于文献[7]提出了更合理的概率模型,计算了每个8×8块被双重压缩的可能性,并结合一种估计初级量化质量因子的有效方法,比文献[7]具有更好的性能。基于改进的统计模型,文献[11]提出的方法既可以检测块对齐的压缩篡改区域,也可以检测块非对齐的压缩篡改区域。文献[12]基于DCT系数的第一个数字特征对图像拼接结果进行定位,并使用SVM进行分类。然而,当QF1>QF2时,这些方法的性能很差。

众所周知,深度学习方法可以自动学习特征并进行分类。利用卷积神经网络(Convolutional Neural Network,CNN)的深度学习在语音识别、图像分类或识别、文档分析、场景分类等领域取得了很大的成功。对于隐写分析,文献[13-14]利用CNN自动学习特征,捕捉对隐写分析有用的复杂依赖关系,结果令人大受鼓舞。事实上,使用CNN的分层特征学习可以学习特定的特征表示,具有深度模型的神经网络也可以有效地进行盲图像取证。

本文提出了一种利用CNN进行训练/测试的方法,来检测双JPEG压缩篡改的图像。为了增强CNN的效果,对DCT系数进行预处理。提取DCT系数的直方图作为输入,然后设计一维CNN从这些直方图中自动学习特征并进行概率结果分类,并与其他文献中的算法进行性能比较。

1 JPEG压缩背景介绍

利用图像软件篡改图像时,JPEG图像在篡改完成之后,可能会使用与原始图像质量因子QF1不同的质量因子QF2再一次压缩存储,即JPEG图像的双重压缩。应当注意,当QF1=QF2时,图像特性改变不明显。图像双压缩过程如图1所示。首先把原始JPEG图像解压缩,即先解码和反量化;再进行逆DCT变换;最后对解压缩的图像执行第二次压缩。

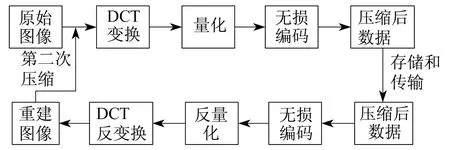
图1 双JPEG压缩过程

JPEG压缩是一种基于8×8块的方案,将DCT系数应用于输入图像的8×8块,然后量化DCT系数,并对其应用舍入函数。量化系数进一步通过熵编码进行编码,量化表对应每个特定的压缩质量因子QF,QF值为0～100的整数。QF值较低,表示丢失了更多的信息。DCT系数的量化是造成压缩图像信息丢失的主要原因。

2 算法模型设计

2.1 特征设计

对给定的JPEG图像进行预处理。首先,从JPEG头部提取其量化的DCT系数和最后一个质量因子,在实验中,只使用彩色图像的Y分量;然后,为每个DCT频率构造一个直方图。图像直流系数直方图的分布与交流系数的直方图不同,可能会给特征设计带来困难,因此本文算法只考虑交流系数。此外,如果将整个直方图直接输入到CNN分类器中,则训练操作会很复杂,原因如下:首先,CNN的输入特征维数必须一致,而直方图的大小总是变化的;其次,可能产生过高的培训计算成本。为了在不丢失重要信息的情况下降低特征向量的维数,选择每个直方图峰值附近的指定区间(可能包含大部分重要信息)表示整个直方图。使用以下方法提取低频下的特征集,具体如图2所示。首先,选取Zig-zag排列的第2～10个DCT系数构建特征集,仅取对应于{-5,-4,…,4,5}被认为是有用的特性。设B为一个大小W×W的块,hi(u)为DCT系数在第i个频率处的直方图,u在B中呈z字形排列。特征向量集由式(1)组成,通过上述方法获得每个样本9×11维的特征向量。

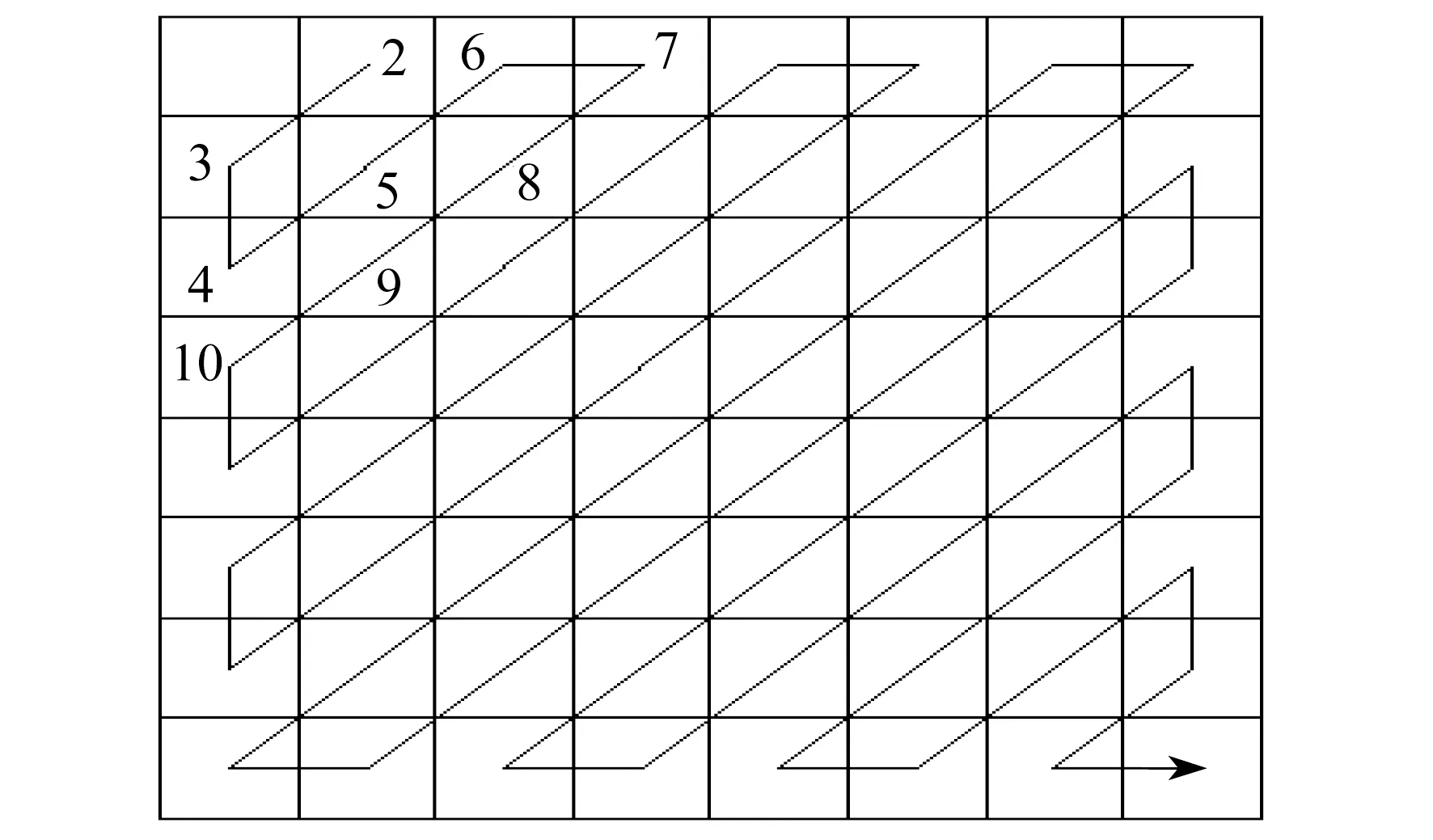
图2 Zig-zag取值示意

XB=[hi(-5),hi(-4),hi(-3),hi(-2),

hi(-1),hi(0),hi(1),hi(2),

hi(3),hi(4),hi(5)]

i∈2,3,4,…,10

(1)

2.2 网络设计

CNN依赖于3个概念:局部接受域、共享权重和空间子采样[15]。在每个卷积层中,输出特征图通常表示与多个输入的卷积,可以捕获相邻元素之间的局部依赖性。每个卷积连接之后都有一个池化层,池化层以局部最大化或平均的形式执行子采样,这样的子采样可以降低特征图的维数,进而降低输出的灵敏度[16]。在这些交替的卷积层和池化层之后,输出特征图经过几个全连接,然后输入到最终的分类层。分类层使用一个softmax连接来计算所有类的分布。

本文的CNN网络结构由2个卷积层、2个池化层连接和3个全连接层组成,如图3所示。

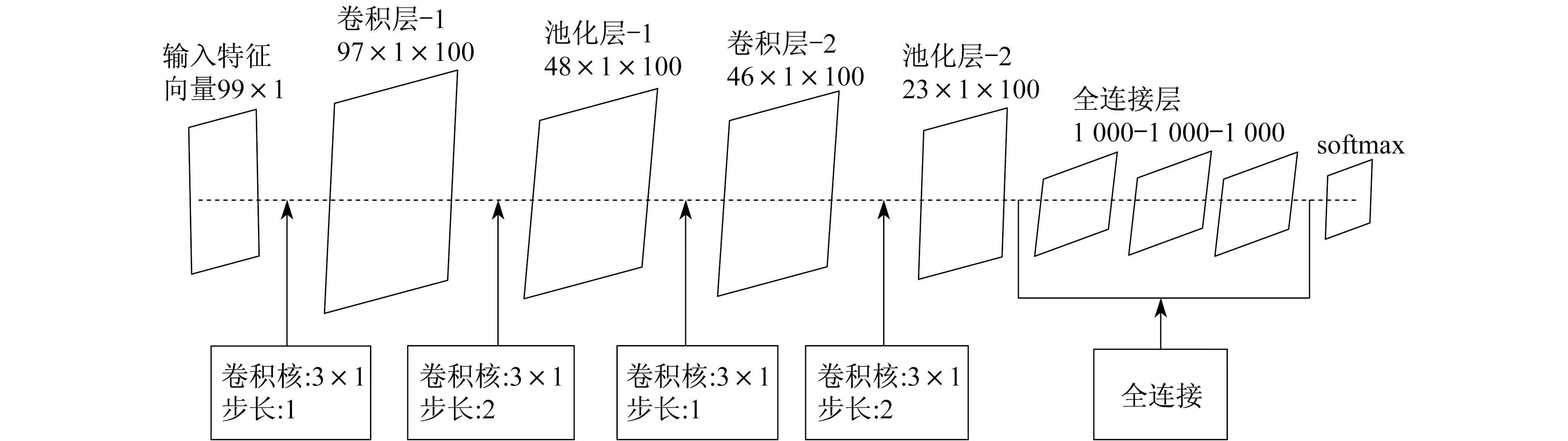
图3 CNN网络结构

输入数据为9×11维的向量,输出为两个类(单压缩/双压缩)概率的分布。对于卷积连接,将卷积核m×n设为3×1,卷积核数量k设为100,滑动步长设为1。以第1卷积层为例,输入数据的特征向量为99×1,第1卷积层将这些特征数据与100个3×1的卷积核进行卷积,步长为1。输出特征为97×1×100,即特征图数量为100,输出特征图维数为97×1。对于池化层,同样将卷积核m×n设置为3×1,池化步长设置为2,观察到这种重叠池化可以防止训练过程中的过拟合。每个全连接层有1 000个神经元,最后一个的输出与softmax层连接,可以产生出每个样本应该被分类到每个类的概率。在JPEG图像伪造检测中,只有单压缩和双压缩两类。

网络中每个连接层之间使用ReLU激活函数,激活函数为f(x)=max(0,x)。在文献[17]中,使用ReLU激活函数的深度学习网络收敛速度是传统学习网络的几倍,对大型数据库的训练性能效果更佳。在全连接层中,引入了“dropout”技术[18]。其核心思想是在训练过程中从神经网络中随机抽取单元,为有效地组合不同的网络结构提供一种方法。使用dropout技术,可以有效地缓解过拟合,缩短训练时间。

3 实验过程与结果分析

3.1 实验数据集

从Dresden Image Database图像数据库[19]中选取tiff格式的500张原始图像,70%进行训练,30%做测试,采用QF1为{60,70,80,90,95}进行第1次JPEG压缩,采用QF2为{60,65,70,75,80,85,90,95}进行第2次JPEG压缩,将产生5组共1 750张单压缩图片和40组共14 000张双压缩图片,图像块大小分别选择为64×64,128×128,256×256,512×512,1024×1024。实验环境为Python3.6,TensorFlow1.8.0.

3.2 实验结果与分析

设置不同的图像块大小,检测其在CNN网络中不同QF2时所检测分类的正确率,结果如表1所示。

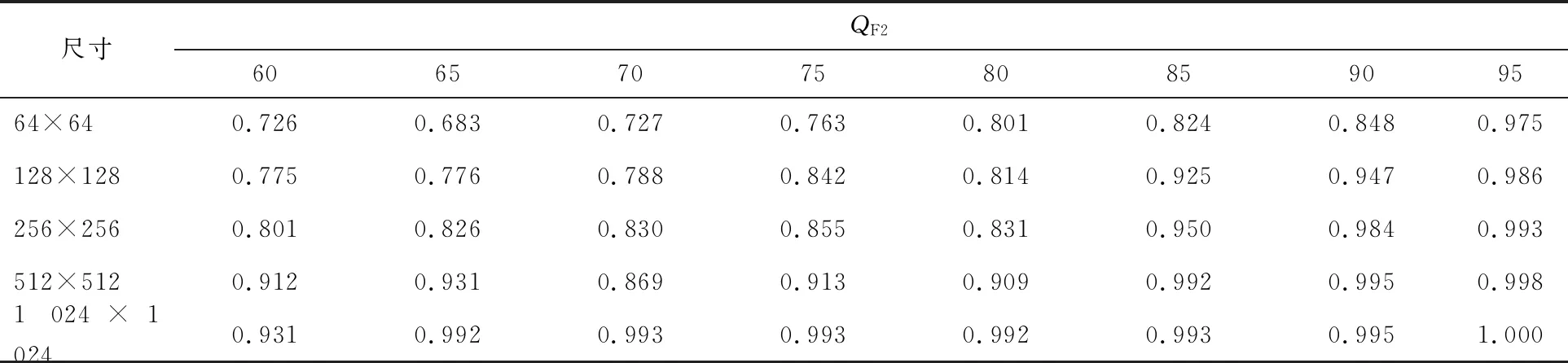
表1 采用本文算法时QF2在图像不同尺寸下检测的正确率

文献[20]使用DCT首位统计特征和SVM分类器相结合进行双JPEG压缩检测。本文中同样的样本在文献[20]算法中检测的正确率如表2所示。

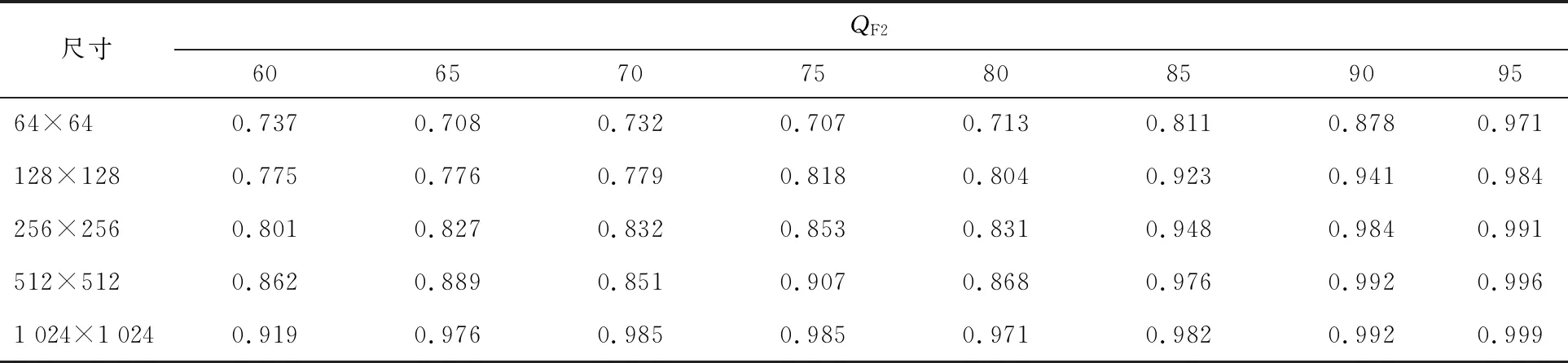
表2 采用文献[20]算法时QF2在图像不同尺寸下检测的正确率

为了直观地观察出表1和表2数值变化的趋势,将表1和表2数据分别生成图4和图5。

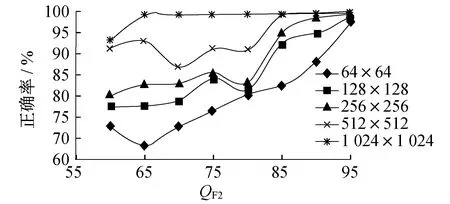
图4 采用本文算法时QF2在图像不同尺寸下检测的正确率

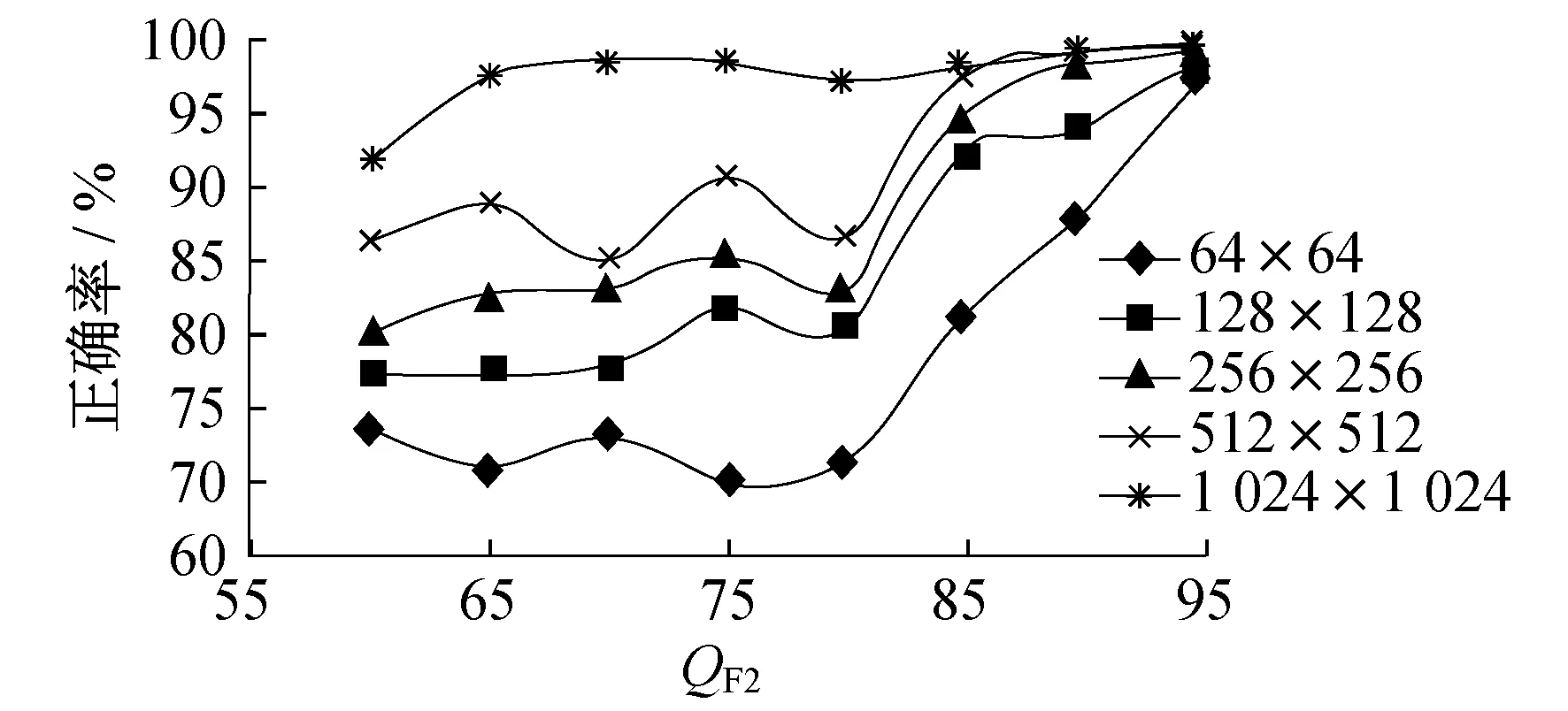
图5 采用文献[20]算法时QF2在图像不同尺寸下检测的正确率

由图4和图5可得出共同的结论:样本尺寸越大,分类检测的正确率越高;当样本尺寸大小为1 024×1 024时,正确率都非常高;本文提出的CNN算法性能明显优于文献[20]中的算法性能。首先,对于卷积神经网络,样本尺寸越大,所包含的统计信息越多,特征提取的也就越多,分类器越容易进行区分,所以检测正确率越高。其次,QF2值越大,分类器分类的正确率越高,当QF2为95时,检测正确率在最大尺寸下达到100%。当QF1

4 结 语

分析JPEG图像双压缩的特征可知,对于双JPEG压缩篡改检测而言,第二次压缩的直方图与第一次压缩的直方图不同,会出现很明显的周期值缺失或周期性极大值和极小值,因此本文提出了一种CNN对JPEG图像双压缩的检测算法。将图像的DCT系数直方图作为CNN网络的输入进行特征提取,利用深度学习可以用深层次网络自动学习到原始数据中隐含的关系,而不需要对数据进行“显式”的预处理。实验结果表明,与现有算法对比,本文提出的算法检测率最高提高了1.3%,证明了该方法在JPEG双压缩检测性能上的优越性。