最短时限指派问题的新决策方法
胡勇文,陈国华,刘 静
(1.湖北文理学院 机械工程学院;2.纯电动汽车动力系统设计与测试湖北省重点实验室,湖北 襄阳 441053)
0 引言
经典指派问题是运筹学中一个重要的组合优化问题,它在人员和运输调度、柔性制造系统中有广泛应用。该问题可描述为:n人要完成n项任务,由于每个人的专长不同,因此每个人完成各项任务的时间也不相同,问如何指派使得完成n项任务的总时间最少。实际生活中,n项任务通常同时开工,不但要求完成n项任务的总时间最少,还需要在最短时间内完成所有任务,即用时最多者达到最小。例如,手术室抢救病人过程中医护人员调度问题、救灾物资等调运问题、突发事故的抢修等问题均需要在最短时间内完成所有任务。一般将需要在最短时间内完成所有任务且总完成时间最少的指派问题称为最短时限指派问题,由于该类问题多数情况下符合实际需要,因此研究最短时限指派问题的决策方法具有重要意义。
最短时限问题首先由Gross[1]提出,并给出了改进圈的算法。此后,Garfinkel[2]借助求解最大流思想提出了一种求解最短时限指派问题的阀门算法,但该算法很难检验给出解的最优性。我国也有众多学者对最短时限指派问题进行了深入研究,求解最短时限指派问题的主要算法有:大M法[3]、逐步寻优算法[4]、生长树法及标号法[5]、借助二分图匹配思想的方法[6]、最短时限逼近法[7]及基于最小调整法思想的方法[8,9],其中文献[8,9]是较有代表性的方法。文献[9]是建立在匈牙利算法上的求解最短时限指派问题的算法,它需要通过变换矩阵,试指派,画最少零元素覆盖线等步骤,过程较复杂,也不利于计算机求解。文献[8]中方法对独立画圈元素没有预见性,仍需对问题先进行试指派,若试指派不满足行平衡及列平衡,需要进行修正步骤,且当问题的规模增大时,所需步骤较多,不利于计算机求解。
由于经典指派问题是特殊的最小费用流问题[10],熊德国等[11]提出了求解最小费用流的允许边算法,且该算法在求解稠密网络时具有良好性能[12]。鉴于最短时限指派问题的特殊性,本文通过计算确定最短时限值,构造最短时限指派问题的最小费用流模型,通过求解最小费用流模型的最优解而得到最短时限指派问题的最优解。
1 最短时限指派问题及其最小费用流模型
最短时限指派问题(Shortest Time Limited Assignment Problem,STL-A)的一般提法如下:假定n个人要完成n项任务,由于个人专长各异,不同人完成各任务所需的时间也不同。设指派第i个人去完成第 j项任务所需的时间为cij,所有任务均可同时开工,确定一个指派方案,使得在最短时间内完成所有任务,且所花时间和最少。令xij=0或1,当xij=1时表示指派第i人去完成第 j项任务,否则xij=0。则STL-A问题的数学模型如下:

最短时限的指派问题需先满足目标函数(1),即在目标函数(1)达到最优解的前提下,再使目标函数(2)达到最优。传统指派问题可建立如下形式的最小费用流模型(见图1)。

图1最短时限指派问题的最小费用流模型
其中集合M={1,2,…,n}表示n个人的集合,集合N={1′,2′,…,n′}表示n项任务的集合。此两组节点之间的边表示某人可以承担某项工作的对应关系,对∀i∈M,j∈N,边 (i,j)上单位流量费用cij对应STL-A问题中效率矩阵中元素cij,规定边(i,j)的容量uij=1,表示一人最多只能完成一项任务。对∀i∈M,规定csi=0,usi=1,表示一人最多完成一项任务;对∀i∈N,规定cjt=0,ujt=1,表示一项任务只能由一人完成。根据构造的传统指派问题的最小费用流模型有:传统指派问题等价于在图1中寻求从s至t的流量值为n的最小费用流。
假定问题STL-A的最优解为c*=minmax{cij|xij=1,i,j=1,2,…,n},则c*必为指派问题效率矩阵中的某一元素。此时最短时限指派问题STL-A可转化为以下单目标规划模型A:
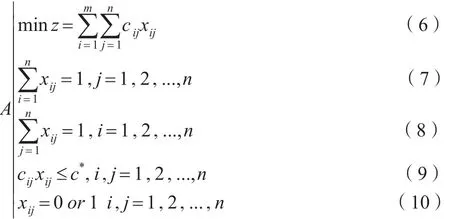
因此只要能确定c*,STL-A问题即可转化为经典指派问题。设cij为最短时限指派问题效率矩阵[cij]中第i行,第j列元素,i,j=1,2,…,n。若cij>c*,则传统指派问题的最小费用流模型中可令节点i到节点j的单位流量的费用为M,M为一无穷大的正数,表示在最短时限指派问题中,不能指派第i人完成第j项任务,否则STL-A问题的最优解大于c*。若cij≤c*,则在传统指派问题的最小费用流模型中节点i到节点j的单位流量的费用为cij。这样便得到STL-A的最小费用流模型。后文将介绍寻求STL-A问题的最优解c*的方法。
2 最小费用流模型的允许边算法
设经典指派问题对应的最小费用流问题的数学模型为:

为方便讨论,设所求的最小费用流问题对应的网络记为G=(N,A,U,C),其中N为节点集合,A为边集合,U为各边的容量集合,C为各边单位流量费用集合。则模型(11)对应的对偶问题为:

其中A为对应最小费用流网络中的边的集合,pi为对应节点i的对偶变量,pij为对应于边(i,j)的对偶变量,分别称为节点i及边(i,j)的势。设x={xij},p={pi,pij}分别为LP及DP的一组可行解,根据对偶理论的互补松弛定理,他们是最优解,当且仅当满足:

由于pi无约束,故可任意指定一组pi,并取:

则必有pij≤0,于是便得到DP的一个可行解。则式(13)可等价的写成:

最小费用流的允许边算法的基本思想为:从一个费用最小可行流(比如0流)开始,对其流量增广,在增广过程中始终满足条件式(15),便可得到一个流量更大的最小费用流,即在增广流量时,只有满足pi-pj=cij的边(i,j)上的流才允许调整。把满足pi-pj=cij的边(i,j)称为允许边,由允许边组成的网络称为允许网络,记为R。当允许网络中找不到可增广链且流量尚未达到原网络的最大流时,修改有关节点的势,以增加新的允许边构造新的允许网络,重新寻找允许网络中的可增广链,直到求得目标流。则求解指派问题的算法可描述为:
pi=0, ∀i∈N;xij=0,∀(i,j)∈A;给源点 s标号 (0,
第一步:①∀i∈S,
取:
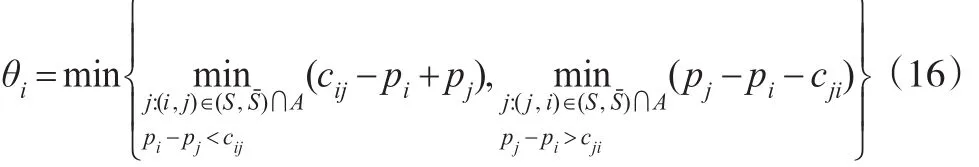

转②;否则,如不能确定θ,则当前流已为原网络的最大流,算法结束。

第二步:如果pi-pj=cij,则 (i,j)∈R;
第三步:①对i∈S,如 (i,j)∈R,j∈Sˉ,且xij<uij,则给j标号 (i,δj),其中;如(j,i)∈R,j∈Sˉ,且xij>0 ,则给j标号 (-i,δj),其中δj=
②如t∉S,此时,允许网络中达到最大流,转第一步;否则,如t∈S,则得到R中的一条可增广链μ,转③;
③增广流量
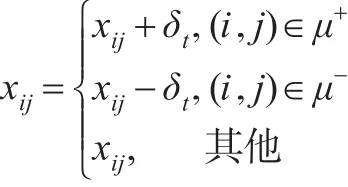
则流量变为:υ′=υ′+δt。如υ′=n,则已得到流量为n的最小费用流,算法结束;否则,保留源点s的标号,删除其余所有标号,转第三步①。
当最小费用流网络中未达到最大流,该算法通过增加及节点的势后总可以找到至少一条允许边,因此经过有限次数改变节点势后,必可找到一条从s至t的增广链。由于算法是在允许边上增广流量,暂且将此算法称作允许边算法。
3 STL-A问题的允许边算法
根据问题STL-A及A的关系,用最小费用流的允许边算法求解STL-A问题的基本思想为:先找出每行及每列元素中最小元素的最大者作为初始备选最优解,并在最小费用流网络中只保留效率矩阵中元素不大于初始最优解对应的边,并利用允许边算法寻求当前网络中的最小费用流,判断流量是否达到给定值。若流量未达到最优值,则以增值最小原则调整当前备选最优解,重复以上过程,直到在最小费用流网络中找到流量值为n的最小费用流,此时边xij=1,i=∈M,j∈N即为指派第i人完成第j项任务。
为寻求STL-A问题的最优解c*,令:

现考虑效率矩阵[cij]中位于不同行元素集C1={ci′j,i′=1,2,…,n} ,以及位于不同列的元素集C2={cij′,j′=1,2,…,n}。显然,对ci1j1,ci2j2∈C1,若有j1≠j2,∀i1,j1,i2,j2=1,2,…,n。则已找到STL-A问题的最优解,且xi′j=1 若ci′j∈C1;xi′j=0 ,若ci′j∉C1;同样,对ci3j3,ci4j4∈C2,有则已找到 STL-A 问题的最优解,且,若,若cij′∉C2。若不存在每行(列)中的最小元素位于不同列(行),即当前不存在STL-A的最优解。按照增值最小原则调整当前备选最优解,令:

实际上,T2对应在效率矩阵[cij]中值为T2的元素。此时在当前最小费用流网络中令:

其中,M为一无穷大的正数。
用允许边算法求解STL-A问题的具体步骤如下:初始化:
①按式(18)至式(20)计算T1。在对应的最小费用流模型中只保留cij≤T1的边。
②pi=0,∀i∈N;xij=0,∀(i,j)∈A;给源点s标号 (0,+∞);点S={s}∪M,Sˉ=N∪{t}。
此时流量υ′=0 。记割 [S,Sˉ]的前向边集为 (S,Sˉ),后向边集 (Sˉ,S):
第一步:①∀i∈S,

取:

转②;否则,如不能确定θ,则当前流已为原网络的最大流,即已找到STL-A问题的最优解,算法结束。
②并令:

第二步:如果pi-pj=cij,则 (i,j)∈R;
第三步:①对i∈S,如 (i,j)∈R,j∈Sˉ,且xij<uij,则给j标号 (i,δj),其中;如(j,i)∈R,j∈Sˉ,且xij>0 ,则给 j标号 (-i,δj),其中
②t∉S,此时,允许网络中达到最大流,转STEP1;否则,如t∈S,则找到R中的可增广链μ,转第三步③;否则,若t∉S,转第一步①;
③增广流量

则流量变为:υ′=υ′+δt。如υ′=n,则已得到流量为n的最小费用流,算法结束;否则,保留源点s的标号,删除其余所有标号,令T1=T1+min{cij-T1|cij>T1,i,j=1,2,…,n},并在当前最小费用流网络中增加值为T1的单位流量费用所对应的边,转第一步①。
根据以上算法描述,下面给出用允许边算法求解STL-A问题的正确性。
证明:对∀j∈N,若xjt=1,则t不能取得与j直接相关的标号;否则,由于cjt=0,若j能取得标号的同时,t也能取得标号,即找到一条从s至t的增广链。此外,对∀j∈N,若j能取得标号时,且xij=1,i∈M,则节点i也能取得标号。因此,第一次迭代后,至少找到一条增广链,流量增加量至少为1;在第l次迭代时,由以上讨论易知,通过更新T1的值,并在当前网络中加入对应的边后,最多经修改l次节点的势(l次迭代),便可寻求至少一条从s至t的增广链,流量至少增加1。因此,最多经1+2+…+n=(n2+n)/2次迭代后,即可得到流量值为n的最小费用流的最优解,此时节点s的势(此时ps=T1)即为满足时限最短要求的最优解,而边xij=1,i∈M,j∈N即为指派第i人完成第j项任务。
根据算法描述易知,本文的算法还适用于人数与任务数不相等、每人只能做一件事的最短时限指派问题,只需求解给定流量(流量值即为人数或任务数的值)下的最小费用流问题即可,且计算过程更为简单。针对一人可做多事或一事可由多人做的最短时限指派问题,只需调整边(s,i),i∈M或边 (j,t),j∈N的容量即可。如,第i#人可做两件事,则设定边 (s,i#)的容量为2,同理,若第j#可被两人做,则设定边 (j#,i)的容量为2。
4 算例
例1:某供电系统中有4处供电故障,该供电系统只有在所有故障均排除后才能恢复供电,现要分配4名工人到4处供电故障处检修。由于不同故障处所处条件以及各工人专长不同,不同工人检修不同的供电故障处的时间(单位:分)如表1。问如何指派4名工人,使得该供电系统在最短时间能恢复的前提下,总共检修时间最短。

表1 不同工人检修故障处所需时间表
该问题属于典型的最短时限指派问题,利用本文给出算法求解过程如下:
初始化:
按式(18)至式(20)计算T1,保留效率矩阵中元素值cij≤T1的元素,并建立对应的最小费用流模型,各边上的数据表示(cij,uij,xij)。为使图更加简洁,标号过程省略。且若边上流量为“0”,则该边的数据表示为(cij,uij),如图2。

图2初始化后的最小费用流模型
第一步:计算势θ,此时θ=min{15,18,18,17,16,17}=15。
第二步:寻求允许网络R中最大流。通过标号可找到一条增广链s→A→1→t,增广流量后,网络图如图3。由于此时流量值为1,未达到最大流量4,故仍需迭代。

图3允许网络R0上的最大流
第三步:经过三次迭代后,网络中的流量达到3,如图4,此时已达到初始化后最小费用流模型的最大流量,但未达到流量为4的最小费用流。故需更新T1,按式(21)规则更新后T1=19。加入对应边后的网络图如图5。

图4允许网络R上的最大流

图5更新T1后的最小费用流网络
第四步:经过两次迭代后,找到一条s→B→1→A→2→t的增广链,增广后的流量为4,已达到最大流,如图6。

图6T1=19时的最小费用最大流的最优解
图6中,网络中流量为4,已达到最大流。至此,对应表1中的指派问题的最优解为:工人A、B、C、D分别处理2、1、3、4处故障能使该供电系统在最短时间内恢复供电,并且总维修时间最少,最少总时间为18+19+16+17=70min。
5 结束语
本文将具有最短时限的指派问题转化为最小费用流模型,通过更新最短“时限”值而更新构造的最小费用流网络。同时利用基于对偶原理的允许边算法求解最短时限指派问题的最小费用流模型。与已有求解最短时限指派问题的算法相比,本算法不需要将最短时限指派问题通过矩阵反复变换转化为经典指派问题进行求解,而是通过计算最短时限值构造最小费用流网络,直接通过改变节点的势以扩大允许网络进而在允许网络中寻求最小费用流网络的最优解。该算法在迭代过程中充分利用了上一次迭代的信息,迭代过程简单,计算量小,易于在计算机上实现。

