基于动态规划的指派问题网络方法及其应用

鲍培文

（武警特警学院，北京昌平 102200）

指派问题是运筹学中的规划问题，主要是运用数学和现代计算机技术等科学技术方法，从数量方面揭示指派问题的模型、方法和应用，为科学地进行指派活动、合理利用资源、提高指派效益提供理论和方法.针对指派问题具有网络特征，设计基于动态规划的指派问题网络方法，有利于综合运用网络模型，解决指派问题.

1 指派问题及其网络方法

指派问题既属于资源优化的线性规划，又属于多阶段决策问题的动态规划.这也赋予指派问题的多种模型及求解方法，每一种模型和方法都有利于合理分配资源，提高有限资源的使用效益.

1.1 标准指派问题的网络化模型

在日常管理工作中，往往会碰到这样的人员分配问题：有 n项任务（或工作）A1，A2，…，An，需要给 n个人B1，B2，…，Bn去完成，每人只能执行一项任务.由于每个人完成每一项任务的时间（或效率）不尽相同，所以不同的分配方案完成任务的总时间（或总效率）也不同，要解决的问题是分配何人去完成何项任务，才能使完成n项任务的时间最少（或总效率最高）.

任务分配与工作指派问题简称为分配问题或指派问题（Assignment Problem）.指派问题的条件是：每项工作只能分配给一个单位（人）去完成；每个单位（人）只能接受其中一项任务.其中，工作数和单位数一致时，称为标准指派问题.非标准指派问题可以转变为标准指派问题[1]303-305.

标准指派问题的数学模型：（xij为第i项工作派第j个单位完成，f为总费用）

标准指派问题有很多种解法.笔者在《指派问题的等价问题研究》[2]中，介绍了指派问题的各种解法.随着网络方法的普及，可建立基于动态规划的指派问题网络化模型.即指派问题按任务划分为n个阶段，每一阶段初始状态xij，代表Ai到Bj保障小组的起始状态，规定x11=0，x（n+1）1=1，

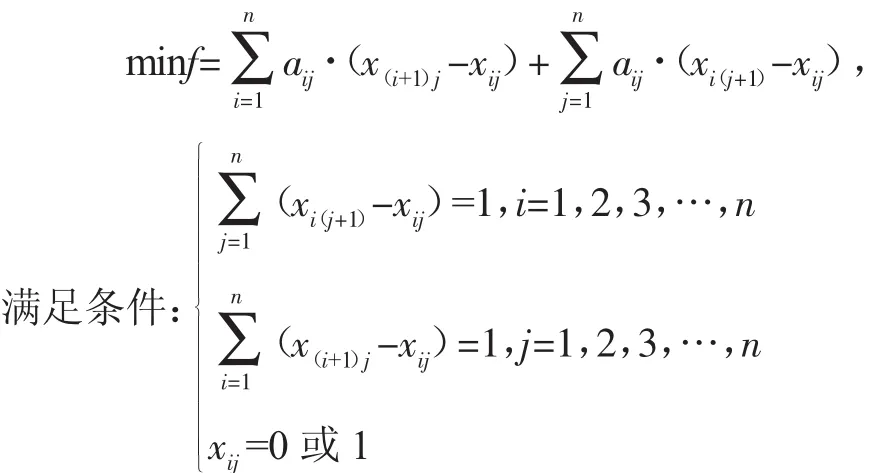
1.2 基于动态规划的指派问题网络方法

指派问题属于动态规划问题的特例.基于动态规划的指派问题，通过动态规划的建模方法，借用标号法求解最短路线思路，结合网络方法进行实例分析，进一步拓展指派问题解法[3].

网络方法可以从广义上和狭义上区分.广义上的网络方法，是把现代科学思想中网络的观点运用到指派问题中，不局限于内容.而狭义的网络方法，是指依托计算机网络和网络技术进行网络化计算.指派问题网络方法基于动态规划问题建立多阶段动态规划模型，采用标号法等方法，共同完成指派任务准备、任务实施和任务总结的完整过程.

1.3 标准指派问题网络方法流程图及算法

标准指派问题网络方法流程图（图1）从分析实际问题、列出时间矩阵开始，给出符合要求的可能分配方案，按照动态规划模型，使用网络方法计算每一分配方案的费用总值，寻找费用最小值.

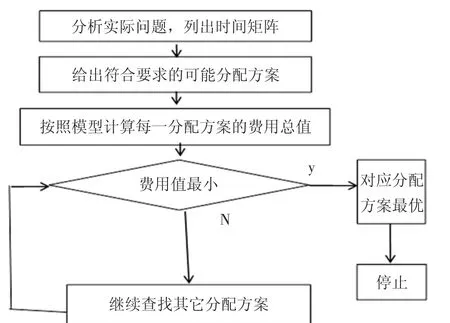
图1 指派问题网络方法流程图

指派问题网络方法lindo算法

model：

!n个工人，n个工作的分配问题；

sets：

workers/w1..wn/；

jobs/j1..jn/；

links（workers，jobs）：cost，volume；

endsets

!目标函数；

min=@sum（links：cost*volume）；

!每个工人只能有一份工作；

@for（workers（I）：

@sum（jobs（J）：volume（I，J））=1；

）；

!每份工作只能有一个工人；

@for（jobs（J）：

@sum（workers（I）：volume（I，J））=1；

）；

data：

cost=a11a12……a1n

a21a22……a2n

………………

an1an2…… ann；

enddata

end

2 基于动态规划指派问题网络方法的应用

基于动态规划指派问题网络方法，应用广泛而灵活.

问题 某修理所组成A1，A2，A3，A4四个修理小组，对B1，B2，B3，B4四个单位实施技术保障，由于各组的技术专长和设备不同，各单位的设备损坏程度不同，因此各组在各单位完成任务所需要的时间也不一样.假定具体时间如表1所示.问哪一修理组完成哪一个单位的技术保障任务，才能使总的时间最少.

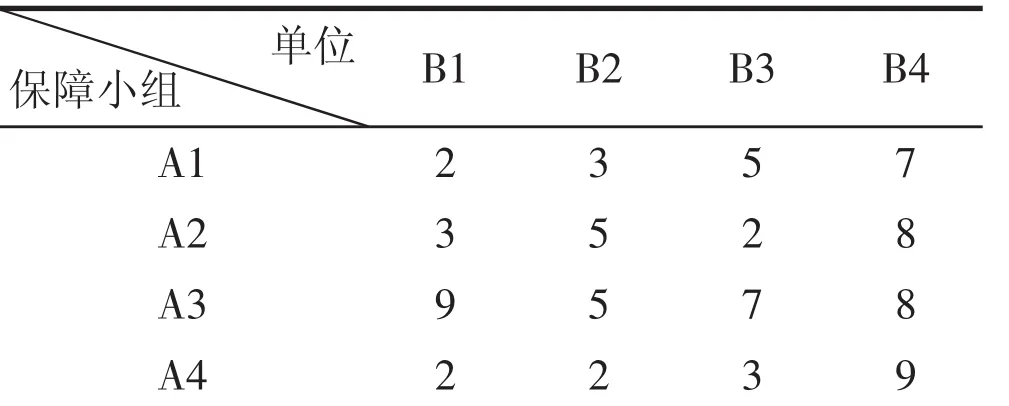
表1 修理组分配问题

这是线性规划的指派问题，建立指派问题模型：按任务划分为四个阶段，xij代表Ai到Bj保障小组的状态，规定xij=0，1状态为1表示派去，为0表示不派去，f为总的时间.

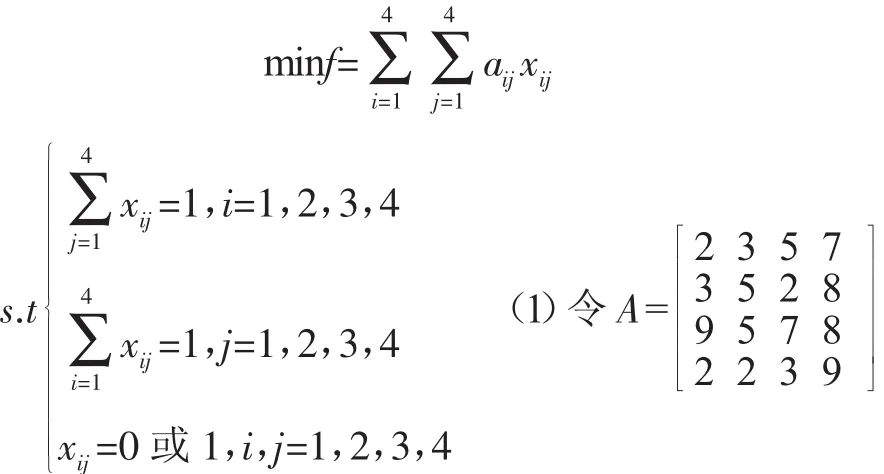
按照匈牙利法可以求出分配方案：A1到B1，A2到B3，A3到 B4，A4 到 B2.

下面按任务划分为四个阶段，每一阶段初始状态xij，代表 Ai到 Bj保障小组的起始状态，规定 x11=0，x51=1，

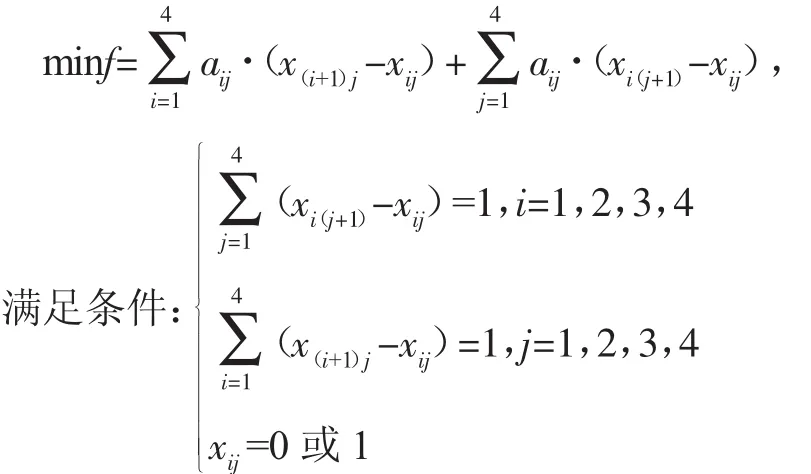
按照指派问题的模型、流程和算法，输出符合要求的指派方案，如图2和图3.

运行 lindo，分配方案，A1到 B1，A2到 B3，A3到B4，A4到 B2.

调用Python，结果如下：

#-*-coding：utf-8-*-

import numpyas np

import copy

c=[2，3，5，7，3，5，2，8，9，5，7，8，2，2，3，9

]

c=np.array（c）

c=c.reshape（（4，4））

all_p=[]

class obj：

def_init_（self）：

self.p=[]

self.cost=0

for i in range（4）：

for j in range（4）：

ifj==i：

continue

for u in range（4）：

ifu==i or u==j：

continue

for vin range（4）：

ifv==i or v==j or v==u：

continue

p=np.zeros（（4，4））

p[0，i]=p[1，j]=p[2，u]=p[3，v]=1

ans=obj（）

ans.p=copy.deepcopy（p）

ans.cost=sum（sum（c*ans.p））

all_p.append（ans）

all_p.sort（key=lambda ans：ans.cost，reverse=False）

print（all_p[0].p）

print（all_p[0].cost）

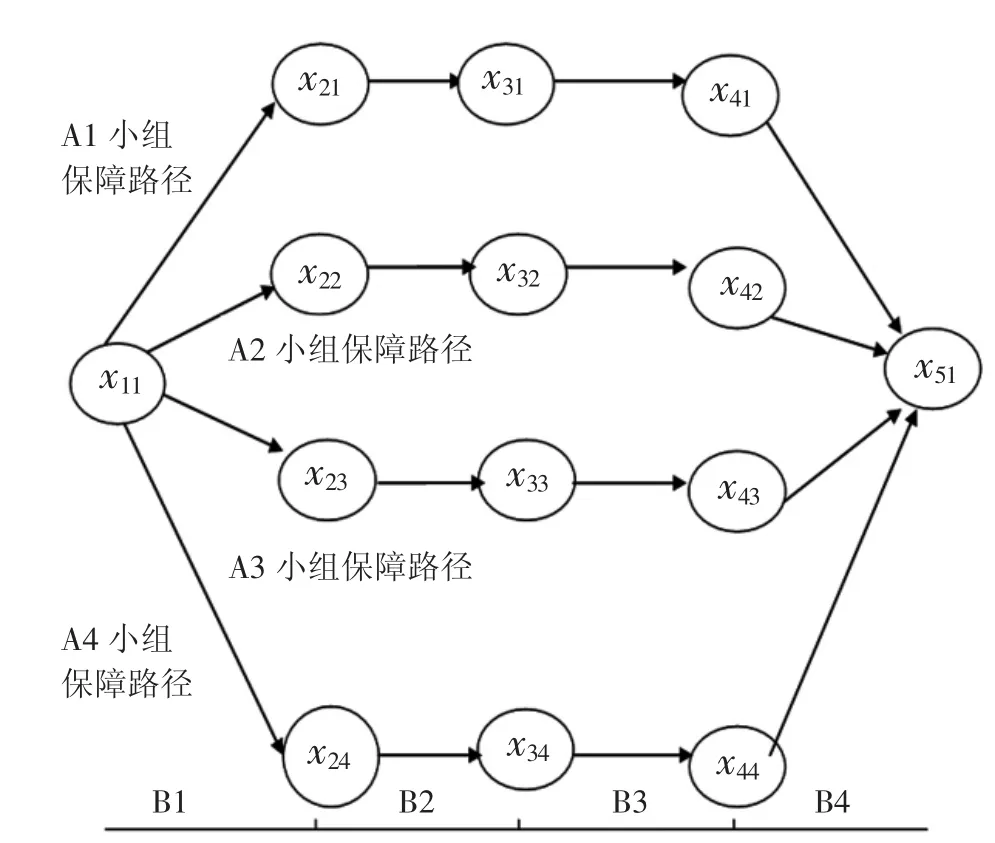
图2

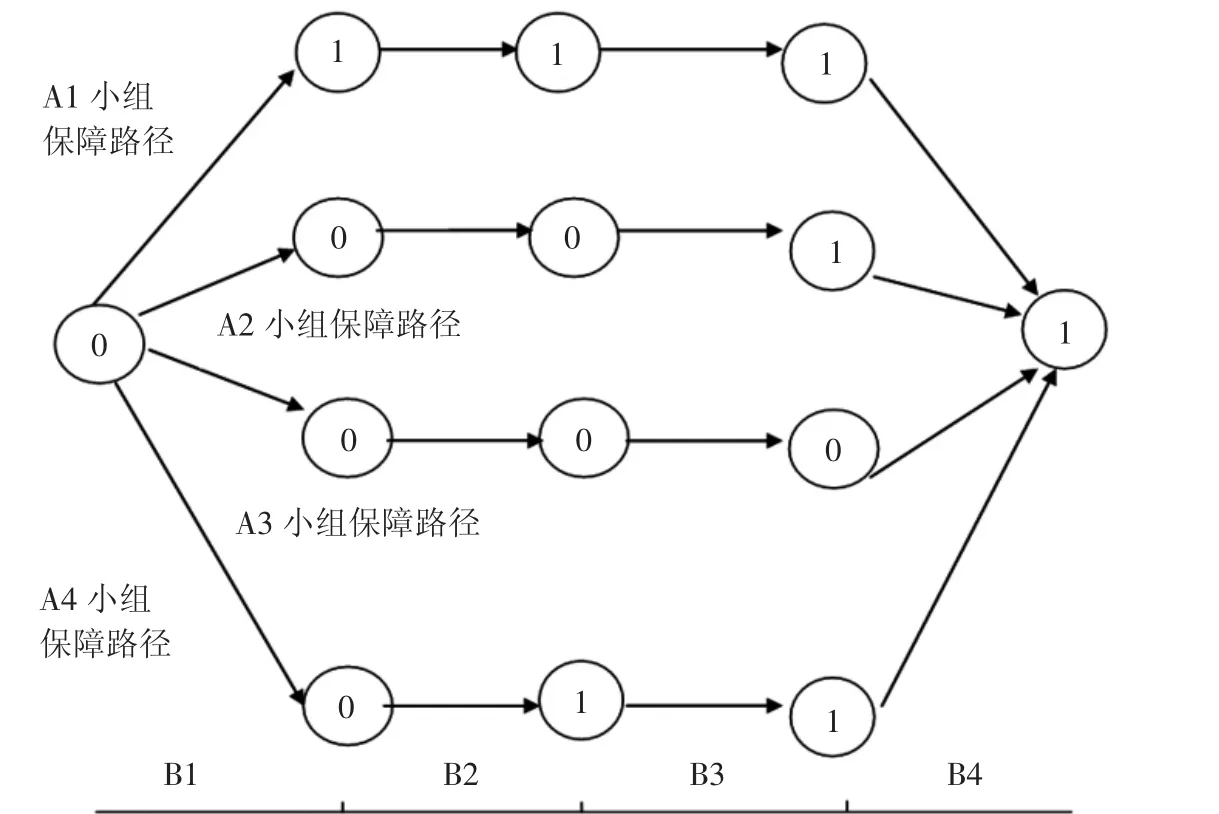
图3

Python 3.7.3（v3.7.3：ef4ec6ed12，Mar 25 2019，22：22：05）

[MSCv.1916 64 bit（AMD64）]on win32

Type“help”，“copyright”，“credits”or“license（）”for more

information.

＞＞＞

RESTART：C：/Users/Administrator/AppData/Local/Programs/

Python/Python37/33333333333.py

[[1.0.0.0.]

[0.0.1.0.]

[0.0.0.1.]

[0.1.0.0.]]

14.0

＞＞＞

3 基于动态规划指派问题网络方法应把握的问题

基于动态规划指派问题网络方法应注重理论联系实际，进行网络化分析，把握三对关系，提高决策优化能力.

3.1 整体与部分相统一.整体的各个部分是有机地、有组织地相互联系、相互作用着的，这种组织性使得各个部分所不具有的新特征和属性涌现出来；同时，部分在成为整体的成员后，作为部分所独有的特征和属性也会受到整体的限制和束缚.这就要求指派问题运用网络方法时，既为整体形成网络留出链路接口，提供参考，又使部分和整体内容相统一.

3.2 建模与网络方法相统一.指派问题网络方法关键步骤是根据问题建立模型，需要掌握一定的量化分析方法.量化分析方法并非人人都能掌握，给问题求解带来了难度.运用网络方法，可以突破难点，化难为易，收到意想不到的效果.如基于动态规划指派问题，模型的建立不是很好理解，但效仿最短路线法，用网络方法可以克服建模方法的困难，通过图上求解，还能辅助建模方法的进一步理解和掌握.

3.3 趣味性和互动性相统一.指派问题网络方法是模型的另一种形式，既拓宽了链路，又增强了互动性.在此网络方法中，看似无序，通过建模逐渐自组织为有序，形成网络结构实现多个属性、功能、行为，且具有相对的稳定性；条件变化又会影响和破坏网络的有序，就会进入下一个无序自组织、自学习，进而又成为有序.指派问题网络方法呈现网络模型的适应性、学习和自组织等特性，可以提高学习的兴趣，增强互动性.