基于直觉模糊熵的多属性决策方法

徐 颖，黄天民

(西南交通大学 数学学院，四川 成都 611756)

由于客观世界的复杂性和不确定性以及决策者对客观事物的认知程度等原因，传统的数学工具很难对问题进行准确的描述和刻画，也很难给出准确的结果.1965年，Zadeh[1-2]提出模糊集的概念，但其只用隶属度来度量模糊性，过于单一；1983年，Atanassov[3]在模糊集的基础上提出直觉模糊集，用隶属度和非隶属度来度量直觉模糊集的模糊性和不确定性.直觉模糊集与模糊集不同，直觉模糊集包含模糊数的隶属度、非隶属度以及犹豫度这三个方面的信息，在处理具有模糊性与不确定性信息的现实问题中更准确、更客观、更细致等，所以基于直觉模糊集理论的方法和应用，具有较好的实际意义[4-6].

笔者将直觉模糊集理论应用于多属性决策问题.在直觉模糊多属性决策问题中，属性权重的客观性会影响决策结果的客观性.于是，对属性权重的研究也至关重要.属性权重可以由专家直接给出，但其主观性太强.近年来，许多学者运用信息论中的熵来计算属性权重，能够较好地描述问题的不确定性，并且得出的属性权重具有客观性[7-11].本文也采用熵权法来确定属性权重.

文中提出一个新的直觉模糊熵，能够较好地解决一组直觉模糊集在隶属度和非隶属度相同以及犹豫度相同无法区分的情况，以及一些难以区分的情况.并将提出的直觉模糊熵应用于属性权重的求解，能够增加属性权重的客观性.给出决策步骤并应用于实例，说明该决策步骤的有效性及合理性.

1 预备知识

定义1[11]设X是一个非空集合，则称A={[xi,uA(xi),vA(xi)|xi∈X]}为直觉模糊集IFSs，其中uA(xi)和vA(xi)分别为X中元素xi关于A的隶属度和非隶属度，即uA:X→[0,1],xi∈X→uA(xi)∈[0,1];vA:X→[0,1],xi∈X→vA(xi)∈[0,1],且满足条件0≤uA(xi)+vA(xi)≤1.

定义2[11]设X中的任一直觉模糊集，若πA(xi)=1-uA(xi)-vA(xi),xi∈X,则称πA(xi)为元素xi属于A的犹豫度或者不确定度，显然0≤πA(xi)=1-uA(xi)-vA(xi)≤1,xi∈X.

定义3[11]设A={[xi,uA(xi),vA(xi)|xi∈X]}和B={[xi,uB(xi),vB(xi)|xi∈X]}为两个直觉模糊集，则运算法则如下：

1)A⊆B,当且仅当uA(xi)≤uB(xi),vA(xi)≥vB(xi),∀xi∈X;

2)A=B,当且仅当A⊆B和B⊆A;

3)A的补集AC={[xi,vA(xi),uA(xi)]|xi∈X}.

定义4[12]实值函数E:IFSs(X)→[0,1]称为直觉模糊熵，若满足如下公理化要求：

1)E(A)=0⟺A是分明集；

2)E(A)=1⟺uA(xi)=vA(xi)=0,∀xi∈X;

3)E(A)=E(AC);

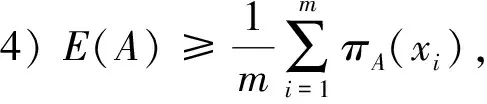
5)当πA(xi)=πB(xi)时，|uA(xi)-vA(xi)|≤|uB(xi)-vB(xi)|,∀xi∈X,或者当|uA(xi)-vA(xi)|=|uB(xi)-vB(xi)|时，πA(xi)≥πB(xi),∀xi∈X,则E(A)≥E(B).

2 改进直觉模糊熵的提出

目前所提出的直觉模糊熵存在的缺陷可以分为以下2类：

1)一类是没有考虑犹豫度对直觉模糊熵值的影响.如Zeng等[13]提出的直觉模糊熵：

2)另一类是考虑了犹豫度对直觉模糊熵值的影响.但某些情况不能够进行区分.如刘云生等[14]提出的直觉模糊熵：

王毅等[7]提出的直觉模糊熵：

高明美等[12]提出的直觉模糊熵：

以及赵飞等[10]提出的直觉模糊熵：

例2设A1={0.1,0.5,0.4},A2={0.2,0.5,0.3},A3={0.4,0.5,0.1},A4={0.3,0.4,0.3}为四个直觉模糊集，通过计算可得：

EG(A1)=0.5,EG(A2)=0.5,EG(A3)=0.5,EG(A4)=0.54;

EZ(A1)=0.586 7,EZ(A2)=0.622 7,EZ(A3)=0.823 1,EZ(A4)=0.698 8;

由此可知，EG(A)不能区分A1,A2,A3;EZ(A)虽然能够区分A1,A2,A3,A4,但是EZ(A3)>EZ(A4)=0.698 8,不符合直觉.

为了弥补以上直觉模糊熵的缺陷，提出一种改进的直觉模糊熵计算公式.对于任意的A={[xi,uA(xi),vA(xi)|xi∈X]}，定义：

(1)

通过计算可得:

例1E(A1)=0.75,E(A2)=0.5,E(A3)=0.65;

例2E(A1)=0.477 8,E(A2)=0.462 5,E(A3)=0.466 7,E(A4)=0.578 6;

于是可以弥补以上直觉模糊熵存在的缺陷.

定理1式(1)是直觉模糊熵.

证明只需证E(A)满足定义4中的1)～5)即可.

|uA(xi)-vA(xi)|≤|uB(xi)-vB(xi)|, ∀xi∈X,有

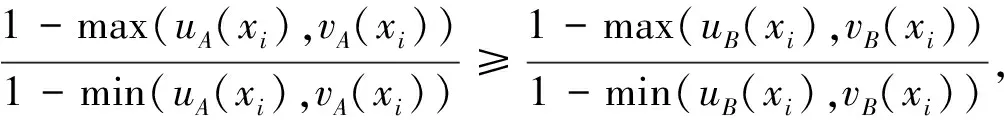
当|uA(xi)-vA(xi)|=|uB(xi)-vB(xi)|时，πA(xi)≥πB(xi),∀xi∈X,有

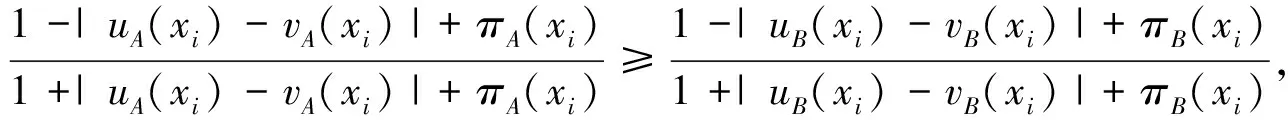
3 熵权法确定属性权重

本文利用直觉模糊熵来确定属性权重，即用熵权法确定属性权重，决策问题中的确定信息越多越有利于求解出属性权重，则直觉模糊熵越小.于是，可以建立如下的非线性规划模型：

构造Lagrange函数：

分别对wj和λ求偏导得：

解得：

(2)

由式(2)可知，某属性所包含的确定信息越多，即直觉模糊熵越小，属性权重越大，符合实际决策情况.

4 决策步骤及实例分析

决策步骤：

步骤1 对于给出的直觉模糊决策矩阵，由式(1)计算出各属性的直觉模糊熵；

步骤2 由式(2)计算出各属性权重；

步骤4 对各方案进行排序和择优.

例3 某房地产投资公司欲投资新建一处高端写字楼，通过行业分析需要考虑4个决策属性(都转化为同一类型的属性)A={a1,a2,a3,a4}，决策方案为U={x1,x2,x3,x4}，由专家给出的直觉模糊决策矩阵Y构造如下[8]：

a1a2a3a4

步骤1 计算得各属性的直觉模糊熵：E(a1)=0.419 8;E(a2)=0.225 7;E(a3)=0.370 7;E(a4)=0.544 1;

步骤2 计算得各属性权w1=0.246 7;w2=0.284 2;w3=0.258 3;w4=0.210 8;

步骤3 计算得各方案的综合得分函数值V(x1)=0.410 7;V(x2)=0.340 8;V(x3)=0.595 8;V(x4)=0.330 0;

步骤4 对各方案进行排序和择优：由V(x3)>V(x1)>V(x2)>V(x4)得x3>x1>x2>x4(“>”表示优于)，方案x3最优.

该决策步骤得出的各方案排序结果和文献[9]得出的排序结果一致，说明了该决策步骤的有效性.

5 结语

综合分析文献[7]、 [10]、 [12-14]所存在的缺陷，提出了一个新的直觉模糊熵，克服了文献中的缺陷.直觉模糊多属性决策问题中，存在属性权重未知的情况.为解决这类情况，需要从已知的数据信息中提取出相关信息来确定属性权重.本文利用直觉模糊熵来确定属性权重，有利于增加属性权重的客观性.给出的决策步骤运用于文献[9]中的实例，与文献[9]结果一致，但本文的决策步骤相对于文献[9]更为简单.但在公理化定义的规范化上，研究还不够深入，需进一步完善.