含参数“二次型”不等式恒成立问题的解法

江西省赣州市宁都中学 陈珊珊

二次函数是高中数学知识板块的重要组成部分，也是高考考查的一大热点。命题时多与其他知识交汇融合，特别是含参类不等式问题，一直是高考重点考查的题型。此类问题的求解常常需结合数形结合、分类讨论、化归与转化等思想方法，是高考的一大难点。“二次型”不等式恒成立问题一般都要转化为求函数的最值问题。下面从三个方面来介绍含参数的“二次型”不等式的解法。

一、判别式法

分析：解决此类问题的常规思路是，先对不等式的二次项系数a进行分类。当a=0时，是一元一次不等式；当a≠0时，是一元二次不等式。

解：（1）当a=0时，原不等式等价于-x-1≤0，解得x≥-1，此时不合题意，舍去；

评析：若所给变量x的取值范围为全体实数R，一般先对不等式中的参数进行分类：若转化为一次不等式，则肯定不满足；若是二次不等式，则依据开口方向和判别式同时判定，列出需要满足的条件，解不等式即可。

二、分离参数法

如果含参数的不等式中的参数和其余变量容易分离，那么常用方法是将参数放于不等式一边，其余变量整体放于不等式另一边，然后再研究含有其余变量的式子对应函数的最值，以此求得参数的取值范围。

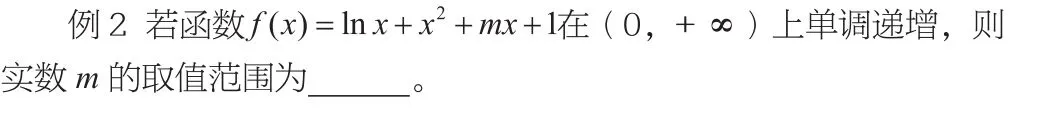
三、变换主元，构造新函数法

在很多的含参数二次不等式问题中，特别是当参数最高次是一次时，我们通常将函数变量字母与参数字母“地位”对调，将式子变形为以参数为新变量的不等式，将二次函数不等式转化为一次函数不等式来求解。

分析：这个不等式已知的是参数m的取值范围，反而是求“常规变量”x的取值范围，我们可以将不等式转化为关于m的“一次型”函数。那么把原来关于x的不等式恒成立问题等价转化为关于新变量m的一次不等式恒成立问题，则只需满足端点对应的函数值恒小于0。

从以上解法可以看出，一般含参类不等式恒成立问题的处理方法大都可以转化为函数的最值问题，这也是我们处理这类问题的常规思路。本文仅介绍了判别式法、分离参数法和变换主元，构造新函数法三种解答方法。实际上，另外还有数形结合法、函数性质法、整体代换法、反证法等多种解法，需要大家在平时的学习和练习中多归纳、多总结。