基于改进遗传算法的胎面生产线故障诊断方法

,

(武汉理工大学自动化学院, 湖北武汉430070)

世界轮胎工业[1]发展至今已有160多年的历史。作为汽车工业的上游行业，轮胎产业随着汽车工业的进步而持续发展。新车市场的扩张与汽车保有量的不断增加，为轮胎产业的发展提供了原动力。随着国家对轮胎需求的提升与轮胎产业集中度的持续提高，轮胎生产设备趋向于大型化、高速化、自动化和智能化，对各个生产环节的温度与电气控制指标的要求也越来越严格，因此，胎面生产线故障的有效诊断[2-4]与及时排除，对轮胎产业的发展有重大的意义。

布谷鸟搜索算法[5]是通过模拟布谷鸟的寄生育雏行为，有效地求解最优化问题的算法。该算法采用相关的列维飞行模式[6]搜索机制。研究表明，布谷鸟搜索算法比其他群体优化算法更有效。

遗传算法[7]是一种模拟生物进化的算法，它的基本观点是“适者生存”。遗传算法基于自然选择的原理，采用选择、交叉和变异等遗传算子来实现进化寻优。由于该算法具有潜在并行性、自适应、易于和其他算法相结合等优点[8]，因此往往也被应用于数据分类的问题中，并且与其他算法结合起来应用的效果更好。

针对轮胎胎面生产线故障诊断的问题，本文中提出一种用于分类问题的改进遗传算法。该算法调整遗传算法中初始种群的生成方法，避免了初始种群中包含无效个体；设计染色体的编码方法与适应度函数，可兼顾分类精度与规则集合复杂度2项指标；每隔若干代，将种群按适应度大小的顺序分为k类，在类间引入具有布谷鸟搜索思想的交叉算子，既可保持种群的多样性又加快了算法的收敛速度；最后，融入集成分类器设计思想，有效地利用了高维特征信息，以提高分辨性能。

1 用于分类问题的遗传算法

将遗传算法用于分类问题的本质就是找到一组能很好地拟合训练样例的IF - THEN规则[9]。算法中种群的进化过程可看作一个搜索过程,即在假设空间中搜索分类问题的最优规则。

1.1 染色体编码方法

本文中使用密歇根方法进行染色体编码。设特征向量X=(x1,x2,…,xk)，则每条染色体分为k个基因。整个种群表示一个规则集合。每条染色体表示一个完整的IF - THEN规则，种群中的各条规则互相竞争。每个基因分为3个部分，即权、运算符和值。特征属性对应特征基因，为规则中的IF部分；类属性对应类基因，为规则中的THEN部分。本文中使用的染色体编码方法如图1所示。

图1 染色体编码方法示意图

权表示该基因是否在规则中出现：0表示忽略该基因；1表示该基因会在规则中出现。运算符表示对特征值所采取的操作符：若是离散属性,使用符号等于或不等于；若是连续属性,使用符号大于或小于等于。值表示基因中操作符的合取项：若是离散属性,值等于实际值在取值域中的位置；若是连续属性,值等于实际值。

1.2 种群的初始化

在传统的遗传算法中，初始种群的生成方法为：随机产生n个初始串结构数据，每个串结构数据称为一个个体，n个个体构成初始种群。由于这种方法可能会产生很多无效个体(指染色体代表的规则没有可行解)，因此，本文中设计了一种种群初始化方法。该方法既可避免初始种群产生无效个体，又可避免初始种群距离最优解太近或者太远，使结果停留在局部最优。

设每条染色体中包含k个基因，任意类别中每个基因值的上、下界是已知的。设第i类中第j个基因值的上、下界分别为xj0和xj1，则xj1可以看作xj0的补集。设类别数为m，对m类分别进行初始种群的生成操作，其中每类中生成2k-1条染色体，初始种群中包含2k-1m条染色体。

为了便于表达种群初始化方法， 以下以m=2，k=4为例，得到如图2所示的种群初始化模型。

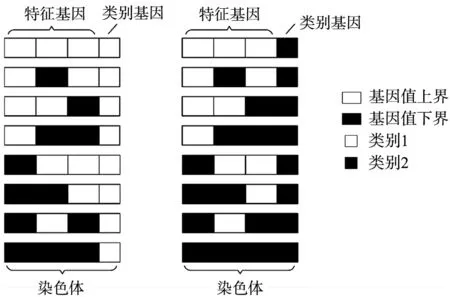
图2 种群初始化模型示意图

1.3 适应度函数设计

在设计适应度函数时考虑以下3个因素：

1)分类精度。设计适应度函数的一个重要指标是规则在训练样本上的分类精度。描述不能被正确分类的训练样例信息定义为

e=log2t+(w+u)(log2t+log2m)

(1)

式中：e表示该条规则在训练样本上的错误率，e越小，该条规则的正确率越高；t表示样本总数；w表示错判样本数；u表示不能做出判断的样本数。

2)样本间距离。考虑到不同类的样本分布在空间的不同位置，彼此之间的距离较远；而同一类的样本往往在空间中聚集在一起，因此在设计适应度函数时还考虑了样本间的距离这一因素。样本间的距离定义为

(2)

式中：d表示样本间的聚类属性值，d越小，样本属于同一类的可能性越大；k表示训练样本的特征数；xjp表示样本集中第j个样本的第p个特征值；yjip表示样本集中第i类中第j个样本的第p个特征值。

3)规则集合复杂度。如果不考虑规则集合复杂度，可能会导致规则集合过于复杂，没有普遍的适应性，也就丧失了分类的初衷。为了使算法挖掘出的规则既有较高的准确率，又较为简洁，具有良好的代表性，描述规则简洁程度的量定义为

l=log2vj+1+hjlog2vj

(3)

式中：l表示该条规则的简洁程度，l越小，规则越简单；vj表示属性j的取值个数；hj表示属性j编码位串中的模拟区间个数。

对于上述3个因素分别赋予不同的权值a、b、c，则适应度函数f定义为

f=ae+bd+cl

(4)

参数的确定过程如下：

1)对于参数a和b，满足a≥0，b≥0且a+b=1。对于相同的数据集，参数a、b的设置不同，分类效果也不同。在实际问题中，可在实验中确定较优的a、b参数值。

2)参数c在算法执行过程中并不固定。在算法迭代次数较少时，参数c取较大值，以尽可能多地挖掘出样本规则；当数次迭代都没有新规则产生时，随着迭代的进行减小参数c，提高结果的泛化能力。为了调整参数c，引入初始速率的复杂性I、最大延迟M、权重松弛因子W这3个变量。参数c的初始值设定公式为

(5)

式中r表示当前染色体数。 在后续的种群进化过程中每经M代染色体数目未发生变化， 就将系数c与权重松弛因子W相乘。 经实验， 上述3个变量的一种比较稳定的参数设定为0.075、 10、 0.9。

1.4 交叉操作

遗传算法运行速度较慢， 效率很低， 并且在处理大规模数据时容易陷入局部最优。 为了加快算法的收敛速度， 提升算法性能， 本文中采用了融入布谷鸟搜索思想的遗传算法交叉算子， 即每隔若干代， 将种群按照适应度的顺序分为若干个类别， 记录每个类别中适应度值最小的个体， 把它看作“最优的窝”,让其他类别中的布谷鸟按照一定的速度向每个类中的“最优的窝”靠近， 即进行交叉操作。 交叉概率体现了布谷鸟的靠近速度。 交叉算子共分为3种。

1)类间交叉。随机选择某一类别中的最优染色体与另一类别的最优染色体进行交叉操作。

2)布谷鸟搜索交叉。使用布谷鸟搜索算法选择出每个类别中的最优染色体与另一类别的其他染色体进行交叉操作。

3)类内交叉。在同一类别中随机选择2个染色体进行交叉操作。

本文中使用的交叉算子为单基因交叉算子，每次只互换染色体中的某一个基因，这样就避免了大规模的基因交叉破坏规则结构，防止了无效个体的产生。

1.5 复制与变异操作

本文中的复制与变异操作采用精英保留策略。

在本文算法中，将保留每一代种群中最优的2个个体不参加变异。对种群中的其他个体按变异概率进行变异操作。另外，因为个体编码方式与传统遗传算法不同，所以本文中的变异算子包括3种类型，即权变异、运算符变异与值变异。

1)权变异。发生变异基因的原权值为0，则变异为1；原权值为1，则变异为0。

2)运算符变异。发生变异基因的原运算符为等于，则变异为不等于；原运算符为不等于，则变异为等于；原运算符为大于，则变异为小于等于；原运算符为小于等于，则变异为大于。

3)值变异。在属性的取值域中随机选取一个值代替发生变异基因的值。

1.6 集成分类器设计思想

集成分类器可以在一定程度上提升分类性能[10]， 且基分类器的多样性越强， 分类稳定性越好， 因此本文中采用了一种基于特征选择集成分类的思想对分类器进行设计。 对于目标规模为m的多分类器， 转化为m个基于特征选择的二分类器。

基分类器设计完成后，得到m个基分类器分别为{s1,s2, …,sm}。在实际分类问题中，若有样本满足2个以上分类器的分类规则，则选择其中差异度较大的分类器。基分类器i与基分类器j之间的特征区分度Tij定义为

(6)

式中si与sj分别表示第i个分类器与第j个分类器的规则集合确定的分类区间。

当存在着多个差异度相同的基分类器时，对集成分类器的分类决策采用投票方法进行表决。第n个样本在第m个二分类器上的决策函数fnm定义为

(7)

则对个数为m的基分类器，第n个样本的决策fn定义为

fn=fn1⨁fn2⨁…⨁fnm

(8)

用于分类问题的改进遗传算法的流程如图3所示。

2 常用数据集的实验与分析

为了验证算法的性能，本文中选取了机器学习数据库的3个常用数据集进行实验，数据集具体信息如表1所示。

实验随机选取数据集的70%作为训练集，余下30%作为测试集。

为了验证改进遗传算法的有效性，本文中对每个数据集分别采用经典遗传算法、 仅使用本文初始种群生成方法的经典遗传算法和改进遗传算法进行仿真实验，每项实验均重复10次。

其中Iris数据集类别数量为3，分别为山鸢尾、杂色鸢尾、维吉尼亚鸢尾，记为类别1、2、3。特征属性数量为4，分别为花萼长度、花萼宽度、花瓣长度、花瓣宽度。使用改进遗传算法对Iris数据集进行10次仿真试验后，得到的最优规则集如表2所示。

图3 用于分类问题的改进遗传算法流程图

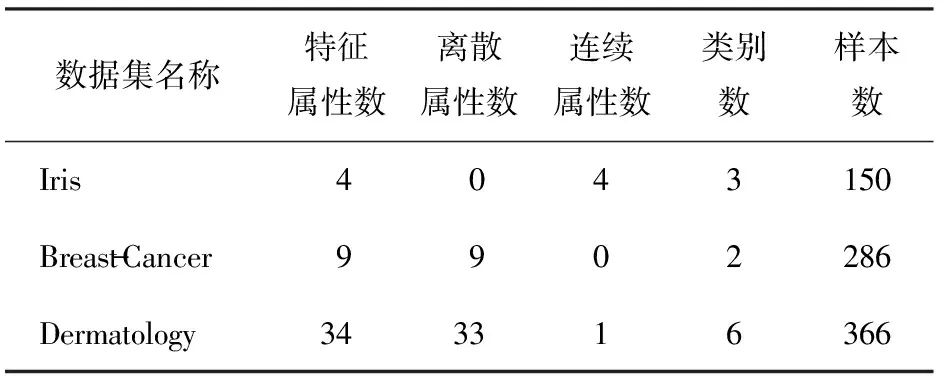
表1 实验使用的数据集信息表

表2 Iris数据集最优规则集

Iris数据集测试样本上3种算法的正确率分析如表3所示。各算法在实验使用的3个数据集测试样本上的平均分类准确率如表4所示。改进遗传算法对不同适应度函数权重系数的分类准确率见表5。

表3 Iris数据集测试样本数为15时的正确率分析

表4 3种算法的平均分类准确率

表5 改进遗传算法对不同适应度函数权重系数的分类准确率

由实验结果可得如下结论：

1)经典遗传算法算法相较于另外2种算法，最差情况与最优情况的差别较大，说明随机产生初始种群很可能会出现无效个体，不具有现实意义，且容易陷入局部最优。而使用本文中的初始种群选择方法可以有效克服该缺点。

2)改进遗传算法的分类效果优于另外2种算法，原因是改进遗传算法的收敛效果更佳，算法中的类别间交叉操作使得种群在多个不同区域同时进化。改进遗传算法在保持种群多样性的同时提高了收敛速度。

3)改进遗传算法在Iris数据集上的分类准确率依次低于Dermatology数据集与Breast - Cancer数据集。Iris数据集中特征属性为连续值，Dermatology数据集中特征属性部分为离散值，部分为连续值，而Breast - Cancer数据集中特征属性全部为离散值。这说明遗传算法分类器比较擅长特征属性为离散的数据分类。实验中还发现，适应度函数权重系数的不同对分类结果也有影响：提高参数a的值可以提高Breast - Cancer数据集与Dermatology数据集的分类准确率；提高参数b的值可以提高Iris数据集的分类准确率。由此可知，对于特征属性为离散值的数据集，可以适当增大参数a的值以提升分类效果，对于特征属性为连续的数据集，可以适当增大参数b的值以提升分类效果。在应用中应按照实际情况选择合适的适应度函数权重系数。

3 胎面生产线实例分析

胎面挤出联动生产线是以挤出机为主要装置，包含密炼、敷贴、硫化、纵裁和质量检查等设备的大型生产线。

调试专家依据生产线中某型挤出机的机头转速、压力、主机电流对历史数据进行了故障分类，分为正常情况与3种故障类型，分别为：类型0——正常情况；类型1——双螺杆的止推轴承润滑不够；类型2——2根螺杆之间的间隙出现了严重偏差；类型3——机头杂质过多，机头压力不稳定。本文中选择该型挤出机4种类别样本各18个共72组数据作为训练样本，该型4种类别样本各7个共28组数据作为测试样本，进行仿真分析。部分样本数据及类型如表6所示。

使用改进遗传算法对样本数据进行10次仿真试验，得到最优规则集如表7所示(a=0.25，b=0.75)。

实验结果表明：改进遗传算法可以很好地实现胎面挤出联动生产线的故障诊断工作，并得到了各种故障类型的最优规则集。在生产线控制系统出现故障时，工作人员可以直接根据设备仪表的显示数对故障类型进行初步鉴别， 从而减小故障发生对产品生产带来的影响，这也是该分类算法优于其他算法的地方。

表6 胎面生产线部分数据样本

4 结语

故障诊断技术是一门多领域交叉性学科，需要综合应用许多新兴的理论与技术,在故障诊断领域，仍有很多的想法有待于进一步的研究与实现。同样，本文中还存在着很多有待完善的地方：

1)遗传算法分类器对于特征属性一部分是离散的而另一部分连续的数据集，适应度函数的权重系数应怎样调整才能效果最佳，仍存在着疑问。

2)实验中发现，并不是适应度越低的染色体价值就越大，还存在某些适应度较高的染色体能提升分类效果。 对于比较简单的数据集， 可以人为地选择较多的优秀染色体，删除重复规则，得到最优的分类结果，但是对于复杂的数据集，如何准确地挖掘出这些染色体，仍有待于进一步的研究。

表7 胎面生产线数据样本最优规则集