一类非线性耦合梁方程解的动力学行为

，

(太原理工大学数学学院， 山西太原030024)

梁方程是一种常见的偏微分方程，有关其解的性质及吸引子的存在性一直是研究热点。文献[1]中提出了一类振动梁模型，文献[2-4]中对此类方程进行定性的分析，证明了该问题解的存在唯一性，考虑到影响材料的各种因素，文献[5-8]中建立了更广泛的梁方程，并进行了较深入的研究，即考虑该类方程整体吸引子的存在性。近年来，许多学者对耦合梁方程不同类型的吸引子展开了进一步讨论[9-13]。

本文中在已有研究的基础上，考虑方程

(1)

初始条件为

(2)

边界条件为

(3)

式中：u=u(x,t)为点x在时刻t的位移；θ=θ(x,t)为点x在时刻t的温度； Δ为拉普拉斯算子； Δ2u为u对x求四阶偏导数；为梯度算子；ut、utt分别为u对t求一阶、 二阶偏导数；θt为θ对t求一阶偏导数；f1(· )、f2(· )为非线性函数；h=h(x)∈L2(Ω), (L2(Ω)为Ω上实值Lebesgue可测函数全体)，Ω=[0,L](L为梁的长度)为实数集中的有界区域；p∈,α,β,γ>0。本文中利用Hölder不等式、Young不等式并结合分部积分法来证明方程(1)存在整体吸引子；在证明方程(1)存在有界吸收集时，大多学者利用Nakao引理化成有关非负连续函数上确界的不等式，过程较繁琐，本文中不需要化成以上形式即可证明方程(1)存在有界吸收集。

1 预备知识

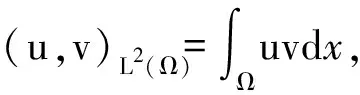
假设1f1∈C1()(C1()为上一次连续可微函数全体)，∃k0>0,ρ>0， 使得并记其中为函数f1(s)对s求一阶导数，λ1>0为Δ2在的第一特征值。

假设2f2∈C1(),对∀,存在常数k1、k2,且ρ≥0有

引理1[14-15]有界集B0⊂H是半群S(t)的一个有界吸收集， 如果对任一有界集B⊂H， 存在tB=t(B)≥0, 有S(t)B⊂B0, ∀t≥tB。

引理2[14-15]设∀B∈H是有界正向不变集,对∀ε>0, ∃T=T(ε,B),有

这里φT∶H×H→R对∀zn⊂B,满足

则半群S(t)在H是渐近紧的。

引理3[14-15]S(t)是定义在H上的一个耗散半群，S(t)存在紧吸引子当且仅当S(t)在H中渐近光滑。

2 解的存在唯一性

利用Galerkin方法及Gronwall引理可得如下结论。

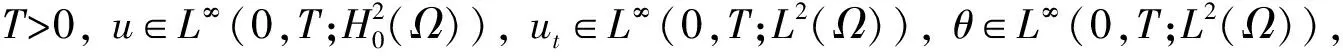
由定理1可定义H上的C0半群{S(t)}t≥0，即S(t) ∶H→H，也即S(t) ∶ (u0,u1,θ0)→(u,ut,θ)。

3 整体吸引子

定理2 如果假设1、 2成立，则问题(1)—(3)在H中存在有界吸收集B0。

证明：令v=ut+δu(δ为正常数)，则方程(1)的第1个等式可化为

f1(u)+αΔθ=h(x) 。

(4)

式(4)与v作内积，方程(1)的第2个等式与θ作内积，并将2个式子相加有

α(Δθ,v)-α(Δut,θ)=0。

(5)

由于

因此结合式(5)，令

(7)

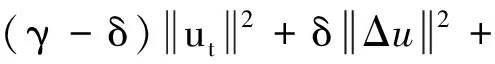
(8)

则式(5)可改写为

(9)

由假设1及Young不等式可知

(10)

(11)

由假设1、 2，有

(12)

(13)

将式(12)、(13)代入式(8)有

(14)

(15)

显然

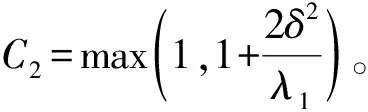
结合式(11)、(15)、(16)，将式(9)在[0,t]上积分可得

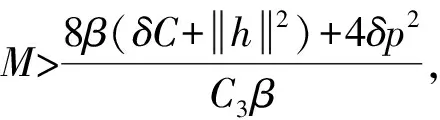
需要说明的是， 大多学者利用Nakao引理证明有界吸收集， 过程比较复杂， 本文中主要利用Hölder不等式、 Young不等式证明有界吸收集， 方法较简单。

定理3 如果假设1、 2成立，则问题(1)—(3)的半群{S(t)}t≥0在H中渐近紧。

证明：取初值(u0,u1,θ10), (v0,v1,θ20)∈H, (u,ut,θ1)、 (v,vt,θ2)为问题(1)—(3)的2个解，令w=u-v,ζ=θ1-θ2,满足下列方程

(17)

令z=wt+δw，将方程(17)的第1个式子与z作内积，第2个式子与ξ作内积，2个式子相加，有

(αΔξ,z)-(αΔwt,ξ) =0。

(18)

(19)

由假设1、 假设2、 Hölder不等式可得

(20)

(21)

类似式(13)，有

(αΔξ,z) -(αΔwt,ξ) ≥

(22)

(23)

其中c1为L2(ρ+1)(Ω)嵌入到L2(Ω)的嵌入常数,即

(24)

综合式(19)—(24)代入式(18)有

(25)

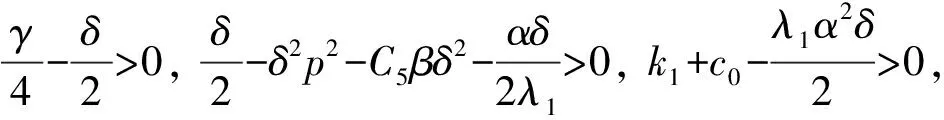
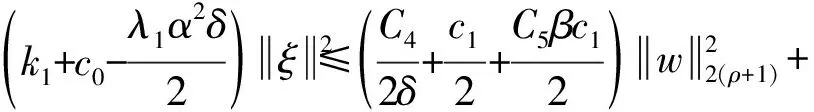
(26)

式(26)可简记为

(27)

由Gronwall引理可得

Ew(t) ≤Ew(0)e-C′t+

(28)

因此有

(29)

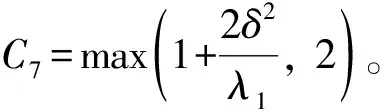
再根据Galiardo-Nirenberg插值不等式有

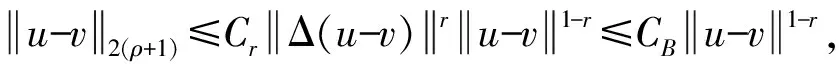
即

因此

定义

φT((u0,u1,θ10), (v0,v1,θ20))=

则有

ε+φT((u0,u1,θ10), (v0,v1,θ20))。

即

由引理2可知，半群{S(t)}t≥0在H中渐近紧。定理3证毕。

由定理2、定理3及引理3可知，半群{S(t)t≥0}在H中存在整体吸引子。

4 结论

本文中证明了一类非线性耦合梁方程解的存在唯一性和整体吸引子的存在性，为梁方程解的合理的Galerkin截断提供了理论依据，也为实际工程提供了设计依据。进一步的研究可考虑整体吸引子是否具有有限的Hausdorff维数。